Неоднородная марковская цепь

В общем случае вероятности переходов могут меняться от шага к шагу. Марковская цепь, обладающая таким свойством, называется неоднородной.

Обозначим через вероятность перехода системы из состояния  в состояние на k-м шаге. Каждому шагу соответствует своя матрица переходных вероятностей :

.

Вероятность того, что система после k-го шага окажется в состоянии выражается формулой

или в матричной форме

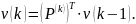
Пример. Производится три выстрела по цели, которая может быть в тех же четырех состояниях, что и в предыдущем примере, но вероятности переходов для трех последовательных выстрелов различны и заданы тремя матрицами:

В начальный момент цель находится в состоянии S₁. Необходимо определить вероятности состояний цели после 3 выстрелов.

Решение:

Сумма элементов вектора вероятностей состояний на любом шаге равна единице.

Таким образом, вероятности состояний цели после 3 выстрелов:

• цель невредима: ;

• цель незначительно повреждена: ;

• цель получила существенные повреждения: ;

• цель полностью повреждена и не может функционировать: .

Марковские случайные процессы с дискретными состояниями и непрерывным временем. Уравнения Колмогорова для вероятностей состояний.

Выше рассматривалась марковская цепь, т.е. случайный процесс, протекающий в системе, которая может переходить из состояния в состояние только в некоторые, заранее определенные, фиксированные моменты времени.

На практике значительно чаще встречаются ситуации, когда переходы системы из состояния в состояние происходят не в фиксированные, а в случайные моменты времени, которые заранее указать невозможно – переход может осуществиться в любой момент. (Например, выход из строя любого элемента аппаратуры может произойти в любой момент времени.)

Для описания таких процессов может быть применен аппарат марковских случайных процессов с дискретными состояниями и непрерывным временем, называемых также непрерывными марковскими цепями.

Рассмотрим, как выражаются вероятности состояний для такого процесса. Пусть имеется ряд дискретных состояний:

S₁, S₂, …, S_n,

причем переход системы S из состояния в состояние может осуществляться в любой момент времени. Обозначим через вероятность того, что в момент t система S будет находиться в состоянии S_i (i = 1, …, n). Очевидно, что в любой момент времени t сумма вероятностей состояний равна единице:

так как события, состоящие в том, что в момент t система находится в состояниx S₁, S₂, …, S_n, несовместны и образуют полную группу событий.

Основная задача при исследовании непрерывных марковских цепей: определить вероятности состояний для любого момента времени t.

В случае марковских процессов с дискретным временем для расчета вероятностей состояний необходимо знать переходные вероятности , определяющие вероятности перехода системы из состояния в состояние в точно заданный момент времени. Но для непрерывной марковской цепи вероятность перехода в точно заданный момент времени будет равна нулю (точно так же, как вероятность любого конкретного значения непрерывной случайной величины). Поэтому вместо переходных вероятностей для непрерывных марковских цепей используются плотности вероятностей перехода .

Пусть система S в момент времени t находится в состоянии S_i. Рассмотрим малый промежуток времени Δt, примыкающий к моменту t:

Рис. 9.

Назовем плотностью вероятности перехода предел отношения вероятности перехода системы за время Δt из состояния S_i в состояние S_j к длине промежутка Δt:

где – вероятность того, что система, находившаяся в момент t в состоянии S_i, за время Δt перейдет из него в состояние S_j.

При малом Δt вероятность перехода равна (с точностью до бесконечно малых высших порядков):

Если все плотности вероятностей перехода не зависят от t, марковский процесс называется однородным. Если ходя бы одна из плотностей вероятностей зависит от времени ( ), процесс называется неоднородным.

Так же, как и для марковских процессов с дискретным временем, для процесса с непрерывным временем строится размеченный граф состояний, в котором каждой дуге приписана плотность вероятности перехода.

В качестве примера рассмотрим систему S с четырьмя возможными состояниями: S₁, S₂, S₃, S₄ и размеченным графом состояний, приведенном на рис. 10.

Рис. 10.

Найдем вероятность того, что в момент времени t система будет находиться в состоянии S₁.

Придадим t малое приращение Δt и найдем вероятность события: "система в момент времени t + Δt будет находиться в состоянии S₁". Согласно размеченному графу на рис. 10, это событие может произойти двумя способами:

1. в момент t система уже была в состоянии S₁ и за время Δt не вышла из этого состояния;

или

2. в момент t система была в состоянии S₃ и за время Δt перешла из него в состояние S₁.

Вероятность первого варианта равна вероятности того, что в момент t система была в состоянии S₁ (т.е. ), умноженной на условную вероятность того, что, будучи в состоянии S₁, система за время Δt не перейдет в состояние S₂. Эта условная вероятность (с точностью до бесконечно малых высших порядков) равна .

Вероятность второго варианта равна вероятности того, что в момент t система была в состоянии S₃ (т.е. ), умноженной на условную вероятность перехода за время Δt в состояние S₁, равную

Так как эти варианты взаимоисключающие, то, по правилу сложения вероятностей, получим:

Отсюда получаем:

Устремим Δt к нулю и перейдем к пределу:

Левая часть равенства есть производная функции по времени:

Таким образом, мы получили дифференциальное уравнение, которому должна удовлетворять функция .

Рассмотрим второе состояние. Событие "система в момент времени t + Δt будет находиться в состоянии S₂" может произойти тремя способами:

1. в момент t система уже была в состоянии S₂ и за время Δt не вышла из этого состояния;

или

2. в момент t система была в состоянии S₁ и за время Δt перешла из него в состояние S₂;

или

3. в момент t система была в состоянии S₄ и за время Δt перешла из него в состояние S₂.

Вероятность первого варианта равна вероятности того, что в момент t система была в состоянии S₂ (т.е. ), умноженной на условную вероятность того, что система за время Δt не перейдет из него ни в S₃, ни в S₄. Так как события, состоящие в переходе за время Δt из S₂ в S₃ и из S₂ в S₄ несовместны, то вероятность того, что осуществится один из этих переходов, равна сумме их вероятностей, т.е. (с точностью до бесконечно малых высших порядков). А вероятность того, что не совершится ни один из этих переходов, равна . Отсюда вероятность первого варианта:

Прибавляя вероятности второго и третьего вариантов, получим:

Перенося в левую часть, деля на Δt и переходя к пределу, получим дифференциальное уравнение для :

Рассуждая аналогичным образом для состояний S₃, S₄, получим в результате систему дифференциальных уравнений (для краткости отбросим аргумент t у функций p_i):

Эти уравнения для вероятностей состояний называются уравнениями Колмогорова.

[Колмогоров Андрей Николаевич (1903 - 1987) – выдающийся советский математик, один из основоположников современной теории вероятностей, им получены фундаментальные результаты в топологии, математической логике, теории сложности алгоритмов и ряде других областей математики и её приложений.]

Решение полученной системы уравнений даст нам вероятности состояний как функции времени. В общем случае решение выполняется посредством численного интегрирования, но для однородных марковских процессов уравнения Колмогорова представляют собой систему обыкновенных дифференциальных уравнений с постоянными коэффициентами и могут быть решены аналитически.

При решении необходимо задать начальные условия в зависимости от того, каково было начальное состояние системы. Например, если в начальный момент времени (при t = 0) система находилась в состоянии S₁, то надо принять следующие начальные условия:

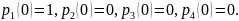
Заметим, что сумма правых частей всех уравнений системы всегда равна нулю. Это следует из того, что сумма вероятностей состояний в любой момент времени равна единице:

Дифференцируя это равенство, получим: