Однородная марковская цепь
Рассмотрим однородную марковскую цепь.
Пусть система S имеет n
возможных состояний S1,
S2, …, Sn,
и для каждого состояния
известна вероятность pij
перехода в любое другое состояние
за один шаг (в том числе и вероятность
задержки в состоянии
).
Запишем переходные вероятности в виде
квадратной матрицы переходных
вероятностей P
размерности
:
.
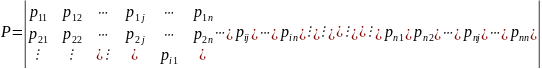Некоторые из переходных вероятностей pij могут быть равны нулю. Это означает что за один шаг переход системы из i-го состояния в j-е невозможен. По диагонали матрицы P стоят вероятности pii того, что система останется в i-м состоянии. Сумма элементов в каждой строке матрицы P равна единице, так как события несовместимы и образуют полную группу.
При рассмотрении марковских процессов удобно пользоваться размеченным графом состояний. В качестве примера проставим в графе на рис. 5 переходные вероятности, соответствующие дугам (рис. 7):
Рис. 7.
На рис. 7 проставлены не все переходные
вероятности, а только те из них, которые
не равны нулю и меняют состояние
системы (то есть pij
при
).
Вероятность pii
задержки системы в состоянии Si
равна единице минус сумма вероятностей
перехода из этого состояния в другие
состояния:
Например, для графа на рис. 7:
Имея матрицу переходных вероятностей или размеченный граф состояний и зная начальное состояние системы, можно найти вектор вероятностей состояний v(k) после любого (k-го) шага.
Пусть в начальный момент перед первым
шагом система находится в каком-либо
состоянии, например,
.
Тогда для начального момента (0) будем
иметь:
,
или в векторной форме:
,
то есть вероятности всех состояний равны нулю, кроме вероятности начального состояния , которая равна единице.
Найдем вероятности состояний после первого шага. Так как перед первым шагом система находится во состоянии , то после первого шага она перейдет в состояния S1, S2, … , Sm, … , Sn с вероятностями, записанными в m-й строке матрицы переходных вероятностей P:
или в векторной форме:
.
Этот же результат можно получить путем умножения транспонированной матрицы переходных вероятностей на вектор вероятностей состояний в момент 0:
Найдем вероятности состояний после второго шага. Будем вычислять их по формуле полной вероятности:
Иначе говоря, вероятность того, что после второго шага система окажется в состоянии равна:
вероятности того, что после шага 1 система находилась в состоянии , умноженной на вероятность перехода из состояния в , плюс
вероятность того, что после шага 1 система находилась в состоянии , умноженная на вероятность перехода из состояния в , плюс
… , плюс
вероятность того, что после шага 1 система находилась в состоянии , умноженная на вероятность перехода из состояния в , плюс
… , плюс
вероятность того, что после шага 1 система находилась в состоянии
,
умноженная на вероятность перехода из
состояния
в
.
В матричной форме этот результат получается путем умножения транспонированной матрицы переходных вероятностей на вектор вероятностей состояний в момент 1:
Аналогичным образом вычисляются вероятности состояний после третьего шага:
или в матричной форме
И вообще после k-го шага:
или в матричной форме
В силу ассоциативности операции умножения матриц последнюю формулу можно записать без рекурсии:
Итак, зная матрицу переходных вероятностей и начальное состояние системы можно вычислить вероятности состояний системы после любого шага.
Пример. По некоторой цели ведется стрельба 4 выстрелами в моменты времени t1, t2, t3, t4. Возможные состояния цели:
S1 – цель невредима;
S2 – цель незначительно повреждена;
S3 – цель получила существенные повреждения;
S4 – цель полностью повреждена и не может функционировать.
Вероятности перехода цели из состояния в состояния после каждого выстрела известны. Запишем их в виде размеченного графа:
Рис. 8.
В начальный момент времени цель находится в состоянии S1 (цель невредима). Необходимо определить вероятности состояний цели после 4 выстрелов.
Запишем переходные вероятности:
; 
; 
; 
;
; 
; 
; 
;
; 
; 
; 
;
; 
; 
; 
;
или в матричной форме:
Так как в начальный момент времени цель находится в состоянии S1, вектор вероятностей состояний системы в начальный момент равен
Вектор вероятностей состояний цели после первого выстрела:
После второго выстрела:
После третьего выстрела:
После четвертого выстрела:
Отметим, что сумма элементов вектора вероятностей состояний на любом шаге равна единице.
Таким образом, вероятности состояний цели после 4 выстрелов:
цель невредима:
;цель незначительно повреждена:
;цель получила существенные повреждения:
;цель полностью повреждена и не может функционировать:
.