
- •1 Вопрос. Основные определения: рабочая машина, узел, соединение, деталь. Требования к деталям и узлам машин.
- •2 Вопрос. Стадии конструирования машин. Требования к материалам деталей машин. Классификация, типы, и основные требования к соединениям.
- •4 Вопрос. По какому условию определяют высоту стандартной гайки.
- •10 Вопрос. Определение расчетной нагрузки наиболее нагруженного болта в соединении с группой болтов.
- •11 Вопрос. Как образуется заклепочное соединение. Коэффициент прочности φ заклепочного соединения, способы его увеличения.
- •12 Вопрос. Оценка сварного соединения по сравнению с заклепочным. Сравнить соединения встык и внахлестку, их достоинства и недостатки.
- •13 Вопрос. В чем преимущества вогнутой формы поперечного сечения углового шва. Расчёт на прочность полос, сваренных встык.
- •14 Вопрос. Почему не рекомендуется применять длинные фланговые швы.
- •16 Вопрос. Схема образования прессового соединения. Расчет прочности прессого соединения.
- •17 Вопрос. Определение расчетного натяга прессового соединения.
- •18 Вопрос. Оценка прессового соединения по сравнению со шпоночными и шлицевыми соединениями. Конические соединения. Виды шпоночных соединений. Особенности расчета стандартных шпонок.
- •19 Вопрос. Преимущества шлицевого соединения по сравнению со шпоночным соединением.
- •20 Вопрос. Конструкция зубчатых (шлицевых) соединений и критерии их работоспособности.
4 Вопрос. По какому условию определяют высоту стандартной гайки.
H = 0,8 d – условие определение высоты стандартной гайки. Н- высота гайки
Кроме нормальных, стандартом предусмотрены высокие H=1,2 d и низкие H = 0,5 d гайки. Прочность резьбы при нормальных и высоких гайках превышает прочность стержня винта. Стандартные высоты гаек (за исключением низких) и глубины завинчивания исключают необходимость расчета на прочность резьбы стандартных крепежных деталей.
5,6,7,8,9 Вопросы. Типовые случаи нагрузки болта. В каких конструкциях такие случаи встречаются. Как рассчитывают болты, поставленные с зазором и без зазора в соединениях при сдвиге нагрузки. Расчет на пресность стержня винта нагруженного на болт, из условия нераскрытого стыка.

(5 вопрос рассматриваются все 4 случая)Первый случай
Примером служит резьбовой участок грузового болта для подвешивания груза. Опасным является сечение, ослабленное резьбой. Площадь этого сечения оценивают приближенно по внутреннему диаметру d1 резьбы. Условие прочности по напряжениям растяжения в стержне,где допускаемое напряжение для растягивающей внешней нагрузки без затяжки болтов [σ] = 0,6 T
σ= F/[(π/4)·d1 2]≤ [σ]

Второй случай. Примером служат болты для крепления ненагруженных герметичных крышек и люков корпусов машин. В этом случае стержень болта растягивается осевой силой Fзат, возникающей от затяжки болта, и закручивается моментом сил трения в резьбе Тр, т.е. работает на кручение. Прочность болта определяют по эквивалентному напряжению Для стандартных метрических резьб расчеты показывают, что σэкв = 1,3σ. Это позволяет производить расчет прочности болтов по упрощенной формуле. В среднем и тяжелом машиностроении не рекомендуют применять болты малых диаметров (меньше М8), т.к. их можно разрушить при недостаточно квалифицированной затяжке.
σэкв=
 ≤[σ]
≤[σ]
σэкв = 1,3·F/[(π/4)·d1 2]≤ [σ]
 зазор
зазор
 без
зазора
без
зазора
(6 вопрос)Третий случай. Условием надежности соединения является отсутствие сдвига деталей в стыке. Конструкция может быть выполнена в двух вариантах: первый, болт поставлен с зазором; второй – болт поставлен без зазора. Болт поставлен с зазором. Внешняя нагрузка уравновешивается силами трения в стыке, которые образуются от затяжки болта. Без затяжки болтов детали могут сдвигаться на величину зазора, что недопустимо. Рассматривая равновесие детали 2, получаем условие отсутствия сдвига деталей
F< i Fтр=i Fзат f, или Fзат=KF/(if),
где i – число плоскостей сдвига деталей (на рисунке i = 2); f – коэффициент трения в стыке;( f = 0,15…0,20); K – коэффициент запаса (K = 1,3…1,5 при статической нагрузке, K = 1,8…2 при переменной нагрузке). Прочность болта оценивают по эквивалентному напряжению σэкв.
Болт поставлен без зазора. В этом случае отверстие под болт калибруют разверткой, а диаметр стержня болта выполняют с допуском, обеспечивающим беззазорную посадку. При расчете прочности соединения не учитывают силы трения в стыке, так как затяжка болта не обязательна. В общем случае болт можно заменить штифтом. Стержень болта рассчитывают по напряжениям среза и смятия. Условие прочности по напряжениям среза
τ= F/[(π/4)·d1 2i]≤ [τ]
Расчет на смятие производится по условным напряжениям из-за сложности установить точный закон распределения напряжений по цилиндрической поверхности деталей. При этом для средней детали (и при соединении только двух деталей).
 σсм
= F/[d·
σсм
= F/[d· ]≤
[σсм],для
крайних положения σсм
= F/2·[d·
]≤
[σсм],для
крайних положения σсм
= F/2·[d·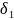 ]≤
[σсм].Из
двух значений
σсм
расчет прочности выполняют по
наибольшему, а допускаемое напряжение
определяют по более слабому материалу
болта или детали.
]≤
[σсм].Из
двух значений
σсм
расчет прочности выполняют по
наибольшему, а допускаемое напряжение
определяют по более слабому материалу
болта или детали.
(7 вопрос).Четвертый случай. Болт затянут, внешняя нагрузка раскрывает стык деталей. Примером служат болты для крепления крышек цилиндров (резервуаров), нагруженных давлением р жидкости или газа. Затяжка болтов должна обеспечить герметичность соединения или нераскрытые стыка под нагрузкой. Fзат – сила затяжки болта; F1 = F/z – внешняя нагрузка соединения (от давлении), приходящаяся на один болт; z – число болтов. Приложение внешней нагрузки вызывает дополнительную нагрузку на болт FF ,где χ– коэффициент внешней нагрузки.
а) Прочность болта при статической нагрузке:
σ = 1,3·Fр/[(π/4)·d1 2]≤ [σ]
б) Прочность болта при переменных нагрузках. При переменных нагрузках полное напряжение в болте можно разделить на постоянное (σm) и переменное с амплитудой (σа):
σм= [ Fзат +(Fб/2)]/Aб, σа= [Fб/2]/Aб,
Запас прочности по переменным напряжениям подсчитывают по формуле:
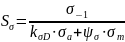
где σ-1– предел выносливости материала болта; Kσ – эффективный коэффициент концентрации напряжений в резьбе. ψσ =0,1– коэффициент чувствительности к асимметрии цикла напряжений.
(9вопрос)
χ– коэффициент внешней нагрузки.χ= λд/ (λд +λδ)
где λδ – податливость болта, равная его удлинению при единичной нагрузке; λд – суммарная податливость соединяемых деталей. Для большинства практических случаев расчет податливостей деталей связан с большими трудностями. Между тем расчеты и испытания конструкций показывают, что χ можно принять равным или меньше (0,2….0,3) для соединений без мягких прокладок. Переменные напряжения вызывают явление усталости. Чем меньше χ , тем выше сопротивление болта усталости. При этом, упругие болты – хорошая защита от усталостного разрушения.
