13. Параллельность прямых и плоскостей в пространстве

Раздел о параллельности прямой и плоскости следует начать с беседы о возможном числе общих точек у прямой и плоскости, опи­раясь при этом на соответствующую аксиому (Б10).

Прямая и плоскость не могут иметь только две общие точки, ибо в противном случае прямая будет лежать в этой плоскости. По той же причине прямая не может иметь с плоскостью только три, четы­ре и т. д. общих точек.

Может ли прямая иметь с плоскостью только одну общую точку? Как показывает опыт, да.

Надо построить прямую, имеющую с плоскостью только одну об­щую точку, и обосновать это (рис. 113):

1. На плоскости а выбрать точку О.

2. Вне плоскости а выбрать точку М.

3. Точки М и О определяют единственную прямую b.

4. b имеет с а единственную общую точку О

При доказательстве предполагаем противное, т. е. пусть b имеет с а более чем одну общую точку. Тогда b будет лежать в а. Таким образом, прямая b имеет с а только одну общую точку. В этом случае говорят, что прямая пересекает плоскость или плоскость пересекает прямую.

Остается выяснить, может ли прямая совсем не иметь с плос­костью общих точек. На основании опыта и наблюдений можно утверждать, что может.

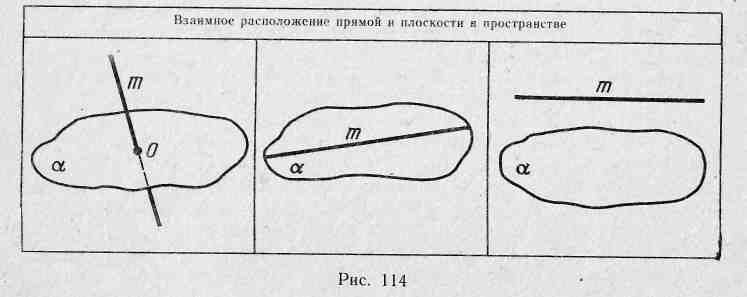
Все приведенные выше рассуждения поясняются примерами из окружающей жизни и записываются в таблицу (рис. 114):

Пользуясь таблицей, учащиеся самостоятельно могут дать опре­деление параллельности прямой и плоскости. С помощью определения не всегда можно судить о том, что данные прямая и плоскость па­раллельны, поскольку прямая и плоскость безграничны.

По опр-ию определить параллельность практически невозможно, поэтому необходим признак.

Появляется теорема, носящая имя признака параллельности прямой и плоскости, показывающая существование параллельных прямой и плоскости в пространстве.(Опред: прямая и плоскость наз –ся //, если они не пересекаются. Признак:если прямая || какой-л. прямой,принадл-ей пл-ти, то она ||пл-ти. Т.обр.к призн-у: если плос-ть проходит ч\з прямую,||ую другой пл-ти и пересекает ее, то линия пересечения ||на данной прямой).

При доказательстве теоремы используется таблица. Доказательство ведется методом от противного. Из предположения, что прямая имеет с плоскостью общую точку, приходят к противоречию с уже известной истиной. На основании этого утверждают, что прямая не может пересекаться с плоскостью, т. е. она параллельна ей.

Обрабатывается усвоение признаков на задачах: Задача : через данную точку провести прямую // ую данной плоскости

Очень важна теорема, обратная к признаку. Т: Если плоскость проходит через прямую //ую другой плоскости и пересекает ее, то линия пересечения //а данной прямой

Как правило эта теорема не акцентируется в школе.