7 . Метрические соотношения в треугольнике.

Т косинусов: Для плоского треугольника со сторонами a,b,c и углом α, противолежащим стороне a, справедливо соотношение:

Т синусов: Для произвольного треугольника,где a, b, c — стороны треугольника, α,β,γ — соответственно противолежащие им углы, а R — радиус окружности, описанной вокруг треугольника :

Неравенство треугольника: длина любой стороны треугольника всегда не превосходит сумму длин двух его других сторон. Неравенство треугольника включается как аксиома в определение метрического пространства

Выражение биссектрисы через стороны треугольника:

Из теоремы косинусов находим все углы треугольника: У1=arccos( (a^2+b^2-c^2)/2ab) и т.д.

Далее, биссектриса делит треугольник на 2 других треугольника. Биссектриса, как известно, делит угол пополам. Соответственно, достаточно рассмотреть один из двух получившихся треугольников. В нём нам известно 2 угла (а значит все углы), и прилежащая к ним сторона. Далее, пользуясь теоремой синусов, находим биссектрису.

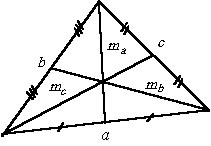
Выражение медианы через стороны треугольника:

Для нахождения медианы треугольника по трем его сторонам удобно использовать

Высота треугольника опущенная на сторону a обозначается буквой ha и через три стороны треугольника выражается формулой:

H_a= где p=1/2(a+b+c)

Нахождение радиусов:

Радиус вписанной окружности в ∆:

r= где p=1/2(a+b+c)

Радиус описанной окружности:

9. Площади плоских фигур в курсе планиметри.

Историческая справка. Это одна из главных практических задач в нахождении площади, которая послужила толчком в развитии геометрии (о том, как древние греки находили плошади). С древности люди умели находить площади различных фигур, в частности площадь круга. Длина отрезка в школе определяется следующим образом: Погорелов: Аксиома: каждый отрезок имеет определенную длину больше нуля. Длина отрезка равна сумме длин частей, на которые он разбивается на части. Аналогично у Атанасяна.

Пропедевтика. Учащиеся с понятием «площадь» знакомятся в 6 классе, вычисляют площади фигур (см. учебники 6 класса).

Систематическое изучение : 7-9 класс. Существуют два подхода: 1. Аксиоматический подход (сначала дается определение потом переходят к формулам различных фигур). через числовую функцию S, определяют на множестве плоских фигур. S называют площадью, если выполнены следующие аксиомы: а) Любая фигура равна самой себе; б) если фигура Ф равна фигуре Ф₁, то фигура Ф₁ равна фигуре Ф; в) если фигура Ф₁ равна фигуре Ф₂, а фигура Ф₂ равна фигуре Ф₃ , то фигура Ф₁ равна фигуре Ф₃. 2. Конструктивный ( сначала рассматрив-ся на различных фигурах, потом дается определение). В ВУЗе определяются фигуры, измеримые по Жордану – это класс квадрируемых фигур, т.е. тех, для которых удается доказать существование и единственность площади. Для этого вводится сеть квадратов, покрывающих фигуру. Площадь – это предел.

Этот подход характерен в основном для всех авторов. Темы излагаются в следующей последовательности: понятие площади; свойства (это и есть аксиомы); площадь с разной степенью строгости ( проблема: если измеряется иррациональное число, а теория пределов в институте); площадь треугольника; площадь четырехугольников; отношение площадей подобных фигур; площадь круга и частей.

У Погорелова аксиоматический подход(см учебник, выписать опред-е площади и опред-е площади фигур, площадь прямоугольника самая трудная) .

Атанасян начинает с площади многоугольника. Поэтому упрощается вывод площади прямоугольника. Свойства площади не доказываются. Поэтому для Атанасяна характерен не аксиоматический метод, а конструктивный, который характеризуется заданием способа вычисления, а затем обоснованием, что указанная площадь обладает выше перечисленными свойствами (аксиомами)( см учебник, списать св-ва и опред-я).

Авторы учебников Александров, Вернер, рыжик; и Шарыгин придерживаются аксиоматического метода.

Тема площади изучается у различных авторов по разному. Например, у Погорелова в 9 классе последняя тема ( у остальных смотри программу). При этом термины площадь треугольника, площадь четырехугольников позволят решать задачи не только на непосредственное нахождение площади, но и на нахождение вписанных и описанных радиусов, а также доказательству теорем планиметрии. Например, свойства биссектрис угла, выражение длин медианы, биссектрисы через стороны и другие.

Поэтому данную тему полезно рассматривать на факультативе не только в 9 классе, но и в 10, 11 классе, т.к. решение задач позволяет повторить весь курс планиметрии. В процессе изучения данной темы полезны задачи следующих типов: а) задачи на разрезание, т.е. задачи на отработку «равносоставленных, равновеликих», б) пять формул площади треугольника, т.е. на нахождение радиусов вписанных и описанных окружностей; в) задачи – софизмы.

Задача для урока по софизмам: Софизм- умозакл-е или рассуж-е обосновывающие какую ниб заведомую нелепость , апсурд или порадоксальное утверждение, противореч-ее общепринятым представ-ям 1. Вырезать из картона следующие фигуры:

С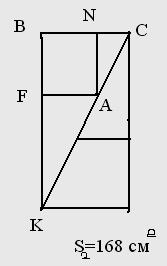 ложим из этих частей новые фигуры:

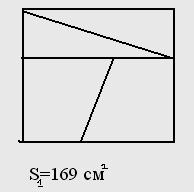
S₁≠S₂ ? / Первая фигура – квадрат, со стороной 13 см, S₁= 169 см². Во второй фигуре из точки А опустим перпендикуляр на ВС.

| точки C,A,K не лежат на одной прямой=>вторая фигура не прямоугольник, значит ее площадь нельзя вычислить по формуле

Выписать по Атанасяну и Погорелову:площадь могоуг-ка, квадрата,прямоуг-ка,параллелограмма, треуг-ка, круга, трапеции, сектора.