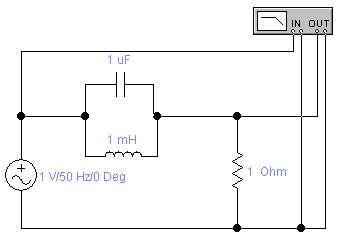
2. Вынужденные колебания в параллельном колебательном контуре. Резонанс токов

Сначала рассмотрим вынужденные колебания в параллельном колебательном контуре без потерь (r=0).

Принимаем, что при изменении частоты источника э.д.с. его амплитуда не изменяется, внутренним сопротивлением источника пренебрегаем, т.е. будем считать, что амплитуда приложенного к контуру напряжения U не изменяется.

П ри увеличении частоты сопротивление катушки индуктивности и конденсатора изменяется по уже известным законам: , . При этом изменяются токи, протекающие по катушке и через конденсатор, а также общий ток, т. е. ток в неразветвленной части цепи. Ниже, на рис.1, показаны векторные диаграммы идеального параллельного колебательного контура для различных частот источника э.д.с.

Рисунок 1

Если частота источника э.д.с. мала, то X_L< X_C, поэтому ток, протекающий через конденсатор, намного меньше, чем ток, проходящий по катушке (рис. 1, а). Общий ток ( ) будет достаточно большим, контур в целом представляет малое индуктивное сопротивление.

При увеличении частоты сопротивление катушки возрастает (рис. 1, б), а сопротивление конденсатора уменьшается; соответственно уменьшается ток , протекающий через через катушку и увеличивается ток , протекающий через конденсатор. При некоторой частоте , которую называют резонансной, сопротивление катушки и конденсатора будут равными (X_L=X_C). Следовательно, будут равны и токи: = . В этом случае общий ток =0, т.е. контур в целом представляет собой бесконечно большое сопротивление. Поскольку такое явление происходит при X_L=X_C, частота источника э.д.с. равна частоте свободных колебаний в контуре, т.е. = = .

Явление, происходящее в параллельном колебательном контуре, когда частота вынужденных колебаний совпадает с частотой свободных колебаний в нем, называется параллельным резонансом, или резонансом токов.

Физическая сущность резонанса токов состоит в том, что максимальные реактивные мощности, потребляемые катушкой и конденсатором, равны. Магнитное поле создается во время нарастания тока, когда напряжение на конденсаторе уменьшается и энергия электрического поля высвобождается. И наоборот, во время спадания тока высвобождающаяся энергия магнитного поля переходит в энергию электрического поля. Таким образом, обмен энергиями между катушкой и конденсатором происходит без участия источника э.д.с. Разумеется, что первоначальный запас энергии контур получает от источника в начальный момент включения цепи.

При дальнейшем увеличении частоты (рис. 1, в) ток в катушке индуктивности становится еще меньше, а ток, протекающий через конденсатор, – еще больше. Ток в неразветвленной части цепи носит емкостной характер и с увеличением частоты быстро возрастает.

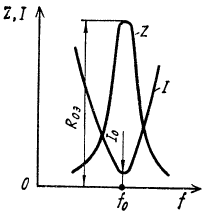
На рисунке справа показана зависимость сопротивления (Z) параллельного контура и тока в неразветвленной части цепи (питающего тока I) от частоты. Максимальное значение сопротивления и минимальное значение тока соответствуют резонансной частоте f₀.

В реальном колебательном контуре активное сопротивление катушки не равно нулю, поэтому ток в индуктивной ветви отстает от напряжения на угол φ, меньший 90^о. Резонанс токов в реальном контуре возникает тогда, когда реактивная составляющая тока в катушке становится равной току в конденсаторе .

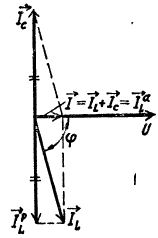Векторная диаграмма реального колебательного контура при резонансе токов представлена на рисунке справа. В этом случае ток в неразветвленной части цепи хотя и не равен нулю, но очень мал и совпадает по фазе с приложенным напряжением. Из векторной диаграммы видно, что он равен активной составляющей тока в катушке. Физически это означает, что от источника потребляется небольшое количество энергии для покрытия активных потерь в контуре, причем это количество тем меньше, чем меньше активное сопротивление контура.

Условие резонанса X_L=X_C для реального контура является приближенным, им можно пользоваться тогда, когда r << X_L.

Итак, для параллельного резонанса характерны следующие особенности:

1) Полное сопротивление контура максимально и по характеру чисто активно.

2) Токи в катушке и конденсаторе равны (точнее, ток в конденсаторе равен реактивной составляющей тока в катушке).

3) Ток в питающей цепи минимален и по фазе совпадает с напряжением.

Параллельные колебательные контуры широко применяются в РЭА и, в частности, в резонансных усилителях. Свойство контуров выделять сигналы, частоты которых равны или мало отличаются от резонансной, дает возможность избирательно усиливать сигналы.