Ход выполнения работы

1. Исследование вынужденных колебаний в последовательном

к олебательном контуре. Резонанс напряжений

Последовательный колебательный контур представляет собой цепь переменного тока с последовательно соединенными активным, индуктивным и емкостным сопротивлениями.

Общее сопротивление такой цепи

Проследим за изменением значения и характера общего сопротивления последовательного контура при изменении частоты источника переменной э.д.с. При этом будем считать, что внутреннее сопротивление источника э.д.с. равно нулю, т.е. амплитуда напряжения U на зажимах контура не изменяется.

А ктивное сопротивление контура (в первом приближении) от частоты не зависит и при изменении частоты не изменяется.

При постепенном увеличении частоты f от нуля (нулевая частота соответствует постоянному току) индуктивное сопротивление катушки возрастает по закону прямой пропорциональности, а емкостное сопротивление конденсатора уменьшается по закону обратной пропорциональности (X_L на рис.1 отложена как положительная величина, а X_С – как отрицательная).

Общее реактивное сопротивление контура

Х = X_L – X_С

при малой частоте велико и по характеру – емкостное. По мере увеличения частоты оно постепенно уменьшается и при некоторой частоте f _РЕЗ , которую называют резонансной, становится равным нулю. В этом случае X_L = X_С , а резонансная частота равна частоте собственных колебаний в контуре f _о .

, откуда .

Полученный результат можно сформулировать и так: при резонансе общее сопротивление последовательного контура равно нулю.

При дальнейшем увеличении частоты общее реактивное сопротивление возрастает и носит индуктивный характер.

Полное сопротивление контура при увеличении частоты сначала уменьшается, достигая значения r при резонансе (т.е. при f=f _о), а затем вновь возрастает. На частотах f <f _о полное сопротивление контура имеет активно-емкостной характер, а на частотах f >f _о – активно-индуктивный. На частоте резонанса (f=f _о) полное сопротивление по характеру чисто активное и равно активному сопротивлению контура.

Таким образом, в последовательном колебательном контуре при изменении частоты источника э.д.с. происходят резкие изменения характера и значения полного сопротивления.

Явления, происходящие в последовательном контуре, когда частота вынужденных колебаний совпадает с частотой его свободных колебаний, называются последовательным резонансом, или резонансом напряжений.

Для последовательного резонанса характерны следующие особенности:

1) Полное сопротивление контура минимально, по характеру чисто активно и равно активному сопротивлению контура r.

2) Поскольку сопротивление контура минимально и по характеру чисто активно, ток в последовательном контуре при резонансе максимален и по фазе совпадает с приложенным напряжением.

3) Напряжения на конденсаторе и катушке индуктивности равны по значению и в Q раз превышают приложенное напряжение.

Действительно, по закону Ома напряжение, приложенное к зажимам контура, ; в то же время напряжение на конденсаторе . Взяв отношение , получим . Так как X_L = X_С , очевидно, что и .

Р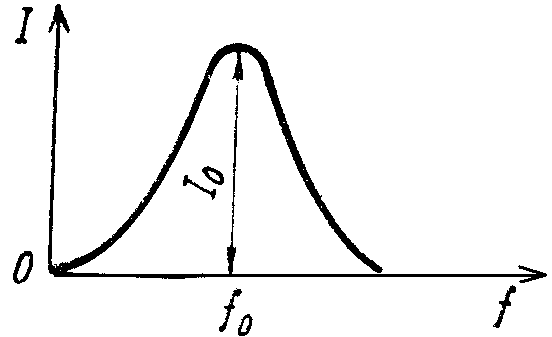 езкое увеличение напряжений на катушке и конденсаторе при последовательном резонансе и послужило основанием для того, чтобы назвать резонанс в последовательном контуре резонансом напряжений.

Ф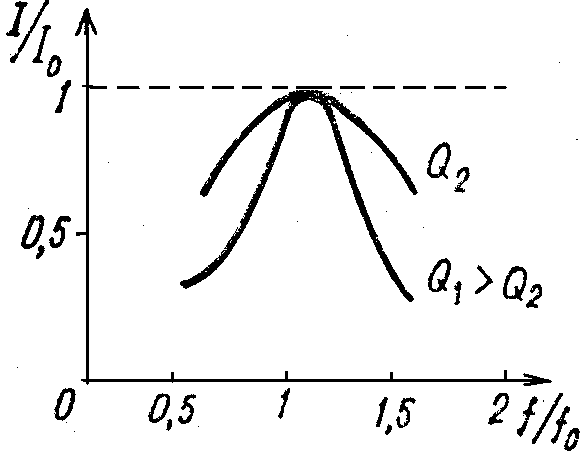 орма графика зависимости тока в последовательном контуре от частоты зависит от добротности контура Q. Если уменьшить активное сопротивление контура, то значение тока при резонансе будет возрастать, т.е. вершина кривой будет становиться уже, а скаты её – круче. Таким образом, при прочих равных условиях, чем выше добротность, тем острее резонансная кривая.

Резонансные кривые удобно строить в относительном масштабе, откладывая по оси ординат отношение , а по оси абсцисс – . В этом масштабе отчетливо видна зависимость формы резонансной кривой от добротности контура.

Очевидно, что если на последовательный колебательный контур воздействуют одинаковые по амплитуде, но разные по частоте э.д.с., то создаваемые ими токи будут тем больше, чем ближе частота соответствующей э.д.с. к частоте свободных колебаний в контуре. Таким образом, контур обладает избирательностью, т.е. способностью усиливать сигналы одних частот относительно других.

И збирательные свойства колебательного контура оценивают по полосе пропускания.

Полосой пропускания называется полоса частот, в пределах которой значение тока (напряжения) уменьшается не более чем в =1,41 раза по сравнению с резонансным. При этом мощность уменьшается в два раза.

Такое определение исходит из того факта, что при уменьшении мощности сигнала в два раза ослабление громкости на слух практически не ощущается.

Полоса пропускания может быть определена по формуле

.

Н а рис. показан пример использования резонанса напряжений. Э.д.с., наводимая в антенном контуре приемника током, протекающем по антенне, включена последовательно относительно его индуктивности и емкости. Измененим емкости конденсатора контур настраивается на частоту сигнала, при этом ток в нем достигает максимума, а напряжение, снимаемое с конденсатора, в Q раз превышает наводимую э.д.с. Сигналы же других частот (помех) при том же значении э.д.с. создают в антенном контуре малый ток и малое напряжение на конденсаторе.