3. Параметризация модели
-
Статистической оценкой параметра называется его приближенное значение, полученное на основе выборочных данных. Для получения точечных оценок параметров уравнения парной линейной регрессии применяют метод наименьших квадратов (МНК). В соответствии с МНК минимизируется сумма квадратов разностей между фактическими и расчетными значениями зависимой переменной. Оценки неизвестных параметров находятся из системы нормальных уравнений, полученной методом дифференциального исчисления.
Для расчета интервальных оценок (доверительных интервалов) параметров регрессии определяются предельные ошибки для каждого показателя:
где
– стандартные ошибки коэф-
фициентов
регрессии;
– стандартная ошибка регрессии,
которая служит мерой разброса зависимой
переменной вокруг линии регрессии;
– критическая точка распределения
Стьюдента для заданного уровня
значимости и
числа степеней свободы
v = n – 2.
Доверительные
интервалы имеют вид: для b0 –
(
),
–
(
),
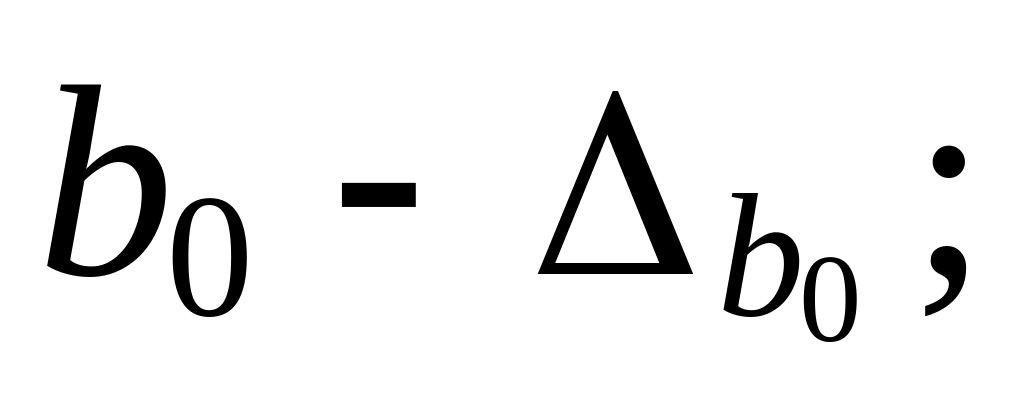
где центр интервала равен точечной
оценке, концы интервалов получены
прибавлением и
вычитанием произведения стандартной
ошибки коэффициента на критическое
значение t-статистики.Доверительный интервал с вероятностью 0,95 содержит истинное значение свободного члена уравнения регрессии. Поэтому любое значение из этого интервала может служить оценкой параметра. Если в границы доверительного интервала попадает ноль, т. е. нижняя граница отрицательна, а верхняя – положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
В результате проведения регрессионного анализа на листе «Регрессия» в третьей таблице получены точечные и интервальные оценки неизвестных параметров (таблица 6).
Таблица 6 – Статистика коэффициентов регрессии
|
Коэффи- циенты |
Стандарт- ная ошибка |
t-статис- тика |
P-Значение |
Нижние 95% |
Верхние 95% |
Y-пересе- чение |
–73,25 |
16,03 |
–4,57 |
0,000 24 |
–106,93 |
–39,56 |
ВВП |
0,26 |
0,01 |
25,93 |
0,000 00 |
0,24 |
0,28 |
|
|
tкр |
2,10 |
|
|
|
Точечная оценка параметра b0 равна –73,25. Интервальная оценка равна (–106,93; –39,56). Доверительный интервал с вероятностью 0,95 содержит истинное значение свободного члена уравнения регрессии. Поэтому любое значение из этого интервала может служить оценкой параметра b0.
Точечная оценка параметра b1 равна 0,24. Интервальная оценка равна (0,24; 0,28). Доверительный интервал с вероятностью 0,95 содержит истинное значение коэффициента при переменной x уравнения регрессии. Поэтому любое значение из этого интервала может служить оценкой параметра b1.
Таким образом, уравнение регрессии имеет вид
y = –73,25 + 0,24x.
Случайная переменная отсутствует в уравнении, так как коэффициенты регрессии имеют случайный характер, т. е. неучтенные факторы повлияли на их значение при применении МНК.