- •Статистические и геометрические вероятности. Задача о встрече.
- •Перестановки. Число перестановок во множестве из n-элементов. Сочетания. Число сочетаний по k-элементам во множестве из n-элементов. Размещение. Примеры применения в подсчете их вероятностей.
- •Сумма событий. Теорема о сложении вероятностей несовместных событий. Произведение событий, условные вероятности. Теорема умножения вероятностей.
- •Полная группа событий. Противоположные события. Вероятность появления хотя бы одного события. Формула полной вероятности.
- •Формулы Бейеса. Вероятность суммы двух совместных событий.
- •Повторение испытаний. Формула Бернулли. Локальная теорема Муавра-Лапласа.
- •Повторение испытаний. Интегральная теорема Лапласа. Формула Пуассона.
- •Случайные величины. Дискретные и непрерывные случайные величины. Закон распределения. Дискретные случайные величины. Математическое ожидание дискретной случайной величины.
- •Вероятностный смысл математического ожидания дискретной случайной величины, его свойство.
- •Дисперсия дискретной случайной величины, свойство 3 дисперсии дискретной случайной величины.
- •Дисперсия дискретной случайной величины. Свойство 1-2 дисперсии. Среднеквадратическое отклонение. Геометрическое распределение. Гипергеометрическое распределение.
- •Вероятность попадания непрерывной случайной величины в заданный интервал. Плотность вероятности . Ее свойства.
- •Системы случайных величин (случайные векторы, двумерные случайные величины). Закон распределения дискретной двумерной случайной величины. Законы распределения ее составляющих х и у.
- •28.Вероятность попадания непрерывной двумерной случайной величины в полуполосу и прямоугольник.
- •30.Вероятность попадания двумерной случайной величины в произвольную область. Свойства нормировки для .
- •31.Отыскание составляющих двумерной случайной величины х и у , а также .
- •32.Необходимые и достаточные условия независимости случайных величин х и у.
- •33.Корреляционный момент случайных величин х и у. Формулы для его нахождения для дискретной случайной величины и непрерывной случайной величины.
- •34.Коэффициент корреляции, его свойства.
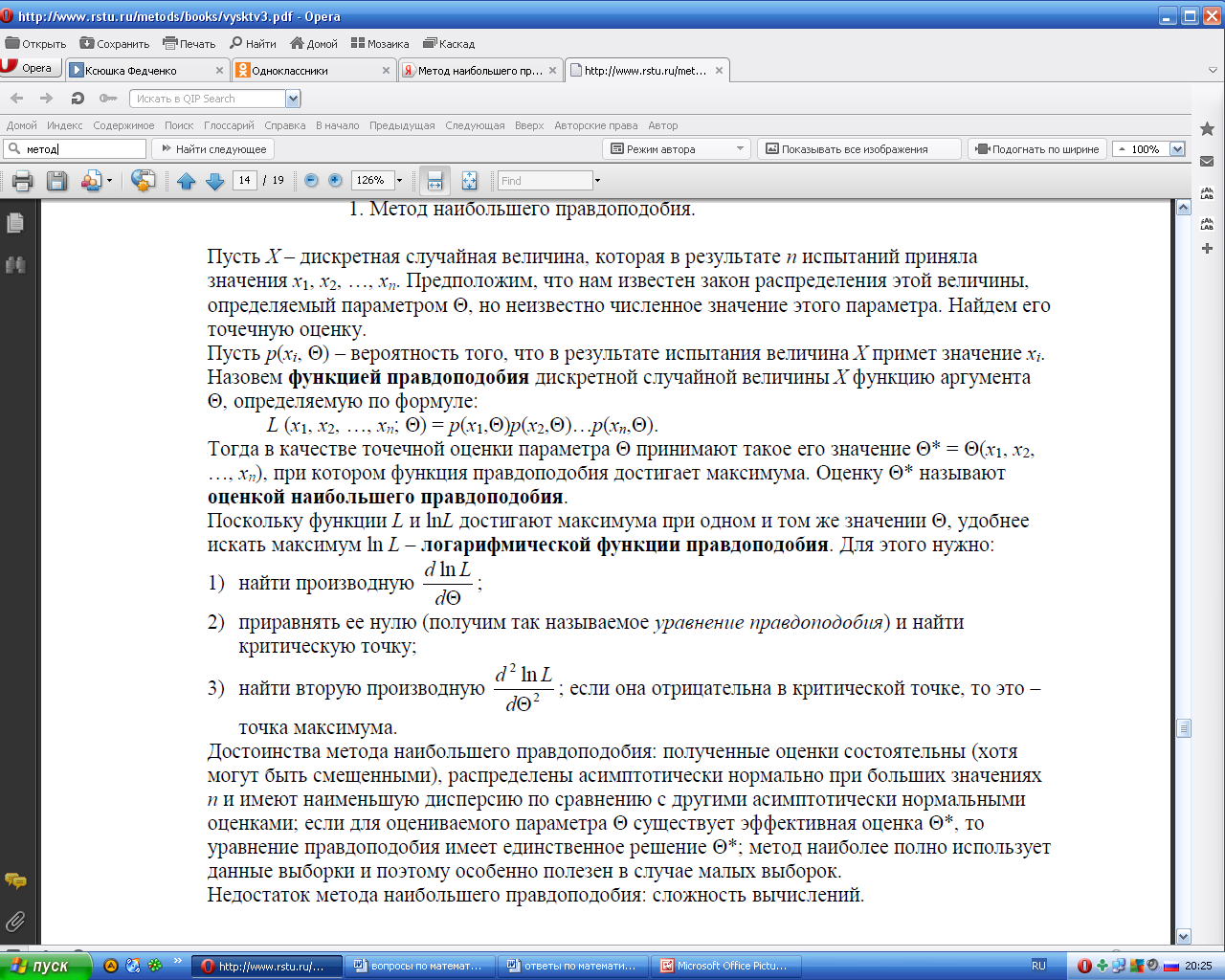
- •39.Метод наибольшего правдоподобия для определенных параметров непрерывной случайной величины. Метод моментов для их определения. Метод моментов для двух параметрических величин
34.Коэффициент корреляции, его свойства.
Коэффициентом
корреляции
![]() случайных величин Х и Y называется
отношение корреляционного момента к
произведению среднеквадратических
отклонений этих величин.
случайных величин Х и Y называется
отношение корреляционного момента к
произведению среднеквадратических
отклонений этих величин.
![]()
Коэффициент корреляции является безразмерной величиной. Коэффициент корреляции независимых случайных величин равен нулю.
Свойство 1: Абсолютная величина корреляционного момента двух случайных величин Х и Yне превышает среднего геометрического их дисперсий.
Свойство
2: Абсолютная величина коэффициента
корреляции не превышает единицы.
![]() Случайные величины называются
коррелированными, если их корреляционный
момент отличен от нуля, и некоррелированными,
если их корреляционный момент равен
нулю. Если случайные величины независимы,
то они и некоррелированы, но из
некоррелированности нельзя сделать
вывод о их независимости. Если две
величины зависимы, то они могут быть
как коррелированными, так и
некоррелированными. Часто по заданной
плотности распределения системы
случайных величин можно определить
зависимость или независимость этих
величин.
Случайные величины называются
коррелированными, если их корреляционный
момент отличен от нуля, и некоррелированными,
если их корреляционный момент равен
нулю. Если случайные величины независимы,
то они и некоррелированы, но из
некоррелированности нельзя сделать
вывод о их независимости. Если две
величины зависимы, то они могут быть
как коррелированными, так и
некоррелированными. Часто по заданной
плотности распределения системы
случайных величин можно определить
зависимость или независимость этих
величин.
37. Генеральная и выборочная совокупности, повторные, бесповторные выборки, способы отбора. Обеспечение случайности и репрезентативности выборки. Вариационный ряд и его характеристики. Полигон частот и полигон относительных частот. Гистограммы.
Различают генеральную и выборочную совокупности:
Генеральной совокупностью называют совокупность всех мысленно возможных объектов данного вида, над которыми проводятся наблюдения с целью получения конкретных значений случайной величины, или совокупность результатов всех мыслимых наблюдений, проводимых в неизменных условиях над одной из случайных величин, связанных с данным видом объектов.
Замечание: Часто генеральная совокупность содержит конечное число объектов. Однако если это число достаточно велико, то иногда в целях упрощения вычислений допускают, что генеральная совокупность состоит из бесчисленного множества объектов. Такое допущение оправдывается тем, что увеличение объема генеральной совокупности (достаточно большого объема) практически не сказывается на результатах обработки данных выборки.
Выборочной совокупностью называют часть отобранных объектов из генеральной совокупности. Число объектов генеральной совокупности N значительно превосходит объем выборки n .
При составлении выборки можно поступать двумя способами: после того как объект отобран и над ним произведено наблюдение, он может быть возвращен либо не возвращен в генеральную совокупность. В соответствии со сказанным выборки подразделяют на повторные и бесповторные.
Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.
Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.
На практике обычно пользуются бесповторным случайным отбором.
На практике применяются различные способы отбора. Принципиально эти способы можно подразделить на два вида:
1. Отбор, не требующий расчленения генеральной совокупности на части. Сюда относятся: а) простой случайный бесповторный отбор; б) простой случайный повторный отбор.
2. Отбор, при котором генеральная совокупность разбивается на части. Сюда относятся: а) типический отбор;б) механический отбор; в) серийный отбор.
Простым случайным называют такой отбор, при котором объекты извлекают по одному из всей генеральной совокупности и после обследования не возвращают (бесповторный отбор) или возвращают ( повторный отбор) в генеральную совокупность.
Типическим называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее «типической» части
Механическим называют отбор, при котором генеральную совокупность «механически» делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект.
Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергаются сплошному обследованию.
Вариационным рядом называется последовательность всех элементов выборки, расположенных в неубывающем порядке. Одинаковые элементы повторяются.
Вариационный ряд характеризуется следующими параметрами:
Мода- варианта, имеющая наибольшую частоту
Медиана- варианта, которая делит этот ряд на две равные части
Размах вариации
-
![]() .
.
Полигоном частот называют ломаную линию, отрезки, которой соединяют точки (x1;n1), (x2;n2), …, (xk;nk). Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат – соответствующие им частоты ni.
Полигоном относительных частот называют ломаную линию, отрезки которой соединяют точки (x1; p1*), (x2; p2*), … , (xk; pk*). Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат – соответствующие им относительные частоты pi*.
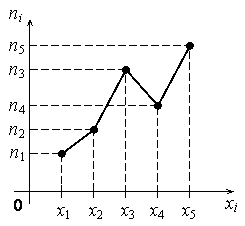
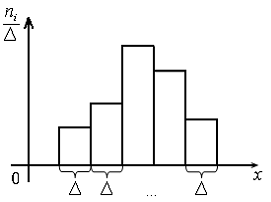
Гистограммой частот называется ступенчатая фигура, основанием i-го прямоугольника которой являются частичные интервалы длиною Δi, и высотой ni /Δi. Площадь одного прямоугольника равна ni.
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии ni /Δi.
В практике для удобства вычислений обычно используют ряды с равными интервалами (Δ).
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною Δi, а высоты равны отношению pi* / Δ i.
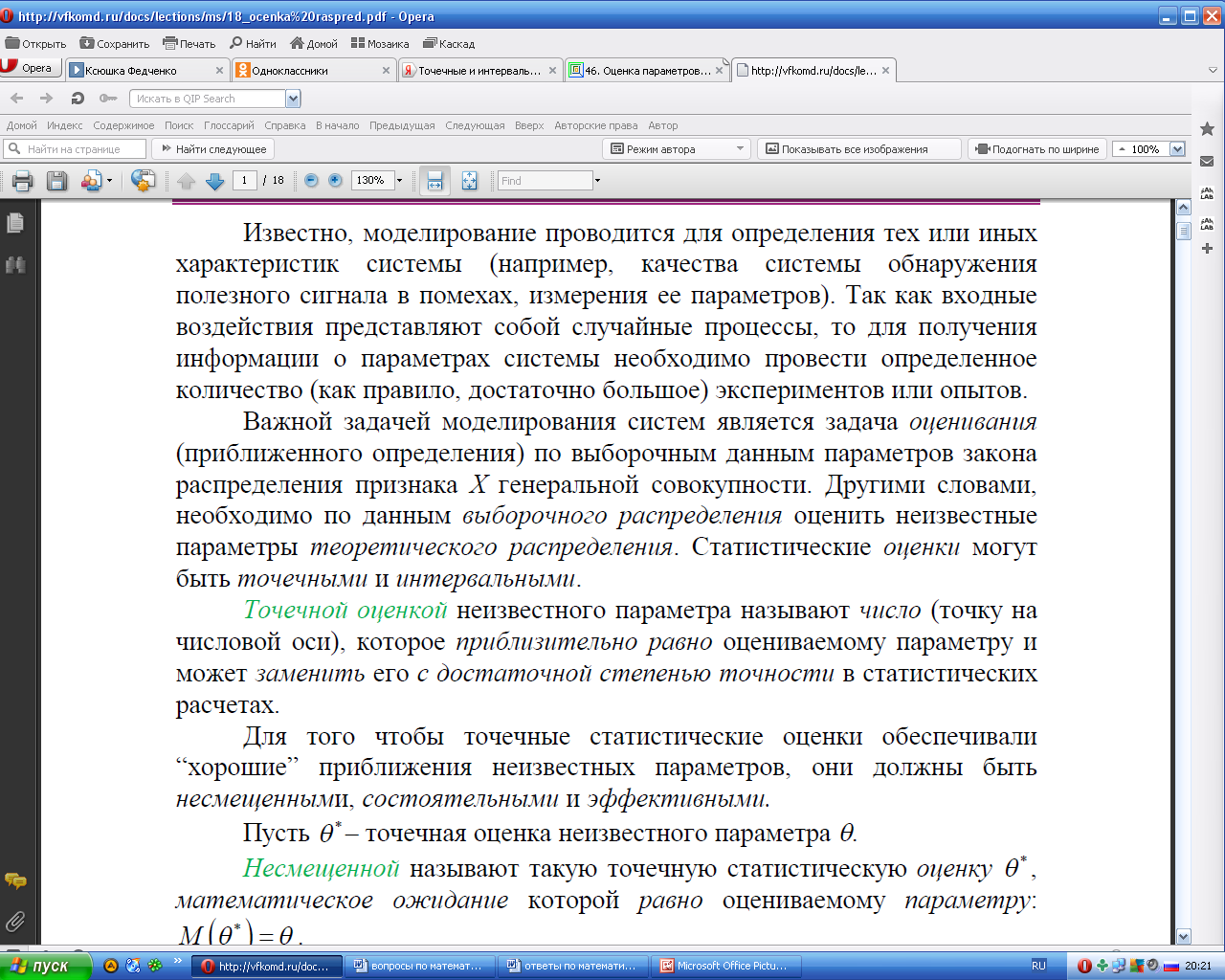
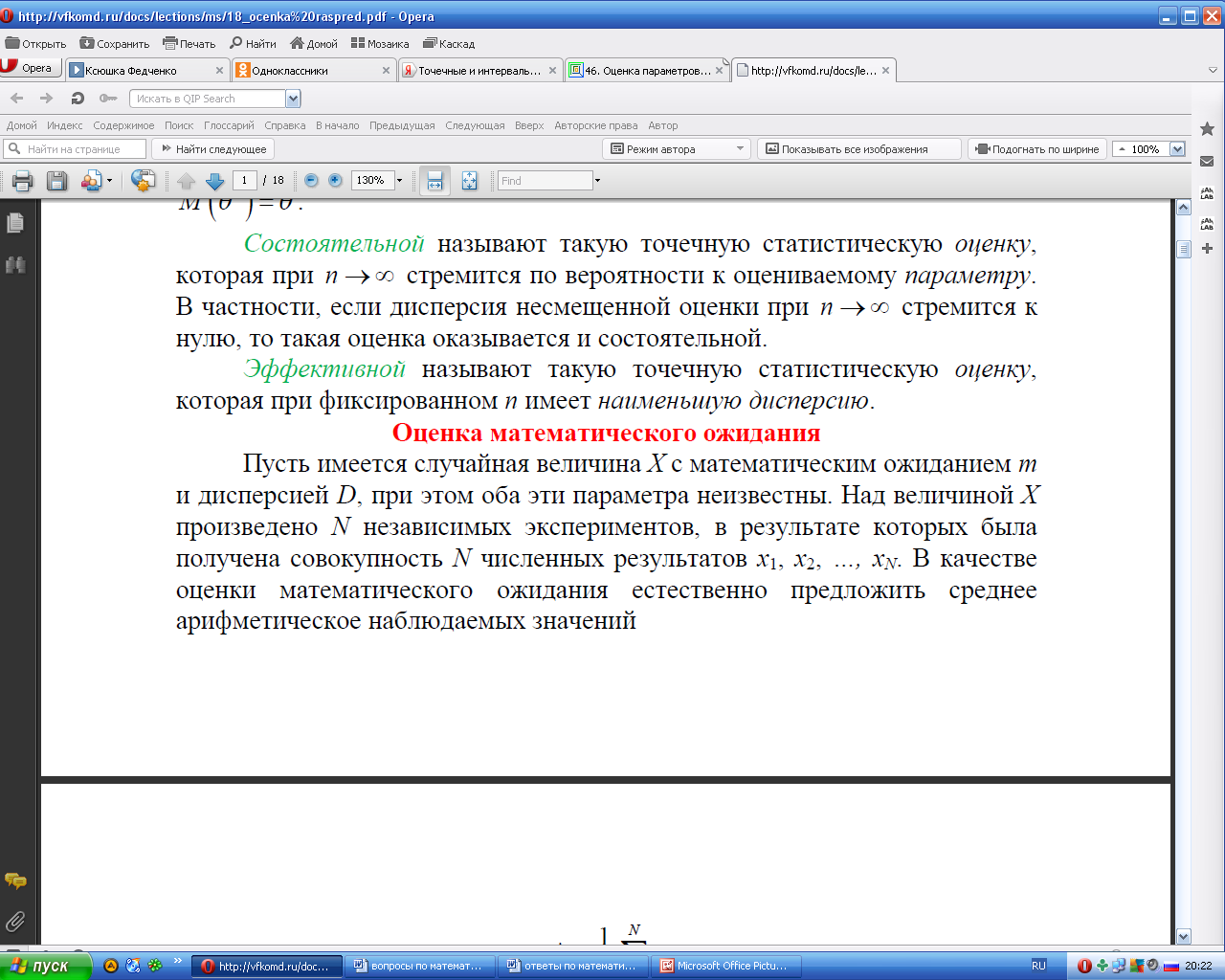
38.Точечные и интервальные оценки параметров распределения (несмещенности, эффективности, состоятельности точечных оценок). Точность и надёжность интервальной оценки. Метод наибольшего правдоподобия для дискретной случайной величины.