
- •Статистические и геометрические вероятности. Задача о встрече.
- •Перестановки. Число перестановок во множестве из n-элементов. Сочетания. Число сочетаний по k-элементам во множестве из n-элементов. Размещение. Примеры применения в подсчете их вероятностей.
- •Сумма событий. Теорема о сложении вероятностей несовместных событий. Произведение событий, условные вероятности. Теорема умножения вероятностей.
- •Полная группа событий. Противоположные события. Вероятность появления хотя бы одного события. Формула полной вероятности.
- •Формулы Бейеса. Вероятность суммы двух совместных событий.
- •Повторение испытаний. Формула Бернулли. Локальная теорема Муавра-Лапласа.
- •Повторение испытаний. Интегральная теорема Лапласа. Формула Пуассона.
- •Случайные величины. Дискретные и непрерывные случайные величины. Закон распределения. Дискретные случайные величины. Математическое ожидание дискретной случайной величины.
- •Вероятностный смысл математического ожидания дискретной случайной величины, его свойство.
- •Дисперсия дискретной случайной величины, свойство 3 дисперсии дискретной случайной величины.
- •Дисперсия дискретной случайной величины. Свойство 1-2 дисперсии. Среднеквадратическое отклонение. Геометрическое распределение. Гипергеометрическое распределение.
- •Вероятность попадания непрерывной случайной величины в заданный интервал. Плотность вероятности . Ее свойства.
- •Системы случайных величин (случайные векторы, двумерные случайные величины). Закон распределения дискретной двумерной случайной величины. Законы распределения ее составляющих х и у.
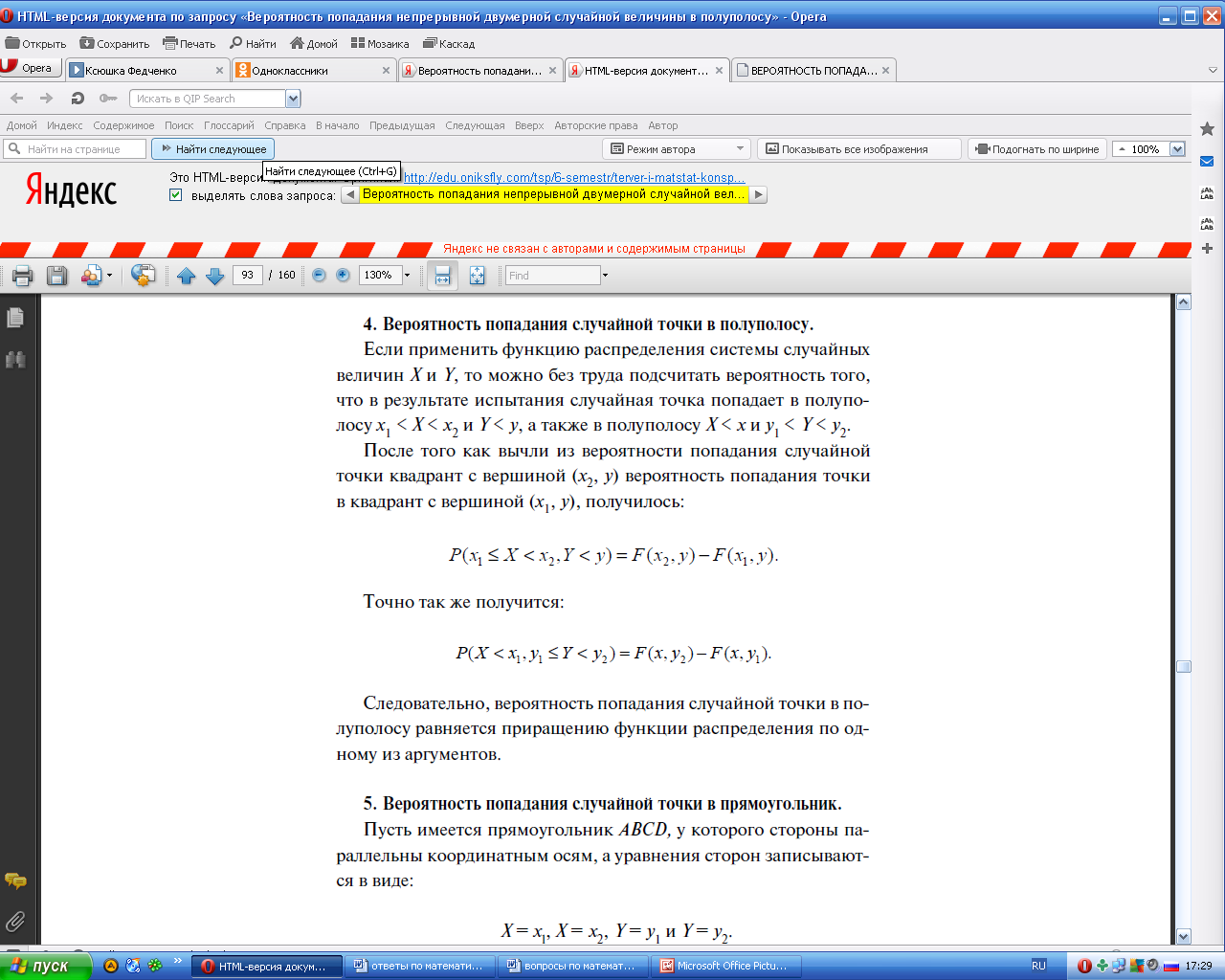
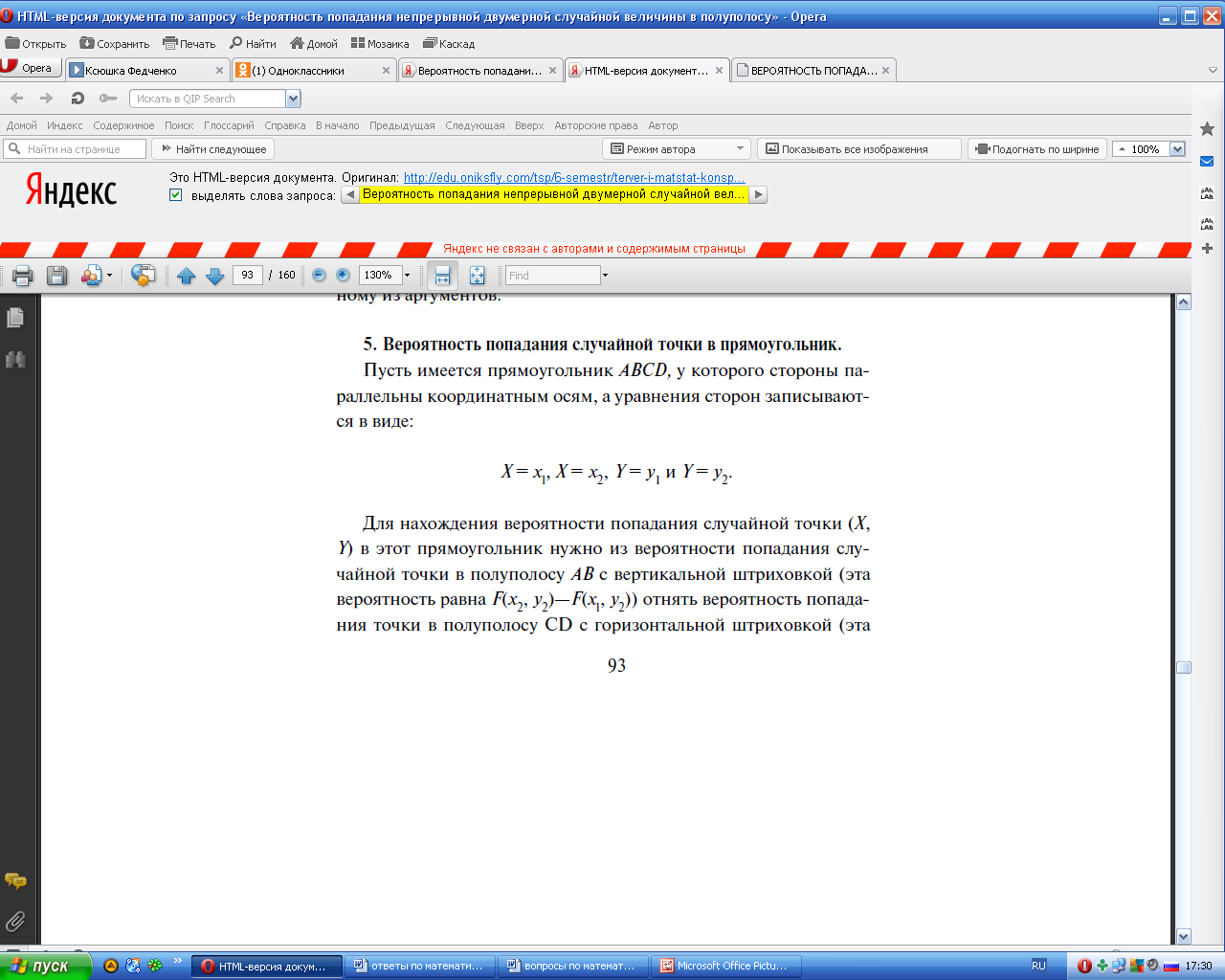
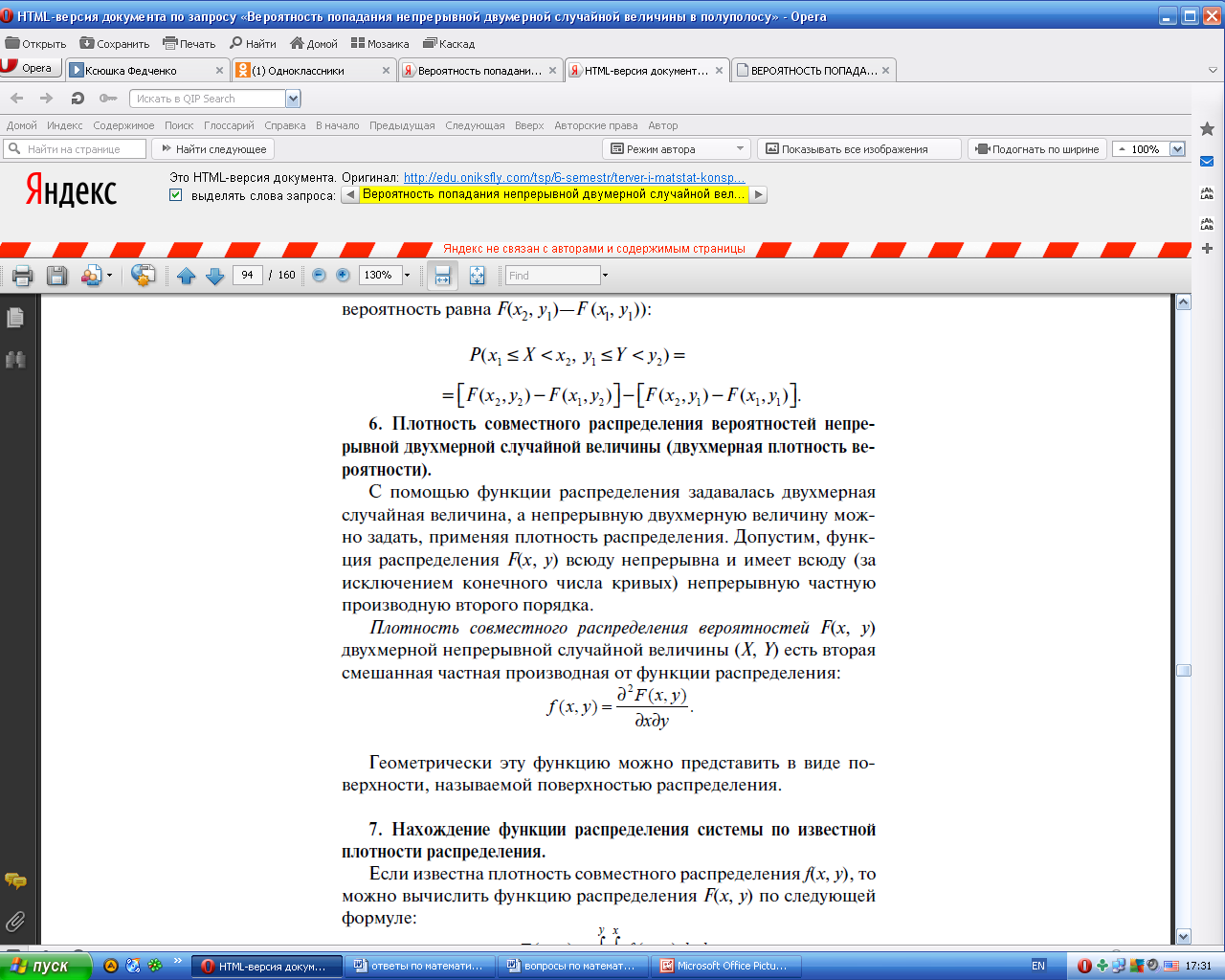
- •28.Вероятность попадания непрерывной двумерной случайной величины в полуполосу и прямоугольник.
- •30.Вероятность попадания двумерной случайной величины в произвольную область. Свойства нормировки для .
- •31.Отыскание составляющих двумерной случайной величины х и у , а также .
- •32.Необходимые и достаточные условия независимости случайных величин х и у.
- •33.Корреляционный момент случайных величин х и у. Формулы для его нахождения для дискретной случайной величины и непрерывной случайной величины.
- •34.Коэффициент корреляции, его свойства.
- •39.Метод наибольшего правдоподобия для определенных параметров непрерывной случайной величины. Метод моментов для их определения. Метод моментов для двух параметрических величин
Системы случайных величин (случайные векторы, двумерные случайные величины). Закон распределения дискретной двумерной случайной величины. Законы распределения ее составляющих х и у.
На практике нередко приходится одновременно учитывать значения нескольких величин, неслучайных и случайных. Это приводит к понятию системы случайных величин. Математически такую систему можно также называть многомерной случайной величиной или случайным вектором.
Случайный вектор (n-мерная случайная величина) представляет собой упорядоченную совокупность обычных (непрерывных или дискретных) случайных величин: X = (X1, X2,...,Xn ). Каждая координата (компонента) Xi имеет определенные математические характеристики (функции распределения, математическое ожидание, дисперсию.
Для задания всех вероятностей, связанных с парой (X,Y) дискретных случайных величин, используется таблица совместного распределения, которая имеет следующий вид:
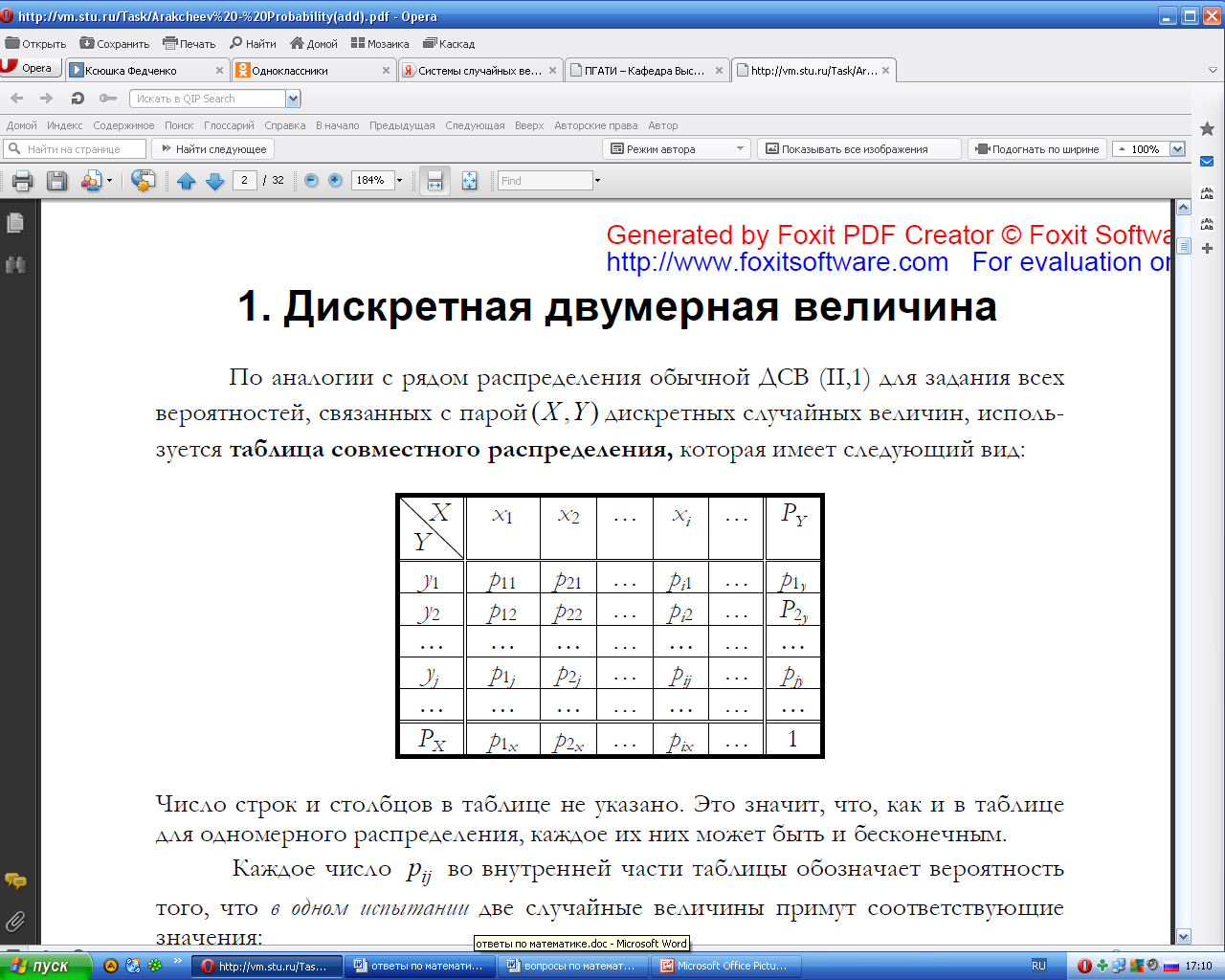
Имея закон распределения двумерной случайной величины можно получить законы распределения ее составляющий X и Y:
Х:
x |
x1 |
x2 |
… |
xn |
p |
p11+p12+…p1n |
p21+p22+…+p2n |
… |
pn |
28.Вероятность попадания непрерывной двумерной случайной величины в полуполосу и прямоугольник.
30.Вероятность попадания двумерной случайной величины в произвольную область. Свойства нормировки для .
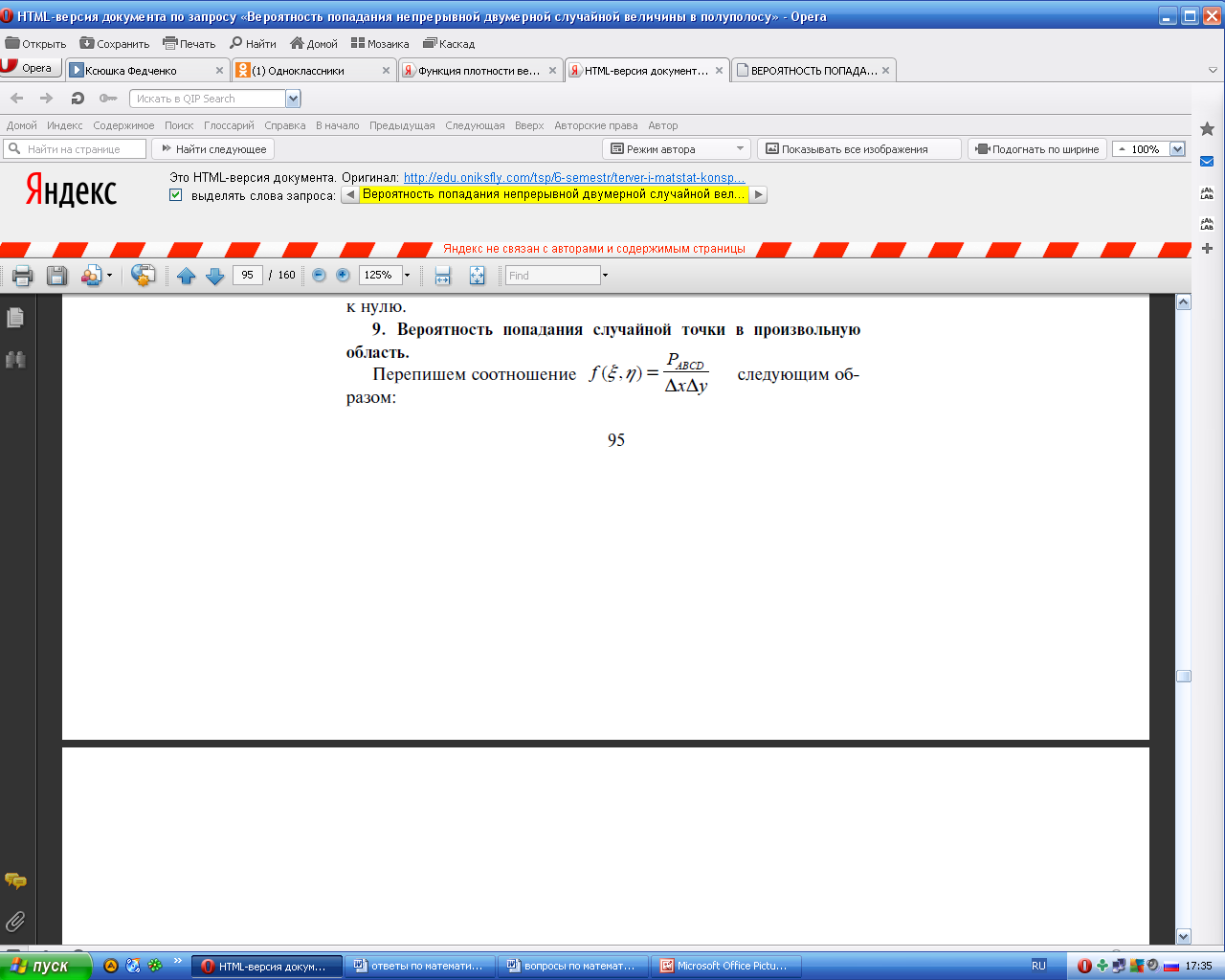
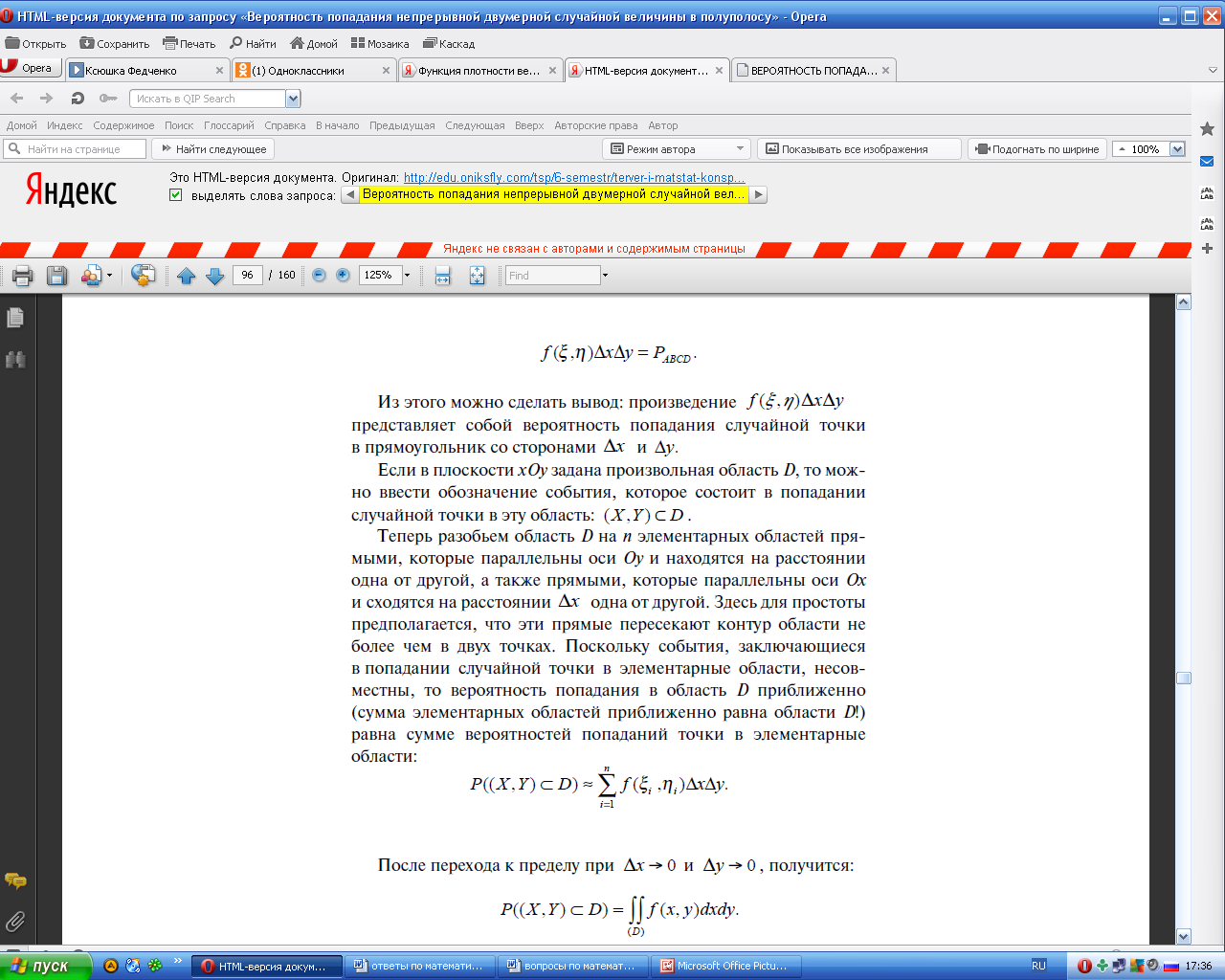

31.Отыскание составляющих двумерной случайной величины х и у , а также .
Допустим, мы знаем, чему равна плотность совместного распределения вероятностей системы двух случайных величин.
Для нахождения плотности распределения каждой из составляющих сначала нужно найти плотность распределения составляющей X. Пусть F1(x) есть функция распределения составляющей X. На основании определения плотности распределения одномерной случайной величины можно записать:
![]()
Учтем, что
![]() ,
,
![]() .
.
тогда
можно найти
![]()
Если продифференцировать обе части этого равенства по х, то получится
![]() или
или
![]() .
.
Таким же образом находится плотность распределения составляющей Y:
![]() .
.
Следовательно, плотность распределения одной из составляющих равна несобственному интегралу с бесконечными пределами от плотности совместного распределения системы. При этом переменная интегрирования соответствует другой составляющей.
32.Необходимые и достаточные условия независимости случайных величин х и у.
Для того чтобы случайные величины Х и Y были независимы, необходимо и достаточно, чтобы функция распределения системы (X, Y) была равна произведению функций распределения составляющих.
![]()
33.Корреляционный момент случайных величин х и у. Формулы для его нахождения для дискретной случайной величины и непрерывной случайной величины.
Корреляционным
моментом
![]() случайных величин Х и Y называется
математическое ожидание произведения
отклонений этих величин.
случайных величин Х и Y называется
математическое ожидание произведения
отклонений этих величин.
![]()
Практически используются формулы:
Для
дискретных случайных величин:
![]()
Для
непрерывных случайных величин:
![]()
Корреляционный момент служит для того, чтобы охарактеризовать связь между случайными величинами. Если случайные величины независимы, то их корреляционный момент равен нулю. Корреляционный момент имеет размерность, равную произведению размерностей случайных величин Х и Y.
