
- •Статистические и геометрические вероятности. Задача о встрече.
- •Перестановки. Число перестановок во множестве из n-элементов. Сочетания. Число сочетаний по k-элементам во множестве из n-элементов. Размещение. Примеры применения в подсчете их вероятностей.
- •Сумма событий. Теорема о сложении вероятностей несовместных событий. Произведение событий, условные вероятности. Теорема умножения вероятностей.
- •Полная группа событий. Противоположные события. Вероятность появления хотя бы одного события. Формула полной вероятности.
- •Формулы Бейеса. Вероятность суммы двух совместных событий.
- •Повторение испытаний. Формула Бернулли. Локальная теорема Муавра-Лапласа.
- •Повторение испытаний. Интегральная теорема Лапласа. Формула Пуассона.
- •Случайные величины. Дискретные и непрерывные случайные величины. Закон распределения. Дискретные случайные величины. Математическое ожидание дискретной случайной величины.
- •Вероятностный смысл математического ожидания дискретной случайной величины, его свойство.
- •Дисперсия дискретной случайной величины, свойство 3 дисперсии дискретной случайной величины.
- •Дисперсия дискретной случайной величины. Свойство 1-2 дисперсии. Среднеквадратическое отклонение. Геометрическое распределение. Гипергеометрическое распределение.
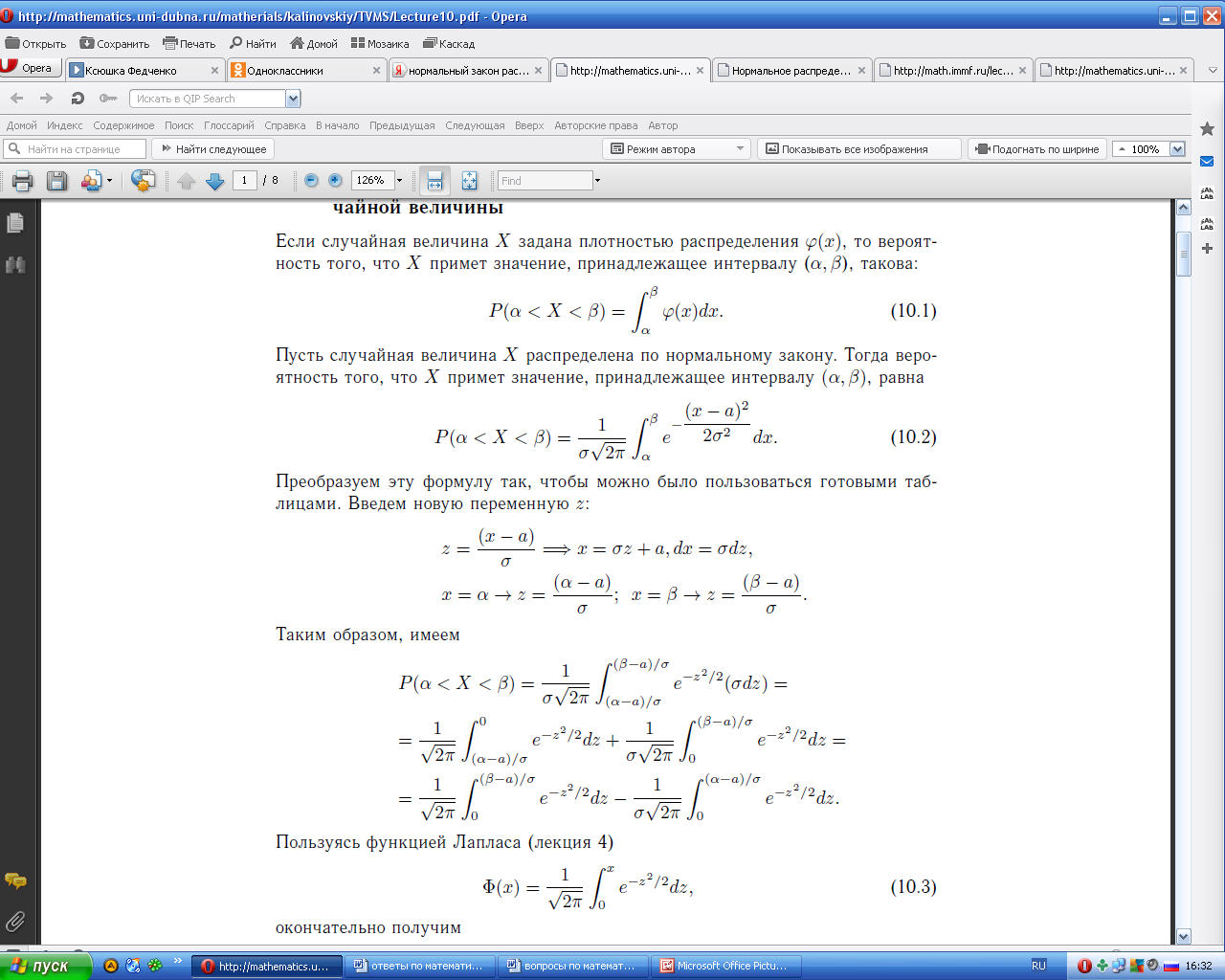
- •Вероятность попадания непрерывной случайной величины в заданный интервал. Плотность вероятности . Ее свойства.
- •Системы случайных величин (случайные векторы, двумерные случайные величины). Закон распределения дискретной двумерной случайной величины. Законы распределения ее составляющих х и у.
- •28.Вероятность попадания непрерывной двумерной случайной величины в полуполосу и прямоугольник.
- •30.Вероятность попадания двумерной случайной величины в произвольную область. Свойства нормировки для .
- •31.Отыскание составляющих двумерной случайной величины х и у , а также .
- •32.Необходимые и достаточные условия независимости случайных величин х и у.
- •33.Корреляционный момент случайных величин х и у. Формулы для его нахождения для дискретной случайной величины и непрерывной случайной величины.
- •34.Коэффициент корреляции, его свойства.
- •39.Метод наибольшего правдоподобия для определенных параметров непрерывной случайной величины. Метод моментов для их определения. Метод моментов для двух параметрических величин
Вероятность попадания непрерывной случайной величины в заданный интервал. Плотность вероятности . Ее свойства.
Вероятность
попадания непрерывной случайной величины
на отрезок от a
до b
определяется в виде
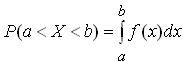
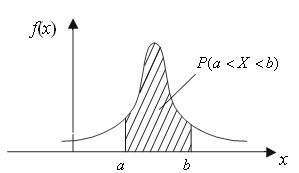
Геометрически вероятность попадания случайной величины X на участок (a, b) равна площади под кривой распределения, опирающейся на этот участок
Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f(x) – первую производную от функции распределения вероятностей F(X):
![]() .
.
Таким образом, функция распределения вероятностей является первообразной для плотности распределения вероятностей.
Теорема. Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу , равна определенному интегралу от плотности распределения, взятому в соответствующих пределах:
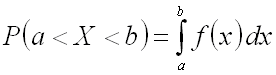
Свойства плотности распределения вероятностей
1. Плотность
распределения вероятностей –
неотрицательная функция:
![]() .
.
2. Несобственный
интеграл от плотности распределения
вероятностей в пределах от
![]() до
до
![]() равен единице:
равен единице:
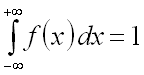 .
.
Нахождение по известной . Математическое ожидание непрерывной случайной величины.
Следовательно,
зная плотность распределения вероятности
f(x),
можно найти функцию распределения F(X)
по формуле
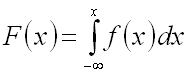 .
.
Математическим
ожиданием непрерывной случайной величины
X,
возможные значения которой принадлежат
отрезку
![]() ,
называют определенный интеграл
,
называют определенный интеграл
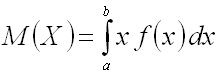 .
.
Если возможные
значения принадлежат всей числовой
оси, то
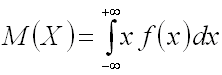
Дисперсия непрерывной случайной величины и среднеквадратическое отклонение.
Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.
Если возможные
непрерывной случайной величины X
принадлежат отрезку
,
то
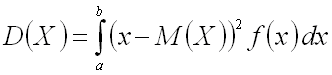 .
.
Если возможные значения принадлежат всей числовой оси, то
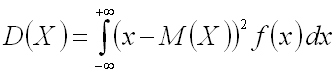
Среднеквадратическим отклонением непрерывной случайной величины называют, как и для величины дискретной, квадратный корень из дисперсии:
![]() .
.
Нормальный закон распределения непрерывной случайной величины, параметр
 этого распределения.
этого распределения.
Непрерывная случайная величина Х называется распределенной по нормальному закону, если ее плотность распределения равна
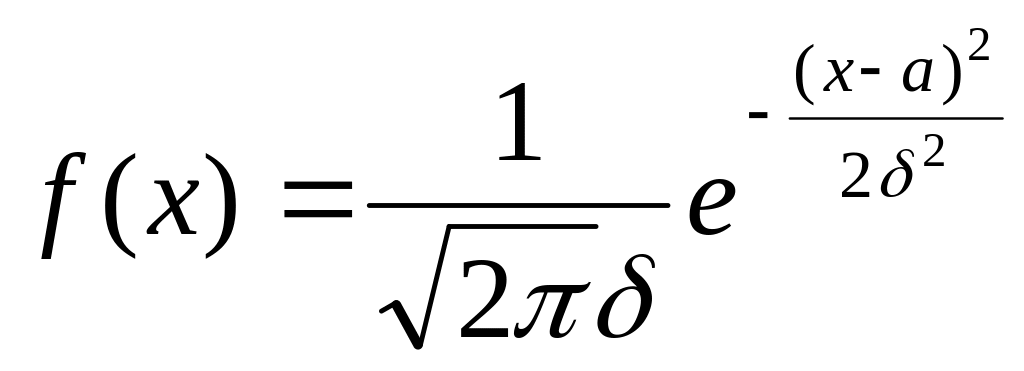
где a - математическое ожидание случайной величины;
Нормальный закон распределения непрерывной случайной величины, параметр
 этого
распределения.
этого
распределения.
Непрерывная случайная величина Х называется распределенной по нормальному закону, если ее плотность распределения равна
σ2 - дисперсия случайной величины, характеристика рассеяния значений случайной величины около математического ожидания.
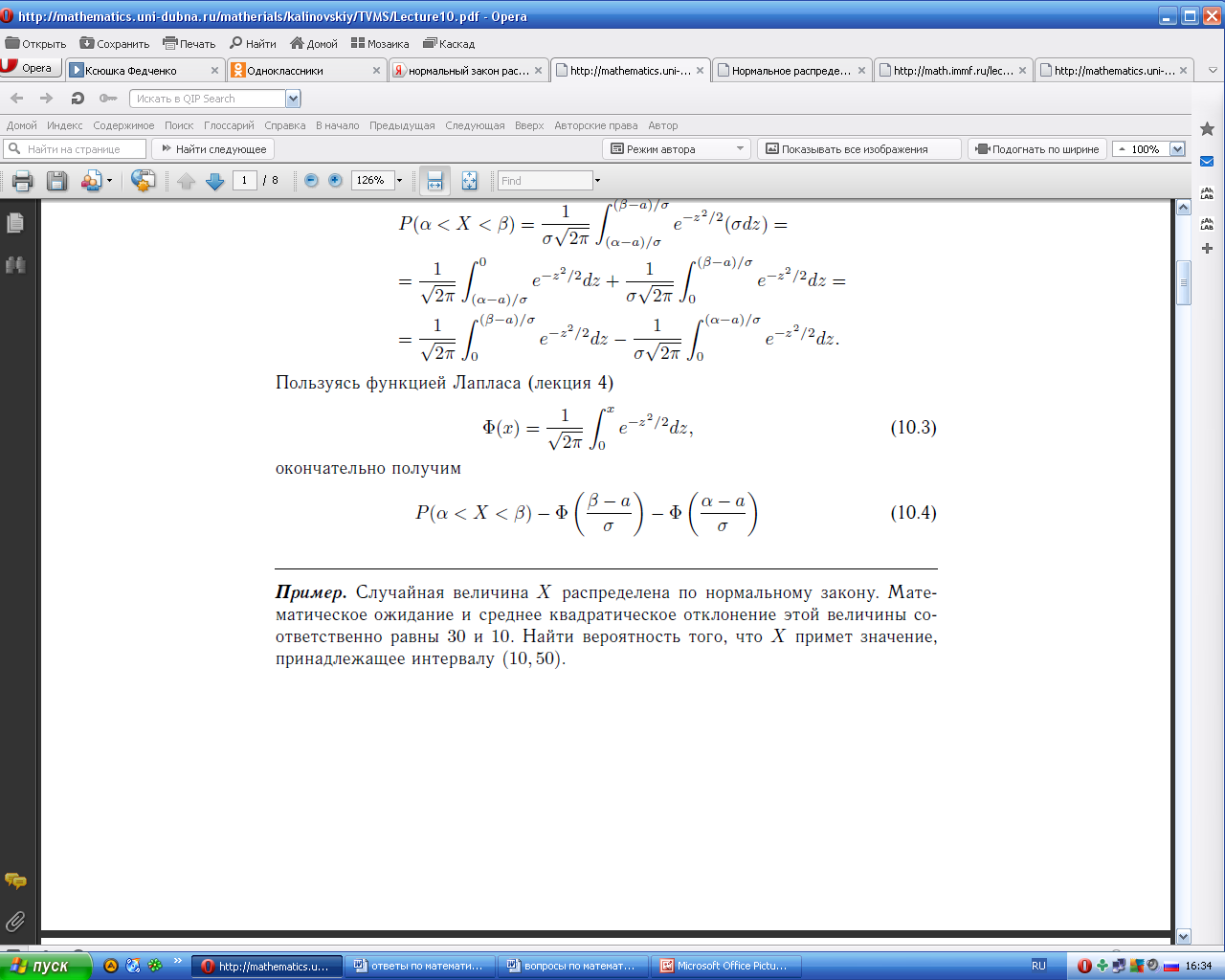
Кривая Гаусса. Вероятность попадания нормальной случайной величины в заданный интервал.
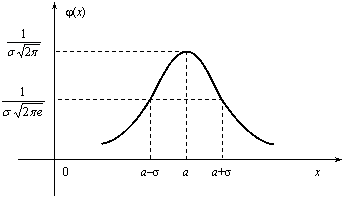
График дифференциальной
функции нормального распределения
называют нормальной кривой (кривой
Гаусса). Нормальная кривая симметрична
относительно прямой х =а, имеет максимальную
ординату
![]() ,
а в точках х = а ± σ – перегиб.
,
а в точках х = а ± σ – перегиб.
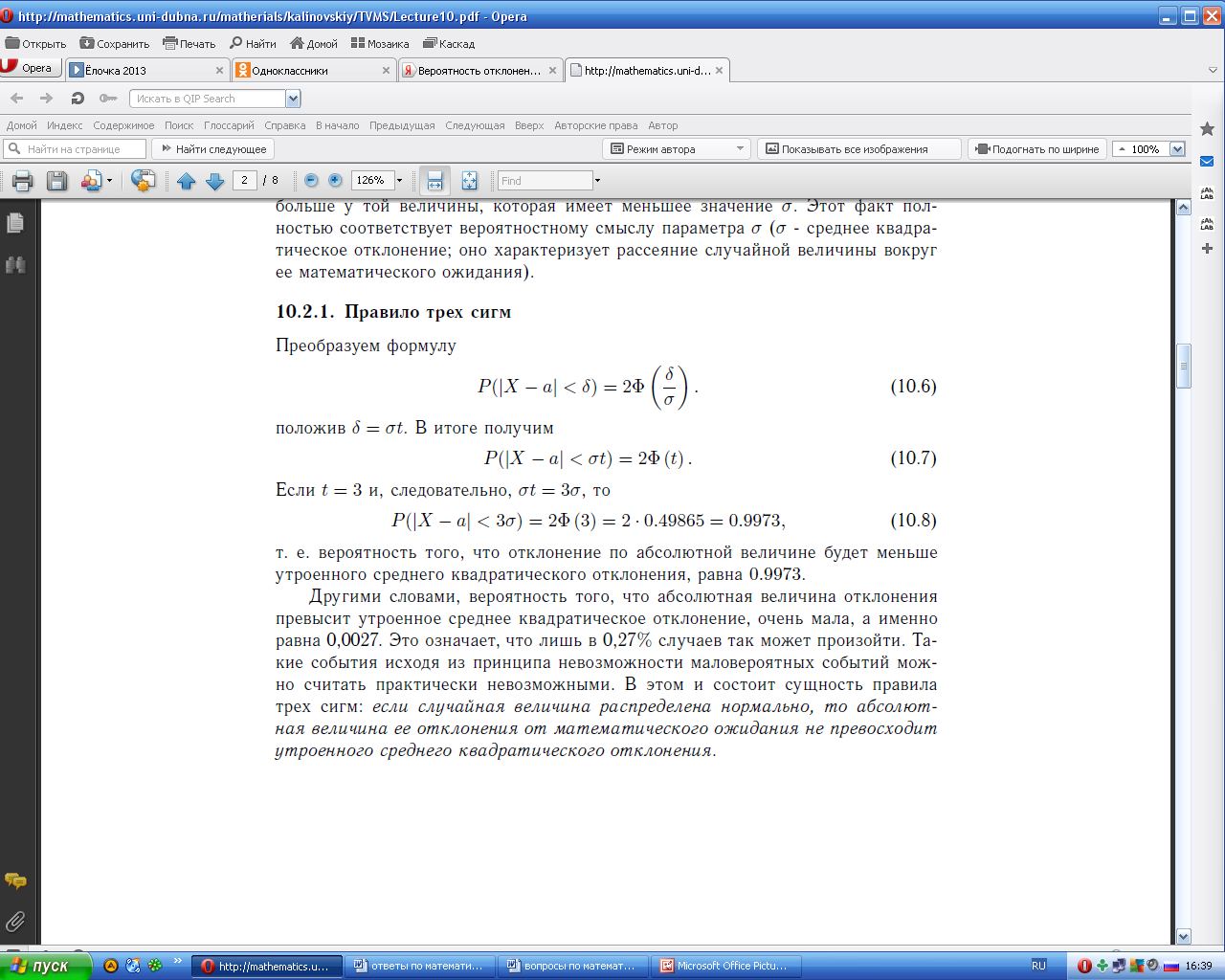
Вероятность отклонения нормальной случайной величины от ее математического ожидания. Правило трех .

Равномерное распределение. Показательное распределение. Равенство математического ожидания и среднеквадратического отклонения такого распределения.
Равномерное распределение
Случайная величина Х имеет равномерное распределение на интервале [a; b], если на этом интервале плотность вероятности случайной величины Х постоянна, а вне его равна нулю, т.е., если
![]()
где с - постоянная величина (c=const). Равномерное распределение иногда называют законом равномерной плотности.
Математическое ожидание и дисперсия непрерывной случайной величины Х, равномерно распределенной, соответственно равны
![]()
![]()
Случайная величина имеет экспоненциальное (показательное) распределение, если функция плотности распределения: X
![]() ,
где
,
где
![]()
Математическое
ожидание:![]()
Дисперсия:![]()
Экспоненциальное
распределение является однопараметрическим
с параметром
![]() ,
причем:
,
причем:![]()
