10. Вероятностный смысл математического ожидания дискретной случайной величины, его свойство.

Математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины. Равенство будет тем точнее, чем больше число испытаний.

Математическое ожидание больше наименьшего и меньше наибольшего возможных значений. Поэтому можно сказать, что математическое ожидание характеризует положение случайной величины на числовой оси, т.е. указывает некоторое среднее значение, около которого группируются все возможные значения случайной величины. Такое среднее значение является «представителем» случайной величины и может замещать ее при грубых оценочных расчетах.

Свойства математического ожидания случайной величины:

1.Математическое ожидание постоянной величины равно самой величине:

М[C]=C.

2.Постоянный множитель можно выносить за знак математического ожидания:

М[C×Х]=C×M[X].

3.Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий этих величин:

М[Х+Y]=M[X]+M[Y].

4.Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин:

М[Х×Y]=M[X]×M[Y].

(Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения принимает другая величина.)

11. Дисперсия дискретной случайной величины, свойство 3 дисперсии дискретной случайной величины.

Дисперсия дискретной случайной величины есть математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

свойство 3: дисперсия произведения двух независимых случайных величин является произведением их дисперсий. Для расчета дисперсий случайных величин часто применяется формула:

12. Дисперсия дискретной случайной величины. Свойство 1-2 дисперсии. Среднеквадратическое отклонение. Геометрическое распределение. Гипергеометрическое распределение.

Дисперсия дискретной случайной величины есть математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

Свойства дисперсии.

1) Дисперсия постоянной величины равна нулю: D(С) = 0

2) Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(СХ) = С² · D(Х)

3) Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых: D(Х1 ± Х2 ± ... ± Хn) = D(Х1) + D(Х2) + ... + D(Хn)

Среднеквадратическое отклонение дискретной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии:

σ(X) = √D(X)

Геометрическое рапределение

Производится серия испытаний. Случайная величина - количество испытаний до появления первого успеха (например, бросание мяча в корзину до первого попадания). Закон распределения имеет вид:

Если количество испытаний не ограничено, т.е. если случайная величина может принимать значения 1, 2, ..., ∞, то математическое ожидание и дисперсию геометрического распределения можно найти по формулам M(X) = 1/p, D(X) = q/p²

Гипергеометрическое распределение

Имеется N объектов. Из них n объектов обладают требуемым свойством. Из общего количества отбирается m объектов. Случайная величина X - число объектов из m отобранных, обладающих требуемым свойством. Для вычисления вероятностей используются биномиальные коэффициенты (см. число сочетаний). Закон распределения имеет вид:

13. Математическое ожидание, дисперсия, среднеквадратическое отклонение биномиального распределения.

Биномиальным называют закон распределения дискретной случайной величины X - числа появлений события в n независимых испытаниях, в каждом из которых вероятность наступления события постоянна. Вероятности p_i вычисляют по формуле Бернулли

Для биномиального распределения:

математическое ожидание M(X) = np,

дисперсия D(X) = npq,

среднеквадратическое отклонение σ=√npq.

14. Неравенство Чебышева.

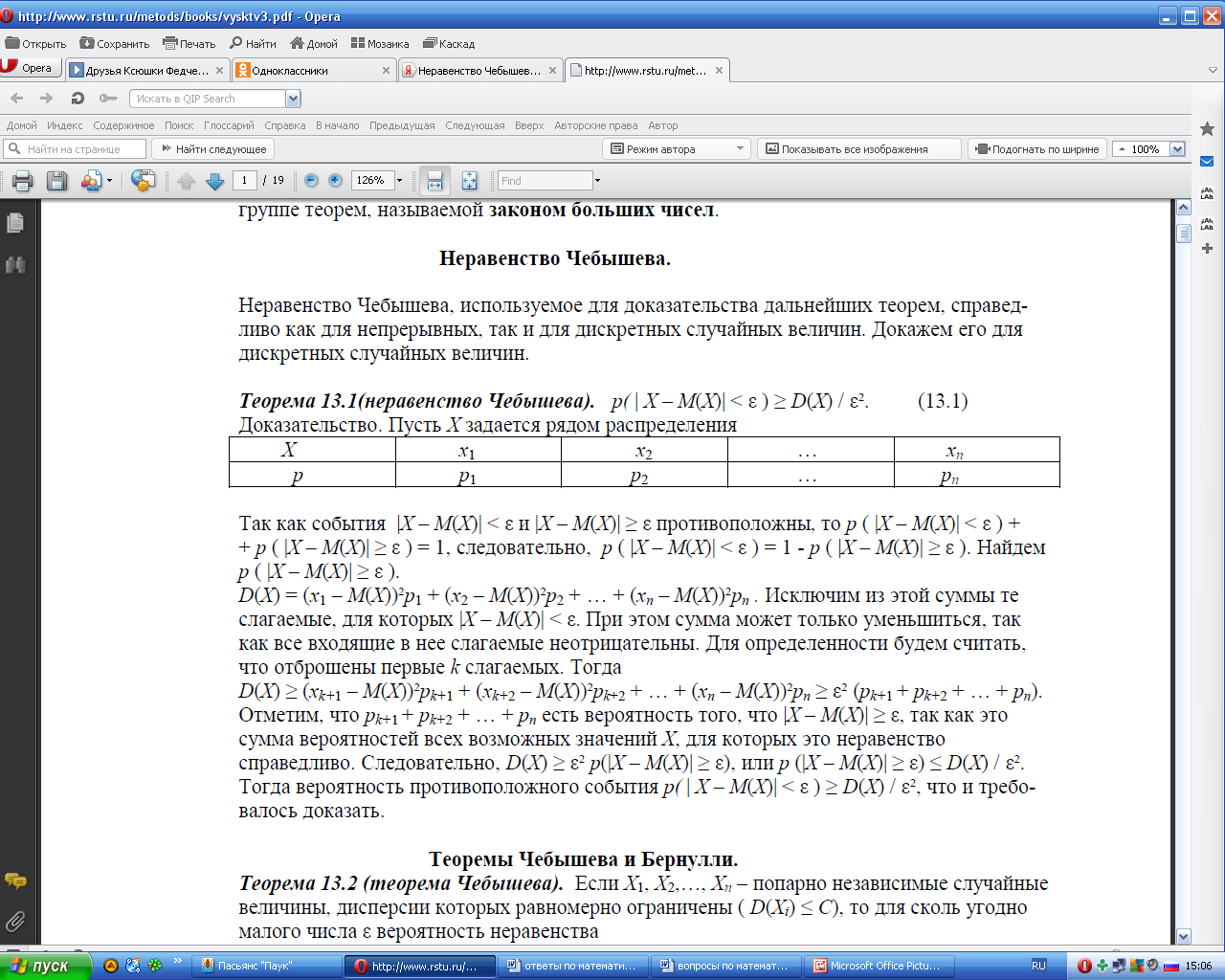
15. Теорема Чебышева.

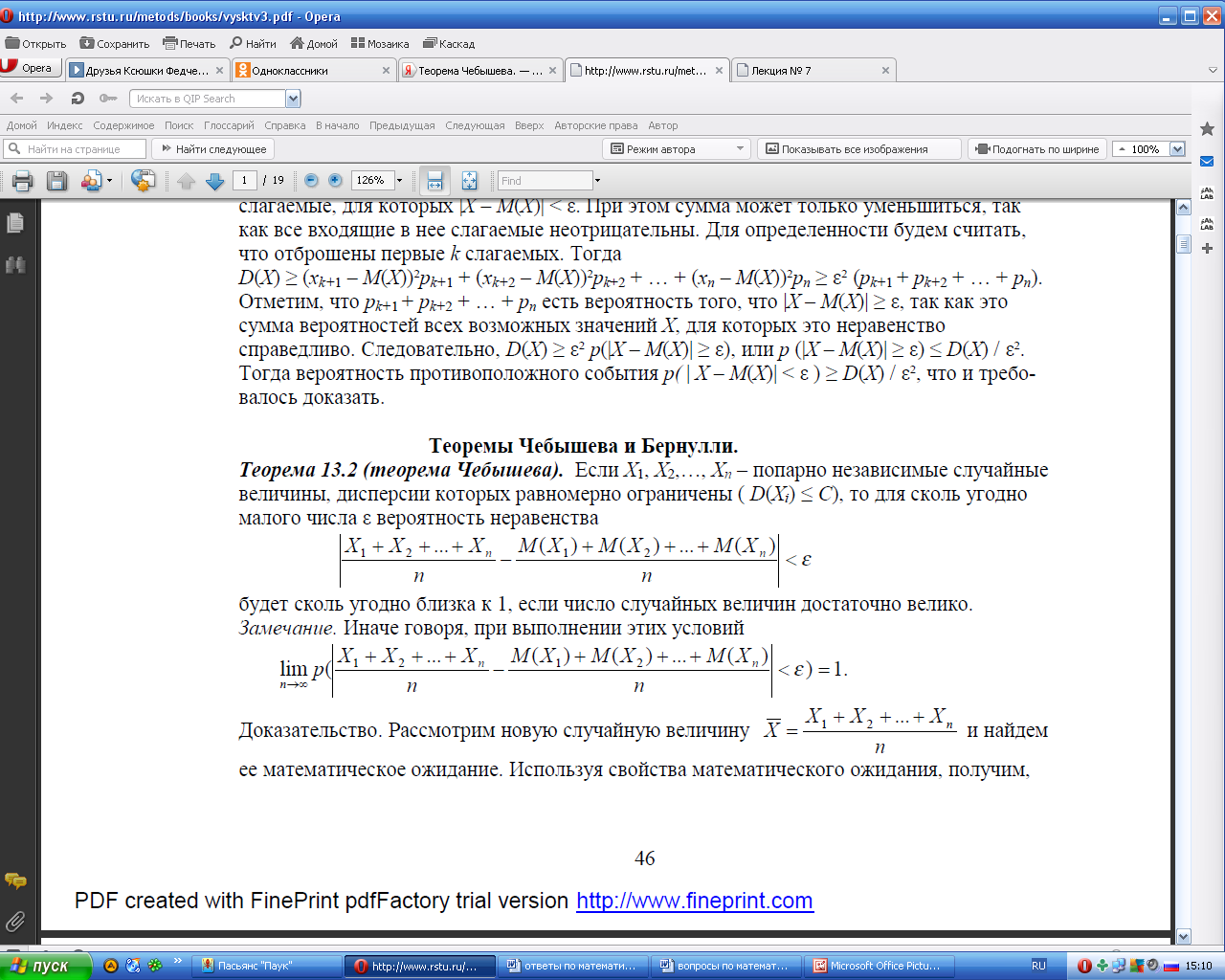
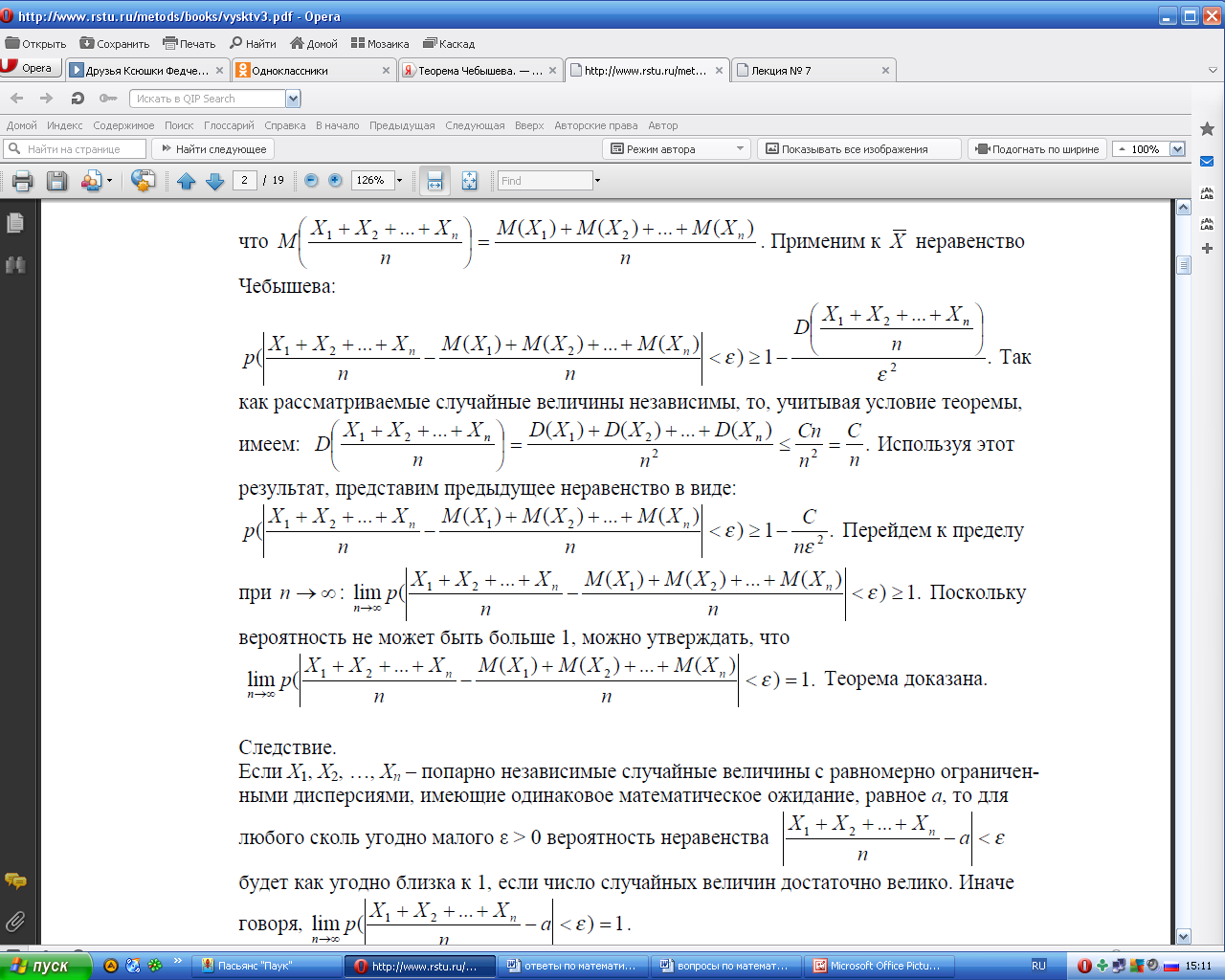
16. Частный случай теоремы Чебышева. Теорема Бернулли. Значение закона больших чисел для практики.

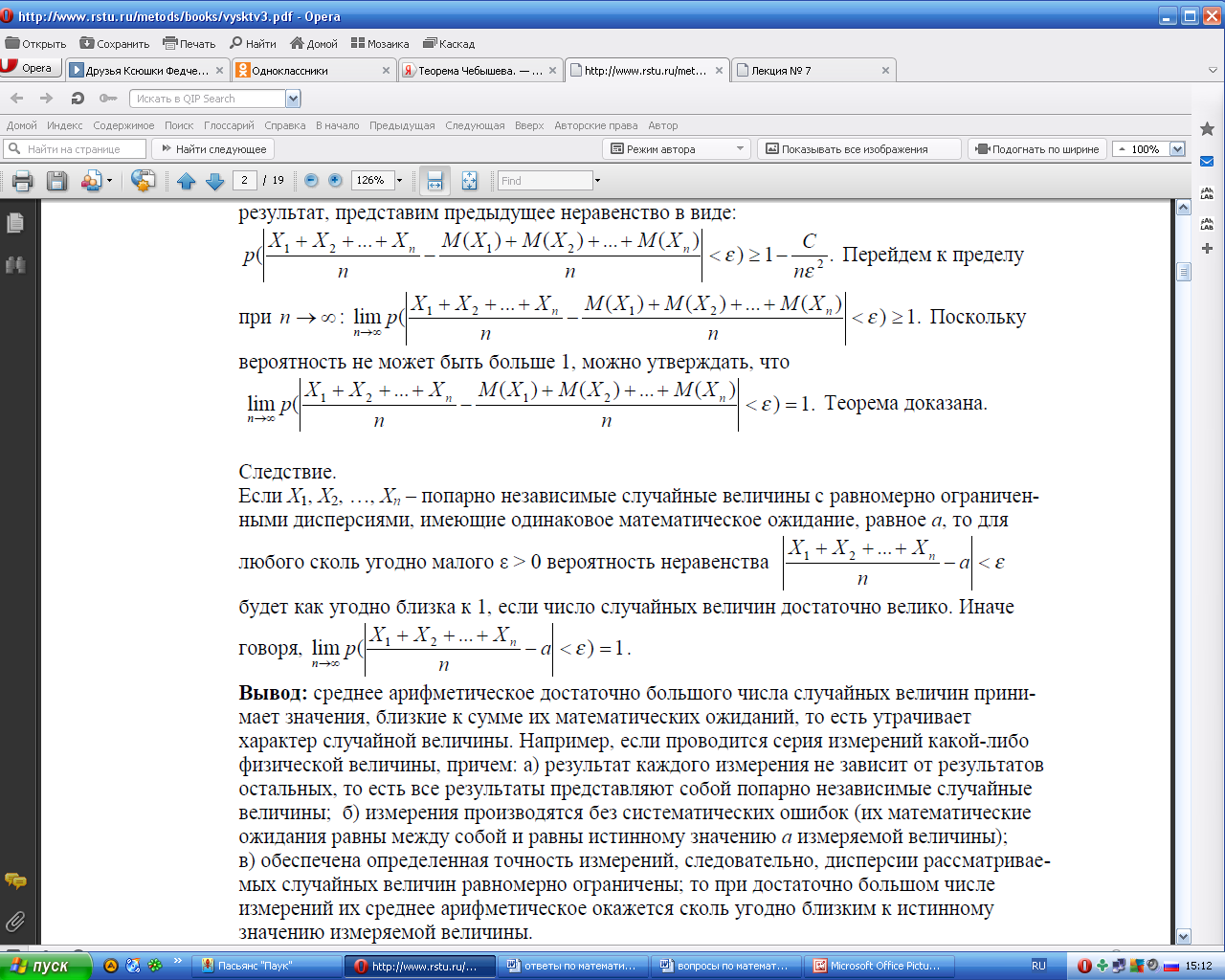
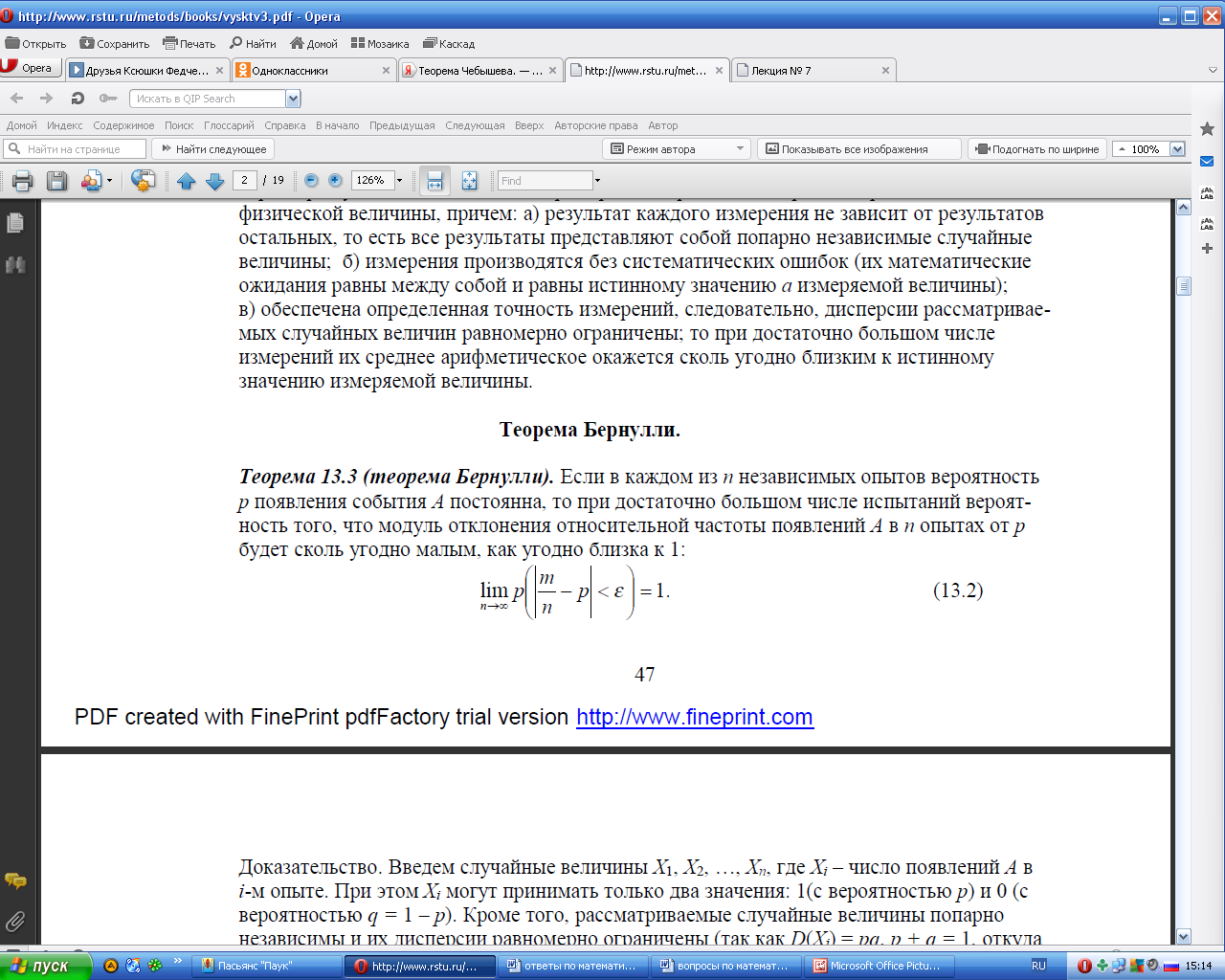
Общий смысл закона больших чисел - совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.

17. Случайная непрерывная величина. Функция распределения случайной непрерывной величины 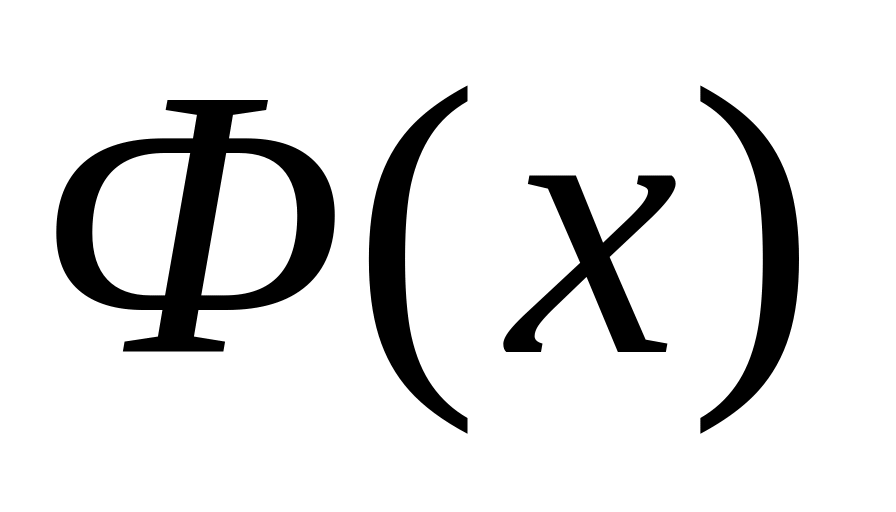. Ее свойства. Вероятностный смысл.

Функцией распределения вероятностей называют функцию F(X), определяющую вероятность того, что случайная величина в результате испытания примет значение, меньшее x, то есть:

.

Случайную величину называют непрерывной, если ее функция распределения вероятностей есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.

Функция распределения непрерывной случайной величины Х с плотностью распределения f(x) определяется в виде 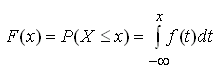для .

Свойства функции распределения вероятностей случайной величины

1. Значения функции распределения вероятностей принадлежат отрезку :

2. Функция распределения вероятностей – неубывающая функция, то есть: , если .

3. Если возможные значения непрерывной случайной величины принадлежат интервалу , то:

, если ;

, если .