6. Формулы Бейеса. Вероятность суммы двух совместных событий.

Предположим, что производится некоторый опыт, причем об условиях его проведения можно высказать n единственно возможных и несовместных гипотез , имеющих вероятности . Пусть в результате опыта может произойти или не произойти событие А, причем известно, что если опыт происходит при выполнении гипотезы , то

Спрашивается, как изменятся вероятности гипотез, если стало известным, что событие А произошло? Иными словами, нас интересуют значения вероятностей .

откуда

Но по формуле полной вероятности

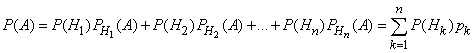
Поэтому

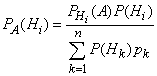
Формула называется формулой Бейеса.

Вероятность суммы двух совместных событий А и В равна сумме их вероятностей без вероятности их совместного появления, т.е. Р(А+В)=Р(А)+Р(В)-Р(АВ).

Доказательство:

Всего исходов N, благоприятствующих событию А- К, событию В- L, совместному появлению А и В- М. Следовательно, благоприятных исходов для события А+В : K+L-M. Откуда вероятность события А+В:

7. Повторение испытаний. Формула Бернулли. Локальная теорема Муавра-Лапласа.

Пусть производится n независимых испытаний, в каждом из которых событие A может появиться с постоянной вероятностью p и не появиться с постоянной вероятностью (1-p)=q.

Найти вероятность того, что в n испытаниях случайное событие наступит ровно k раз.

- формула Бернулли.

Теорема Муавра- Лапласа: Если вероятность наступления события А в каждом из n независимых испытаниях равна р и отлична от 0 и единицы, а число испытаний достаточно велико, то вероятность того, что в n испытаниях событие А наступит k раз, приближенно равна значению функции

где ,

Значение функции можно найти в "Таблице значений функции ". При этом нужно учитывать, что функция четная. При x>4 значение функции принимается равным нулю.

8. Повторение испытаний. Интегральная теорема Лапласа. Формула Пуассона.

Интегральная теорема Муавра-Лапласа: Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие А появится в n испытаниях от k1 до k2 раз. Приближенно равна определенному интегралу

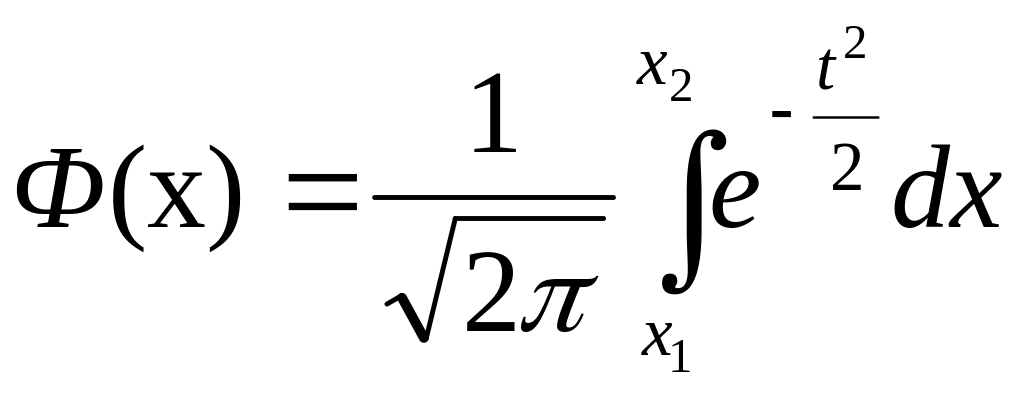где

Данный интеграл называется функцией Лапласа

Ф(х)- нечетная функция, значения ее приведены в "Таблице значений функции Ф(х). При x>5 принимают Ф(х)=0,5.

Формула Пуассона. Если вероятность p наступления события A в каждом испытании постоянна и мала, а число независимых испытаний n достаточно велико, то вероятность наступления события ровно раз приближенно равна

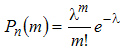, где .

Доказательство. Пусть даны вероятность наступления события A в одном испытании p и число независимых испытаний n. Обозначим . Откуда . Подставим это выражение в формулу Бернулли:

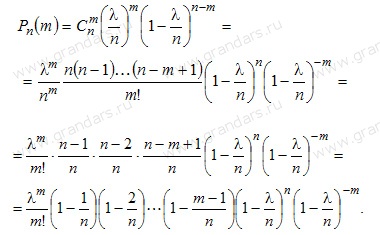
При достаточно большом n, и сравнительно небольшом m, все скобки, за исключением предпоследней, можно принять равными единице, т.е.

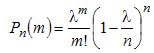
Учитывая то, что n достаточно велико, правую часть этого выражения можно рассмотреть при , т.е. найти предел

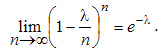
Тогда получим

9. Случайные величины. Дискретные и непрерывные случайные величины. Закон распределения. Дискретные случайные величины. Математическое ожидание дискретной случайной величины.

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Дискретной случайной величиной (ДСВ) называют такую величину, множество значений которой либо конечное, либо бесконечное, но счетное.

Непрерывной случайной величиной (НСВ) называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Множество возможных значений непрерывной случайной величины бесконечно и несчетно.

случайные величины могут иметь одинаковые перечни возможных значений, а вероятности их появления — различные. Поэтому для задания дискретной случайной величины недостаточно перечислить все возможные ее значения, нужно еще указать их вероятности.

Заданное соответствие между возможными значениями ДСВ и их вероятностями называется законом распределения дискретной случайной величины; его можно задать таблично

x	x1	x2	…	xn
p	p1	p2	…	pn

При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая - их вероятности.

Приняв во внимание, что в одном испытании случайная величина принимает одно и только одно возможное значение, заключаем, что события образуют полную группу; следовательно, сумма вероятностей этих событий, т. е. сумма вероятностей второй строки таблицы, равна единице:

Математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины. Математическое ожидание ДСВХ равно сумме произведений всех ее возможных значений на их вероятности, т.е.