1. События. События независимые, несовместные, невозможные, достоверные, случайные, равновозможные. Классическое определение вероятности. Границы применимости классического определения вероятности. Ошибка Даламбера.

Испытанием или опытом называется осуществление какого-нибудь определенного комплекса условий, который может быть воспроизведен сколь угодно большое число раз. Случайным называется событие, которое может произойти или не произойти в результате некоторого испытания (опыта). Таким образом, событие рассматривается как результат испытания.

Наблюдаемые нами события различаются по степени возможности их появления и по характеру их взаимосвязи. Событие называется достоверным, если оно обязательно произойдет в результате данного испытания. Событие называется невозможным, если оно не может произойти в результате данного испытания. Два или несколько событий называются равновозможными в данном испытании, если имеются основания считать, что ни одно из этих событий не является более возможным или менее возможным, чем другие.Два события называются несовместными в данном испытании, если появление одного из них исключает появление другого, и совместными в противном случае. Несколько событий образуют полную группу событий в данном испытании, если в результате этого испытания обязательно наступит хотя бы одно из них. Два несовместных события, образующих полную группу событий в данном испытании, называются противоположными событиями.

Вероятность события – численная мера возможности его наступления.

Если n – число всех случаев, а m – число случаев, благоприятствующих событию А, то вероятность события А определяется равенством:

Границы применения классического определения вероятности:

1.все исходы в нем предполагаются равновозможными.

2.в классическом определении числа возможных и благоприятствующих исходов предполагаются конечными.

Опыт (ошибка Даламбера): подбрасываем две одинаковые монеты. Какова вероятность того, что монеты упадут на одну и ту же сторону.

Решение Даламбера: Опыт имеет три равновозможных исхода:

1. обе монеты упали на «орла»;

2. обе монеты упали на «решку»;

3. одна из монет упала на «орла», другая на «решку».

Из них благоприятными для нашего события будут два исхода.

Правильное решение: Опыт имеет четыре равновозможных исхода:

1. первая монета упала на «орла», вторая тоже на «орла»;

2. первая монета упала на «решку», вторая тоже на «решку»;

3. первая монета упала на «орла», а вторая на - «решку»;

4. первая монета упала на «решку», а вторая на - «орла».

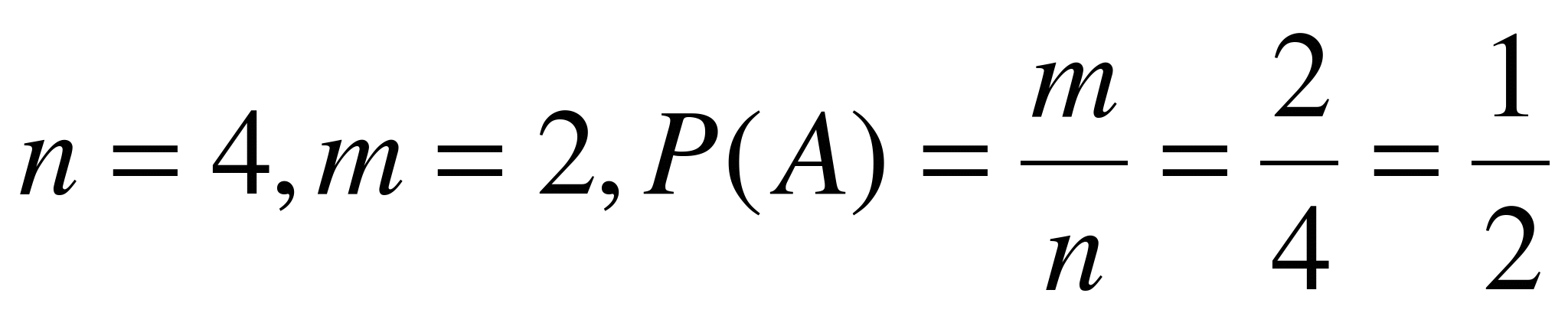
Даламбер допустил одну из самых распространенных ошибок: он объединил два элементарных исхода в один, тем самым, сделав его не равным по вероятности оставшимся исходам.

2. Статистические и геометрические вероятности. Задача о встрече.

При рассмотрении результатов отдельных испытаний очень трудно найти какие-либо закономерности. Однако в последовательности одинаковых испытаний можно обнаружить устойчивость некоторых средних характеристик. Относительной частотой какого-либо события в данной серии из n испытаний называется отношение m/n, числа m тех испытаний, в которых событие А наступило, к общему числу испытаний n. Почти в каждой достаточно длинной серии испытаний относительная частота события А устанавливается около определенного значения , которое принимается за вероятность события А. Устойчивость значения относительной частоты подтверждается специальными экспериментами. Статистические закономерности такого рода были впервые обнаружены на примере азартных игр, т. е. на примере тех испытаний, которые характеризуются равновозможностью исходов. Это открыло путь для статистического подхода к численному определению вероятности, когда нарушается условие симметрии эксперимента.

Геометрическое определение вероятности.

Задача о встрече

Двое договорились встретиться в определённом месте между двумя и тремя часами дня. Пришедший первым ждет другого в течение 10 минут, после чего уходит. Чему равна вероятность встречи?

Решение:

Будем считать интервал с 14 до 15 часов отрезком [0, 1] длиной в 1 час. Пусть Х и У— моменты прихода. Все возможные результаты эксперимента — точки квадрата со стороной 1.

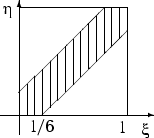
Можно считать, что эксперимент сводится к бросанию точки наудачу в квадрат. При этом благоприятными исходами являются точки множества А :

(10 минут = 1/6 часа).

Попадание в множество А наудачу брошенной в квадрат точки означает, что Х и У встретятся. Тогда вероятность встречи равна

3. Перестановки. Число перестановок во множестве из n-элементов. Сочетания. Число сочетаний по k-элементам во множестве из n-элементов. Размещение. Примеры применения в подсчете их вероятностей.

Размещением из n элементов по k (k ≤ n) называется любое упорядоченное подмножество из k элементов множества, состоящего из n различных элементов.

Пример. Следующие последовательности цифр являются размещениями по 2 элемента из 3 элементов множества {1;2;3}: 12, 13, 23, 21, 31, 32.

Число различных размещений из n элементов по k обозначается и вычисляется по формуле:

Перестановками из n элементов называются такие размещения из n элементов, которые различаются только расположением элементов.

Число перестановок из n элементов вычисляется по формуле:

Пример. Сколькими способами могут встать в очередь 5 человек? Количество способов равно числу перестановок из 5 элементов, т.е.

P5=5!=1∙2∙3∙4∙5=120.

Сочетаниями из n элементов по k называются такие размещения из n элементов по k, которые одно от другого отличаются хотя бы одним элементом.

Число различных сочетаний из n элементов по k обозначается и вычисляется по формуле: .

Пример. Имеются 5 цветков разного цвета. Для букета выбирается 3 цветка. Число различных букетов по 3 цветка из 5 равно: .