27.Устойчивость замкнутых линейных цепей. Условие и критерии устойчивости.

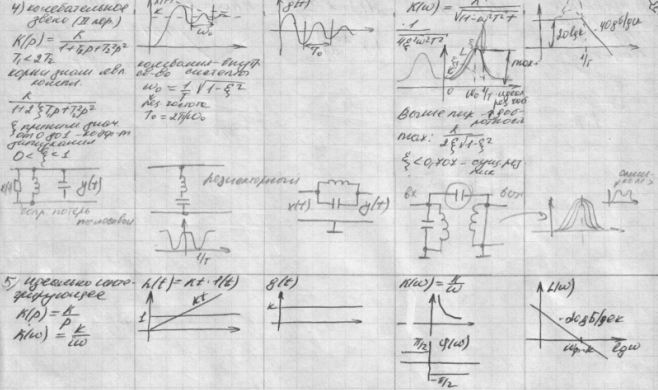
28.Замкнутые следящие системы. Система фазовой автоподстройки частоты. Дифференциальное уравнение системы фапч. Применение в системах передачи данных.

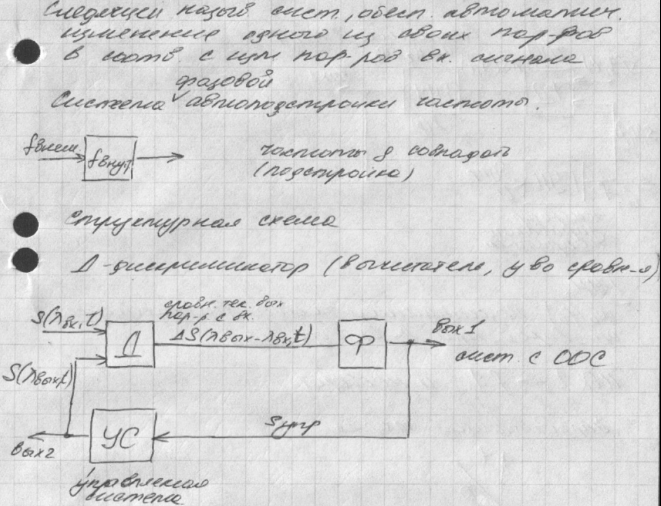
Принцип работы: Д сравнивает вых пар-р УС с вх параметром, ийот выполняет роль уставки и создает системные ошибки АS, ийот в зависимости от разности вх и вых параметров Ф выдел из сигнала очень полезную инфотрмацию сост-щую Sупр, ийот подается на вх упр сист. Под действие упр сигнала вых параметр λ вых изм так чтобы понизить ошибку. Существенное ограничение: следящая система явл инерционной работает только при изменении входных параметров в определенных пределах и с другой частотой(омега)

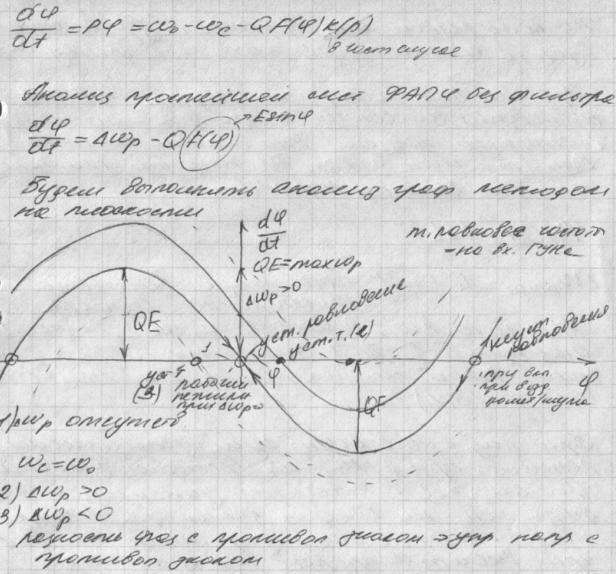
29.Анализ системы фапч без фильтра. Устойчивое и неустойчивое равновесие системы. Работа системы фапч в режиме захвата (слежения). Свойства и характеристики системы фапч.

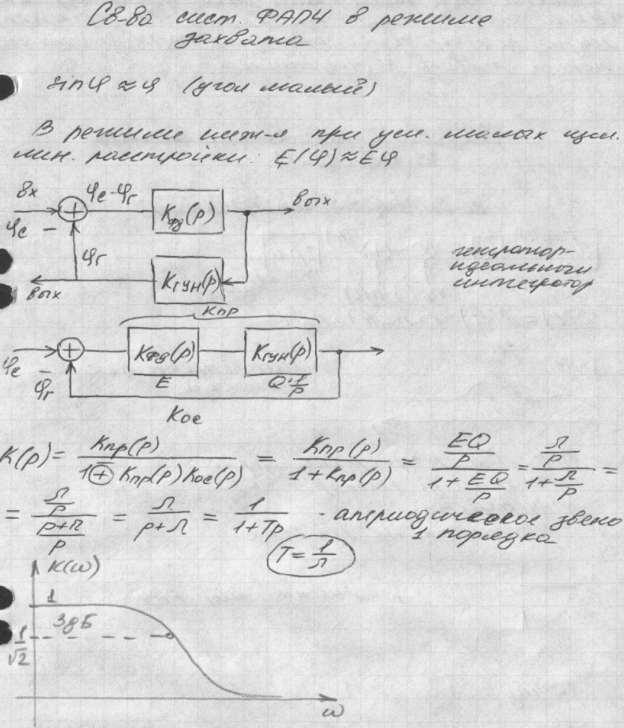
30.Представление помехи в виде случайного процесса. Стационарные и эргодические процессы. Статистические свойства случайных процессов. Одно-, двух-, и многомерные плотности вероятности и их числовые характеристики.

Случайный процесс ξ(t) называется стационарным в узком смысле

(или строго стационарным), если его функция распределения Wn(x1,x2…xn, t1, t2, …tn) произвольного порядка n не меняется при любом

сдвиге всей группы точек t1, t2… tn вдоль временной оси (для любых n и τ),

т.е Wn(x1,x2,…xn,t1,t2,…tn)=Wn(x1,x2,…xn,t1-t`,t2-t`,…tn-t`)

Другими словами, случайный процесс будет строго стационарным, если

выражения для функций распределения любого порядка не зависят от

положения начала отсчета времени.

Если вероятностные характеристики случайного процесса не

инвариантны по отношению к произвольному смещению начала отсчета

времени, то процесс – нестационарный.

Из приведенного определения следует, что для стационарного

случайного процесса:

- одномерная функция распределения имеет один и тот же вид в любой

момент времени (т.е. не зависит от времени) W1(x,t)=W1(x,t-t`)=W1(x)

- двумерная функция распределения может зависеть лишь от разности t2-t1

W2(x1,x2,t1,t2)=W2(x1,x2,t2-t1);

- трехмерная функция распределения может зависеть лишь от двух

Разностей t2-t1 b t3-t1, т.е. W3(x1,x2,x3,t1,t2,t3)=W3(x1,x2,x3,t2-t1,t3-t1)и т.д.

Так как одномерные функции распределения стационарных случайных

процессов не зависят от времени, то среднее значение и дисперсия этих

процессов не зависят от времени. Поскольку двумерная функция

распределения зависит только от разности t`=t2-t1, то и корреляционная

функция такого процесса зависит от одного временного параметра t`: B2(t`)= инт. инт. x1*x2*W2(x1,x2,t`)dx1,dx2

Случайные процессы, у которых среднее значение и дисперсия не

зависят от времени, а корреляционная функция второго порядка зависит

только от одного временного параметра, называются стационарными в

широком смысле. Следует отметить, что стационарность в широком смысле

не тождественна строгой стационарности. Случайные процессы,

стационарные строго, всегда стационарны в широком смысле, но не

наоборот. Эргодические случайные процессы А.Я.Хинчиным установлено свойство эргодичности у стационарных случайных процессов. Эргодическими процессами называют такие стационарные случайные процессы вероятностные характеристики которых, полученные по ансамблю реализаций в какой - либо момент времени (в одном сечении), с вероятностью, сколь угодно близкой к единице, совпадают с аналогичными

характеристиками, полученными усреднением по времени на одной

единственной реализации за достаточно большой промежуток.

Условием эргодичности стационарного случайного процесса является

требование, чтобы функция корреляции процесса с увеличением t`=t2-t1

стремилась к нулю.

Из эргодичности случайных процессов следует возможность

ограничится при вычислении моментных функций только одной

реализацией процесса:

31.Спектральные и корреляционные характеристики случайных процессов и связь между ними. Спектральная плотность мощности. Формула Винера-Хинчина. Энергетическая ширина спектра и интервал корреляции. Белый шум и его характеристики.

32.Нормальный случайный процесс. Причины широкого распространения. Центральная предельная теорема Ляпунова. Нормализация случайного процесса при прохождении через инерционную линейную цепь.

Теорема Ляпунова (центральная предельная теорема)

Если случайная величина складывается из множества других независимых случайных величин, то у этой случайной величины распределение нормально (Гауссовское).

33.Огибающая и фаза смеси сигнала и случайного процесса. Распределение огибающей. Законы Рэлея и Райса.

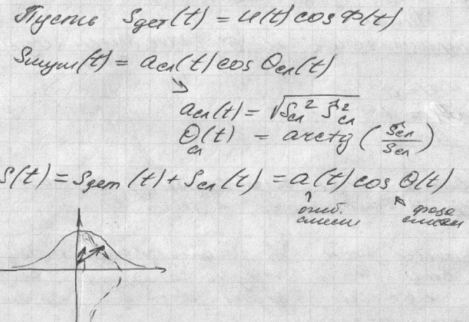
34.Распределение фазы смеси сигнала и случайного процесса. Зависимость распределений огибающей и фазы от отношения сигнал-шум.

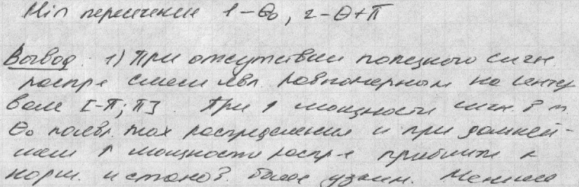
4Вещественный и комплексный сигналы.

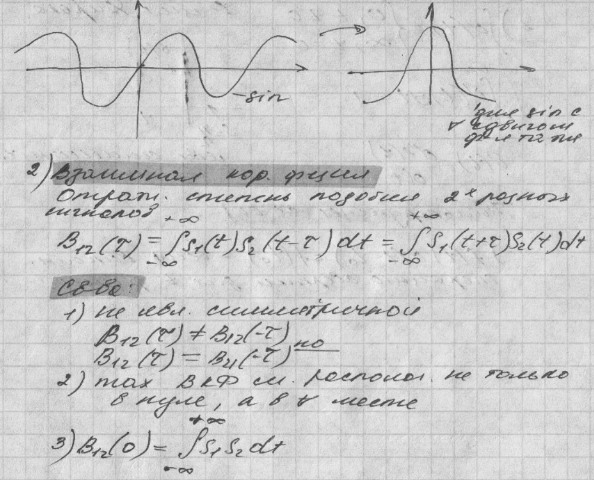
7.Коррляционные хар-ки синг.Авто- и взаимная корр-я, их свойства

5.Разложение в обобщенный ряд Фурье.

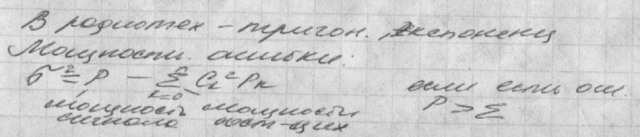
11.аналитический сигна

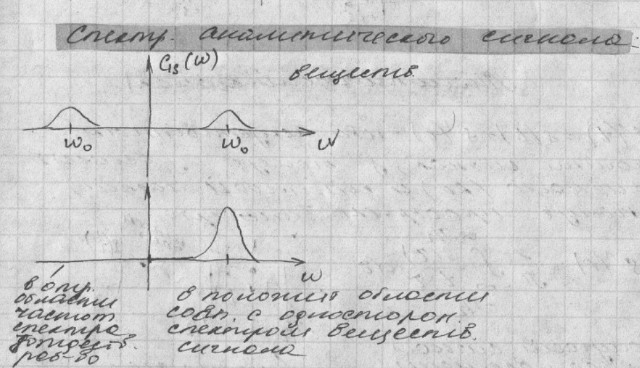
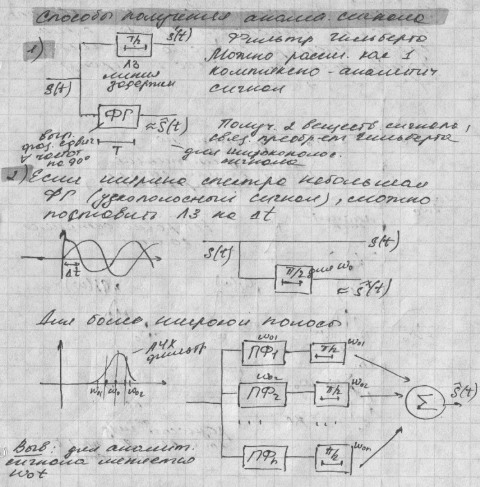
9.Вещественн.сигн на компл плоск

13.тригоном.ряд фурье

12.компл огибающ

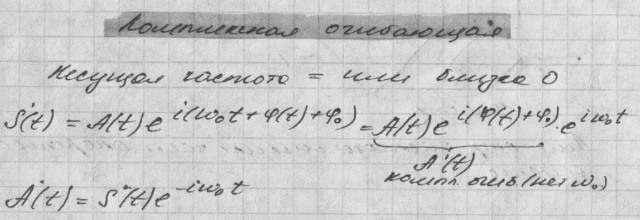
14.компл ряд фурье

15.спект непериод и период сигнл