
- •18.Линейное преобразование спектра. Функциональная схема преобразователя. Применение в устройствах радиоприема.
- •19.Амплитудная модуляция и манипуляция. Коэффициент модуляции. Спектр ам радиосигнала. Балансная и однополосная ам.
- •20.Частотная модуляция и манипуляция. Индекс модуляции. Спектр чм радиосигнала. Типы сигналов с частотной манипуляцией.
- •21.Фазовая модуляция и манипуляция. Индекс модуляции. Спектр фм радиосигнала. Типы сигналов с фазовой и амплитудно-фазовой манипуляцией.
- •27.Устойчивость замкнутых линейных цепей. Условие и критерии устойчивости.
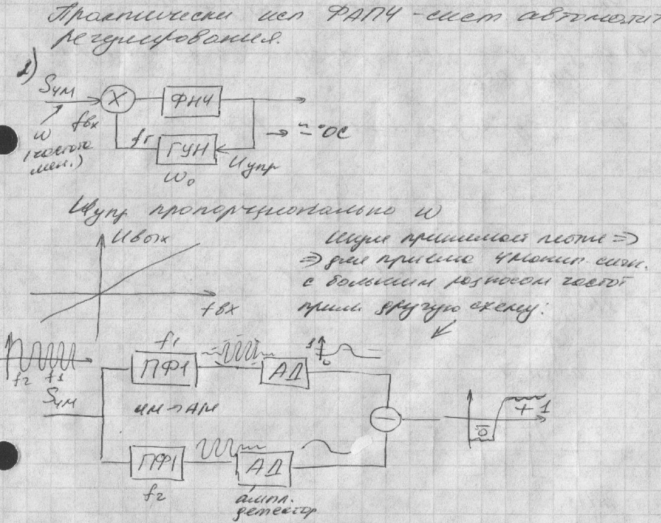
- •28.Замкнутые следящие системы. Система фазовой автоподстройки частоты. Дифференциальное уравнение системы фапч. Применение в системах передачи данных.
- •29.Анализ системы фапч без фильтра. Устойчивое и неустойчивое равновесие системы. Работа системы фапч в режиме захвата (слежения). Свойства и характеристики системы фапч.
18.Линейное преобразование спектра. Функциональная схема преобразователя. Применение в устройствах радиоприема.
![]() Если
некоторому сигналу s(t)
соответствует некоторый спектр G(w),
то производная этого сигнала на
гармоническую функция соответствует
следующий спектр: s(t)=G`(w)
s(t)*cosw0t=1/2*G`(w-w0)+1/2*G`(w-w0).
Прямое
Если
некоторому сигналу s(t)
соответствует некоторый спектр G(w),
то производная этого сигнала на
гармоническую функция соответствует
следующий спектр: s(t)=G`(w)
s(t)*cosw0t=1/2*G`(w-w0)+1/2*G`(w-w0).
Прямое
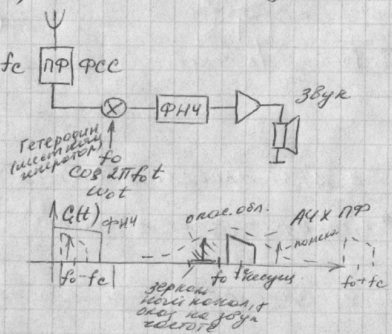 преобразование. «-» помехи попали в
полосу тоесть наложение на частоту
полезного сигнала.
преобразование. «-» помехи попали в
полосу тоесть наложение на частоту
полезного сигнала.
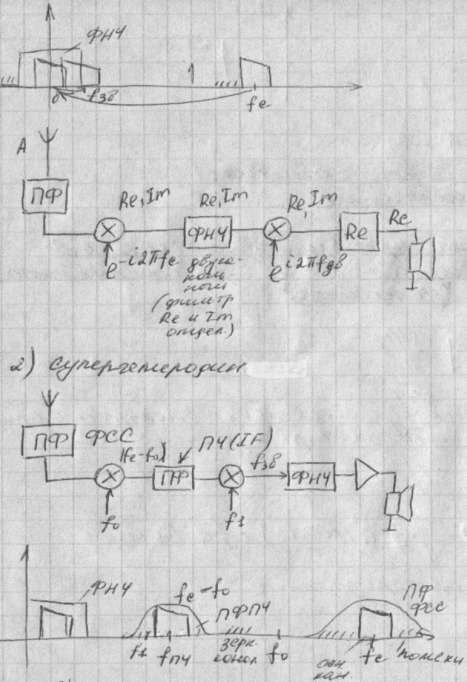
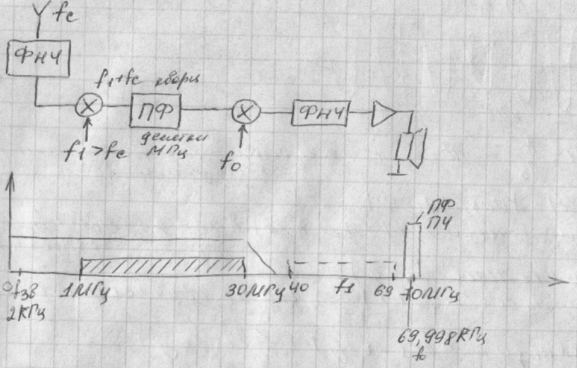
3)Супергетеродин с 2,3 преобразованием. Добавляем еще один каскад (зеркальный канал отодвигается)
4)супергетероин с приобретение частоты «вверх»
19.Амплитудная модуляция и манипуляция. Коэффициент модуляции. Спектр ам радиосигнала. Балансная и однополосная ам.
Sам(t)=A(t)cos(w0t+φ). А(t)-должно быть >0, так как если А(t)<0 то произойдет перемодуляция и искажение сигнала. Огибающая д.б. >=0 ->A(t)=x(t)+A0 (A0 > самого min значения х(t)).

![]()
М=Х/А0 М=0…1-глубина(коэфицент) модуляции. x(t)=Xcos(омега *t+ψ) огибающая А(t)=A0+xcos(омега *t+ψ)= A0(1+x/A0 *cos(омега *t+ φ)) A(t)=A0(1+Mcos(омега *t+ψ)) Sa0(t)= A0+xcos(омега *t+ψ)+ A0Mcos(омега *t+ψ)* cos(w0t+φ)= A0cos(w0t+φ)+A0M/2 *cos((w-омега)*t+ φ-ψ)+A0M/2 * A0M/2 *cos((w+омега)*t+ φ-ψ) -3 спектральных составляющих. сosx*cosy=1/2cos(x+y)+1/2cos(x-y)

Вывод:АМ колебания в случаях гармонического сигнала имеет дискретный спектр, альфа состояний из несущей и 2-х боковых частей.
Амплитудная монипуляция:

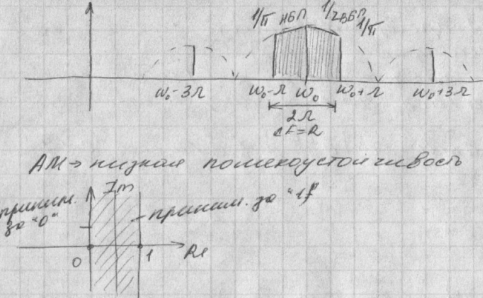
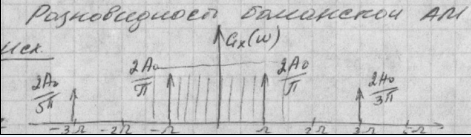
Балансная АМ (DSB)-двухполосная А0=0 (нарушить условие когда огибающая положительна).
![]()
АМ с ОБП(SSB)-в телефонии(особенно на коротких волнах)
![]()
«+» прием. для речевой радиосвязи (в основном на коротких волнах), высокая экономичность(эконом мощности), нет расширения в 2раза, на передачу мощность затрачивается только когда говорят-> эффект использования спектральной полосы. Som=A0/2*(x(t)cosw0t+-x`(t)sinw0t).
20.Частотная модуляция и манипуляция. Индекс модуляции. Спектр чм радиосигнала. Типы сигналов с частотной манипуляцией.
У спектральной компоненты другие амплитуды и фазы Y0(B)=sincB* π/2 Yx(B)=(2BsinB* π/2)/B2-K2
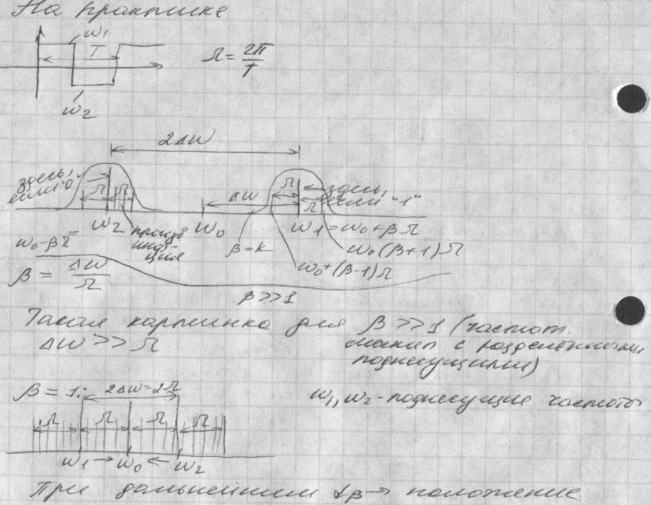
Вывод: при В>>1 дивиация частоты>>частоты омега->спектр по 2 части частотноразмещенный ЧМ сигнал. При низком индексе модуляции- спекты нач. сближаться В=1-сблизи, при В<1-пересекаются. Сущ предел сближения(В<<1).
21.Фазовая модуляция и манипуляция. Индекс модуляции. Спектр фм радиосигнала. Типы сигналов с фазовой и амплитудно-фазовой манипуляцией.
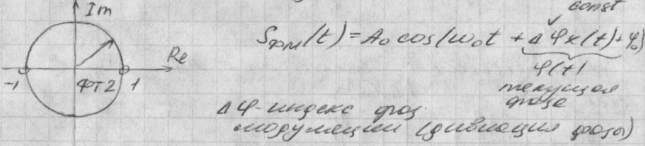
а)х(t)=cos(омега *t+ψ) S(t)=A0cos(w0t+∆φsin(омега *t+ π /2)). Спектр состав. Фазомодулированного сигнала совпадает с ЧМ сигнала. Чм,ФМ-угловые виды модуляции. б)фазовая манипуляция(фаз. телеграфия) РМ,PSK ФТ2-двухпозиционная ФГ

Спектр сдвигаем в право->А спектр мод сигнала.
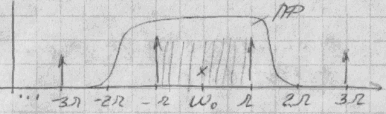
Вывод:1)спекрт 2-х позиц. ФМ-сигнала(ФМ2) явл дискретным и сост из подавления несущей. Спектры сост-щие на частотах к=0,2,4 по давляют спектр сост-щий сдвиг на 2 π
2)Отсутствие несущей приводит к усложнению демодуляторов.

22.Определение минимальной достаточной полосы частотного спектра сигналов с амплитудной, частотной и фазовой манипуляцией.
23.Линейные цепи и их звенья. Передаточная функция. Временные и частотные характеристики звеньев, связь между ними.






![]()
24.Анализ линейных цепей. Точные методы анализа линейных цепей по их частотным и временным характеристикам.

Методы анализа делятся на точечные и приближенные. Точечные делятся на решение ДУ и на спектральный метод и операторный метод. По временным характеристикам (метод интегралов наложения).


25.Типовые линейные звенья. Соединение звеньев.
1)Позиционные звенья: -безинерционное звено(его реакция не зависит от времени) К(р)=к-коэфицент усиления(ослабление сигнала) (усиливает или ослабляет сигнал), к(w)=K.
26.Оптимальная линейная фильтрация сигнала. Согласованный фильтр, его импульсная характеристика.
Оптимальным фильтром называется фильтр, который решает задачу отделения полезного сигнала от шума наилучшим образом с точки зрения выбранного критерия оптимальности
1 критерий – обнаружение сигнала (в радиолокации)
2 критерий – воспроизведение сигнала (полосовой фильтр АЧХ = 1)
Согласованная фильтрация
Согласованный фильтр – оптимальный фильтр для первого критерия – имеющий АЧХ:
![]() и
ФЧХ:
и
ФЧХ:
![]() -
фильтр, согласованный с этим сигналом
-
фильтр, согласованный с этим сигналом
![]() - фазовый спектр
- фазовый спектр
![]() - момент t,
в котором будет воспроизводится
обнаружение сигнала
- момент t,
в котором будет воспроизводится
обнаружение сигнала
Импульсная характеристика согласованного фильтра – зеркальная копия входного сигнала, сдвинутого вдоль оси t на величину t0.
g(t)
=
![]()
