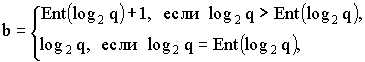4)Определение количества информации, представленной с помощью знаковых систем. Мера Хартли

  Введем понятия глубины сообщения и длины сообщения.  

  Глубина сообщения q - количество различных элементов (символов, знаков), принятых для представления сообщений. В каждый момент времени реализуется только один какой-либо элемент.

Например, если сообщение представляется символами - буквами русского алфавита, то q = 32 (для простоты буква ё во внимание не принимается), английского - q = 26. Если сообщение - десятичные числа, то q = 10 (десятичные цифры - элементы - 0, 1, 2, 3, 4, 5, 6, 7, 8, 9).   Длина сообщения n - количество позиций, необходимых и достаточных для представления сообщений заданной величины.

Если символы сообщения - цифры, то сами сообщения - числа и их последовательности.

Далее в настоящей книге понятие глубины сообщения будет трансформировано в понятиеоснования системы счисления.   При заданных глубине и длине сообщения количество всех возможных сообщений (N), которое можно представить: 

Например, всего трехбуквенных русских слов N = 32³ = 32768. Заметим, что в это количество включены и "совершенно невозможные" слова, например "ааа" или "ььы", но, подчеркнем, что при описываемом подходе смысл (семантика) сообщения не рассматривается.

Другой пример. Трехзначных десятичных чисел всего N = 10³ = 1000.  

  Величина N не удобна для оценки информационной емкости. Определим логарифмическую меру, позволяющую вычислять количество информации в битах. Такую информационную емкость (I) называют мерой Хартли: 

Для трехбуквенных русских слов I = 3 · log₂ 32 = 15.  

  Значение b = log₂ q - количество двоичных разрядов для кодирования (представления) одного элемента. Это значение не может быть дробным, поэтому более точно: 

где Ent(...) означает целую часть числа.  

  Итак, 1 бит информации соответствует одному элементарному событию, которое может произойти или не произойти. Такая мера количества информации удобна тем, что она позволяет оперировать мерой как числом. Количество информации при этом эквивалентно количеству двоичных символов 0 или 1.  

  При наличии нескольких источников информации общее количество информации равно

Здесь I _i - количество информации от источника i. Всего источников - k.  

  Логарифмическая мера информации позволяет измерить количество информации и используется на практике.

В качестве примера рассмотрим следующую задачу.  

  Необходимо определить, какое количество информации в битах содержит книга, написанная на русском языке, содержащая 200 страниц (каждая страница содержит приблизительно 2000 символов).

Для решения воспользуемся мерой Хартли

I = n · log₂ q = 200 · 2000 · log₂ 32 = 2000000 бит.

Здесь n - длина сообщения в знаках:

n = 200 страниц · 2000 знаков/страница = 400000 знаков.

Итак, книга содержит около 2-х мегабит (Мбит) информации.