Вопрос 51. Вычисление несобственных интегралов с помощью вычетов.

Для вычисления несобственных интегралов с применением теории вычетов используют следующие две леммы:

1. Пусть функция   голоморфна в верхней полуплоскости   и на вещественной оси за исключением конечного числа   полюсов, не лежащих на вещественной оси и  . Тогда

.

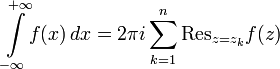2. Пусть функция   голоморфна в верхней полуплоскости   и на вещественной оси за исключением конечного числа   полюсов, не лежащих на вещественной оси,   и  . Тогда

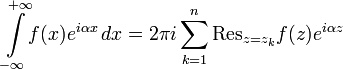
При этом интегралы в левых частях равенств не обязаны существовать и поэтому понимаются только лишь в смысле главного значения (по Коши).

Вопрос 52. Лемма Жордана. Вычисление интегралов от тригонометрических функций

Лемма Жордана. Пусть функция - аналитическая в полуплоскости ( ) за исключением конечного числа особых точек. Пусть где . Тогда выполнено

.

Замечание. Применяя лемму Жордана к функции , можно сформулировать лемму Жордана для полуплоскости .

Пусть функция - аналитическая в полуплоскости ( ) за исключением конечного числа особых точек. Пусть где . Тогда выполнено

.

Пример (стр. 214 задачника А.В. Ефимова, Б.П. Демидовича, ч.2 1986).

Вычислить интегралы , . Эти интегралы являются мнимой и действительной частями интеграла , к которому применима лемма Жордана. Подынтегральная функция, как функция комплексной переменной, имеет в в верхней полуплоскости один полюс . Вычисляя вычет и применяя общую теорему о вычетах, получим

= = +i .

Поэтому = , = .