Вопрос 41. Формулы интегрирования для неаналитических и аналитических функций

Пусть функция f (z) – определена и непрерывна в области G, а G – кусочно-гладкая кривая, лежащая в области G; z=x+iy, f(z)=u+iv, где u=u(x,y), v=v(x,y) – действительные функции переменных x и y. Вычисление интеграла от функции w=f(z) сводится к вычислению криволинейных интегралов второго рода

Если кривая задана параметрическими уравнениями x=x(t), y=y(t), а начальная и конечная точки дуги соответствуют значениям t=a, t=b, то

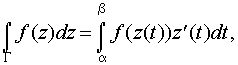
где z(t)=x(t)+iy(t).

Теорема: Если f(z) является аналитической функцией в некоторой односвязной области G, ограниченной кусочно-гладкой кривой Г, и на самой кривой, то

, (теорема Коши), и для любой внутренней точки z_0ОG имеем  (интегральная формула Коши).

Кроме того, справедлива формула

Из теоремы Коши следует, что если w=f(z) – аналитическая функция в односвязной области G, то интеграл   не зависит от пути интегрирования В этом случае для вычисления интеграла применяется формула Ньютона-Лейбница:

 где F(z) – какая-либо первообразная функции f(z), т. е. F'(z)=f(z).

Для нахождения первообразной аналитической функции f(z) применяют те же табличные формулы и приемы интегрирования, что и при нахождении неопределенных интегралов для функций действительного переменного. 

здесь кривые g₀, g₁,... g_n обходятся в “положительном” направлении, т. е. против часовой стрелки.

Если теперь z0ОD, то выполняется также и интегральная формула Коши:

Вопрос 42. Интеграл вида …

Интеграл   (n = 0, ±1, ±2, ±3, …). Возможные случаи: 1. Точка z₀ лежит вне контура L. В этом случае подынтегральная функция аналитична в замкнутой области, ограниченной контуром, и интеграл равен нулю при любых целых n.          2. n ≥ 0. И здесь подынтегральная функция аналитична, и интеграл равен нулю.          3. n = - 1, и точка z₀ лежит в области, ограниченной контуром L. Сведём интеграл по контуру L к более простому интегралу по окружности L_ρс центром в точке z₀ радиуса ρ столь малого, что окружность L_ρ лежит внутри L. В двухсвязной области, расположенной между L и L_ρ, функция   аналитична, поэтому (следствие из Теоремы Коши для многосвязной области)  . Правый интеграл вычислим напрямую. Как и при вычислении любого криволинейного интеграла, мы должны параметризовать кривую. Если z₀ = x₀ + iy₀, то параметрические уравнения окружности радиуса ρ с центром в точке (x₀, y₀) имеют вид   Можно воспользоваться этими уравнениями, однако проще собрать их в комплексное число: z = x + iy = (x₀ + ρ cosφ) + iy(y₀ + ρ sinφ) = (x₀ + iy₀) + ρ( cosφ + i sinφ) = z₀ + ρ e^iφ (таково параметрическое уравнение окружности на комплексной плоскости С), тогда dz = ρ i e^iφ, и 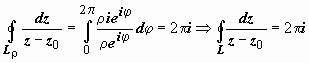 .          4. n = -2, -3, -4, … . Выкладки в этом случае такие же, как и в предыдущем.  вследствие периодичности первообразной. 

Вопрос 43. Интегральная формула Коши

Пусть f(z)  C  ( ). Выразим f(z₀)  z₀   g через значения f(z) на  . Рассмотрим  j(z)=  C  ( /z₀). Поэтому, если в области g взять такой замкнутый контур g , чтобы точка z₀ попала внутрь ограниченной им области, то j (z) будет аналитической вдвухсвязной области g^*, заключенной между   и g . По теореме Коши для многосвязной области. интеграл от функции j(z) по кривой  +g равен 0:  .Т.к.  , то  . Поскольку интеграл, стоящий слева не зависит от выбора контура, то эти свойством обладает и интеграл, стоящий справа. Удобно в качестве контура интегрирования выбрать окружность g_r с центром в точке z₀ и радиуса r . Положив на g _r x = z₀+r e^ij,  dx = ir e^ijdj , получим  f(x )dj =i [f(x )-f(z₀)]dj + i f(z₀)dj =I+2p f(z₀).  Оценим I. | I | 2p |f(x )-f(z₀)|. Устремим r  0 при этом. x (r )  z₀.Т.к. f(z)- аналитическая, а следовательно непрерывная в g, то для "e >0 $ d (e )>0 такое, что  |f(x )-f(z₀)|< e, как только |x (r )-z₀|<d. А это значит, что при r  0   I 0. Поскольку левая часть и второе слагаемое правой части не зависят от r , то переходя к пределу в обоих частях, получиминтегральную формулу Коши: f(z₀)=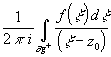 .