
- •Вопрос 35. Дифференцирование функций комплексной переменной. Условие Коши-Римана.
- •Вопрос 36. Понятие аналитической функции. Ее свойства. Условие гармоничности
- •Вопрос 37. Восстановление аналитической функции комплексной переменной по ее действительной (мнимой) части. План решения
- •1. Находим частные производные заданной функции u(X,y) (или V(X,y)).
- •2. Используя условия Коши — Римана
- •4. Находим значение постоянной c, используя значение . Записываем ответ.
- •Вопрос 38. Интеграл от функции комплексной переменной. Его свойства. Вычисление
- •Вопрос 39. Теорема Коши для односвязной области
- •Вопрос 40. Теорема Коши для многосвязной области
- •Вопрос 41. Формулы интегрирования для неаналитических и аналитических функций
- •Вопрос 42. Интеграл вида …
- •Вопрос 43. Интегральная формула Коши
- •Вопрос 44. Интегральная формула Коши для производных
- •Вопрос 45. Ряд Тейлора для функций комплексного переменного
- •Вопрос 46. Ряд Лорана
- •Вопрос 47. Нули и особые точки функции. Классификация особых точек
- •Вопрос 48. Понятие вычета.
- •Вопрос 49. Нахождение вычетов для различных типов особых точек
- •Вопрос 50. Основная теорема о вычетах
- •Вопрос 51. Вычисление несобственных интегралов с помощью вычетов.
- •Вопрос 52. Лемма Жордана. Вычисление интегралов от тригонометрических функций
Вопрос 35. Дифференцирование функций комплексной переменной. Условие Коши-Римана.
Пусть функция w=f (z) определена в некоторой области G комплексной плоскости. Пусть точки z и z+Dz принадлежат области G. Положим Dw=f (z+Dz)–f (z), Dz = Dx+iDy.
Функция
w=f (z) называется дифференцируемой
в точке zОG, если
существует предел
![]() Этот
предел называют производной
функции f (z) и
обозначают
через f¢ (z )
(или
Этот
предел называют производной
функции f (z) и
обозначают
через f¢ (z )
(или ![]() ).
).
Итак,
![]()
Пусть z=x+iy, w=f (z)=u(x,y)+iv(x,y), тогда в каждой точке дифференцируемости функции f (z) выполняются соотношения:
![]()
Эти соотношения принято называть условиями Коши-Римана (или уравнениями Коши-Римана). Когда в некоторой точке (x,y) выполняются условия Коши-Римана и, кроме того, функции u(x,y) и v(x,y) дифференцируемы как функции действительных переменных, то функция f (z)=u+iv дифференцируема в точке z=x+iy как функция комплексного переменного z.
Вопрос 36. Понятие аналитической функции. Ее свойства. Условие гармоничности
Функция
f(z)![]() C(g),
дифференцируемая (моногенная) во всех
точках z
g,
производная которой f ' (z)
C(g)
называется аналитической
функцией в
области g.
C(g),
дифференцируемая (моногенная) во всех
точках z
g,
производная которой f ' (z)
C(g)
называется аналитической
функцией в
области g.
Обозначение:
f(z)
C![]() (g).
Понятие
аналитичности функции определяет
глобальное поведение f(z) в области g.
(g).
Понятие
аналитичности функции определяет
глобальное поведение f(z) в области g.
Свойства аналитических функций.
1) Если
f(z)
C
(g) (аналитическая
в g),
то f(z)
C(g)
(непрерывна в g).
2)
Сумма и произведение аналитических
функций есть аналитическая функция.
Частное аналитических функций есть
аналитическая функция всюду, где
знаменатель отличен от нуля.
3)
Если w=f(z)
C
(g)
- аналитическая функция комплексной
переменной z, причем
в области ее значений G на
плоскости w определена
аналитическая функция
x=j (w)
C
(G),
то функция F(z)= j [f(z)]
C
(g)
-аналитическая функция комплексной
переменной z в
области g.
4) Пусть w=f(z)=u(x,y)+iv(x,y)
C
(g)
и f
'(z0)![]() 0,
z0
g. Тогда
в окрестности точки w0=f(z0) определена
обратная аналитическая
функция z=j (w)
C
(|w-w0|<e ) отображающая
эту окрестность на окрестность точки z0,
причем j'(w0)=1/
f '(z0).
0,
z0
g. Тогда
в окрестности точки w0=f(z0) определена
обратная аналитическая
функция z=j (w)
C
(|w-w0|<e ) отображающая
эту окрестность на окрестность точки z0,
причем j'(w0)=1/
f '(z0).
5) Пусть в односвязной области g плоскости (x,y) задана функция u(x,y), являющаяся действительной частью аналитической функции f(z). Тогда мнимая часть этой функции определяется с точностью до аддитивной постоянной.
Условие
Гармоничности:
Дифференцируя первое соотношение
Коши-Римана ![]() по
переменной х,
второе соотношение
по
переменной х,
второе соотношение ![]() по
переменной у,
получим
по
переменной у,
получим 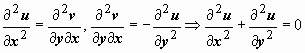 ,
т.е. Δu =
0 (Δ - оператор Лапласа), т.е. u(x, y)
- гармоническая функция. Дифференцируя
первое соотношение Коши-Римана по
переменной у,
второе соотношение по переменной х,
получим
,
т.е. Δu =
0 (Δ - оператор Лапласа), т.е. u(x, y)
- гармоническая функция. Дифференцируя
первое соотношение Коши-Римана по
переменной у,
второе соотношение по переменной х,
получим 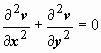 ,
т.е. Δv =
0, т.е. v(x, y)
- тоже гармоническая функция. Пара
гармонических функций, связанных
соотношениями Коши-Римана,
называется сопряжёнными
функциями.
,
т.е. Δv =
0, т.е. v(x, y)
- тоже гармоническая функция. Пара
гармонических функций, связанных
соотношениями Коши-Римана,
называется сопряжёнными
функциями.
Вопрос 37. Восстановление аналитической функции комплексной переменной по ее действительной (мнимой) части. План решения
1. Находим частные производные заданной функции u(X,y) (или V(X,y)).
2. Используя условия Коши — Римана
находим v(x,y) (или u(x,y)) с точностью до произвольной постоянной C.
3. Записываем искомую функцию f(z) = u(x,y)+iv(x,y)+C и преобразуем полученное выражение к функции переменной z, например, заменяя x и y их выражениями через переменную z:
