27. Кручение стержня прямоугольного поперечного сечения (закон распределения напряжений по сечению, зависимости для определения напряжений и перемещений).

При кручении прямоугольных стержней гипотеза плоских сечений не выполняется, так как сечения искривляются - депланируют. Задача о кручении прямоугольных стержней решается в теории упругости.

Готовые формулы

h >b

Рис. 8.5 Эпюра касательных напряжений для некруглых стержней

В углах и центре тяжести 0

где Wk = a×b2×h  - момент сопротивления при кручении

Ik = b×b3×h   - 

a, b, g -коэффициенты, зависят от соотношения 

Некоторые значения коэффициентов a, b, g.

	1	1,5	1,75	2	2,5	3	10
a	0,208	0,231	0,239	0,246	0,256	0,267	0,313
b	0,141	0,196	0,214	0,229	0,249	0,263	0,313
g	1	0,869	0,82	0,795	0,766	0,753	0,742

Абсолютный угол закручивания вала, состоящего из n участков  - j.

                            

                              

29. Понятия о стесненном и свободном кручении.

Стесненное кручение

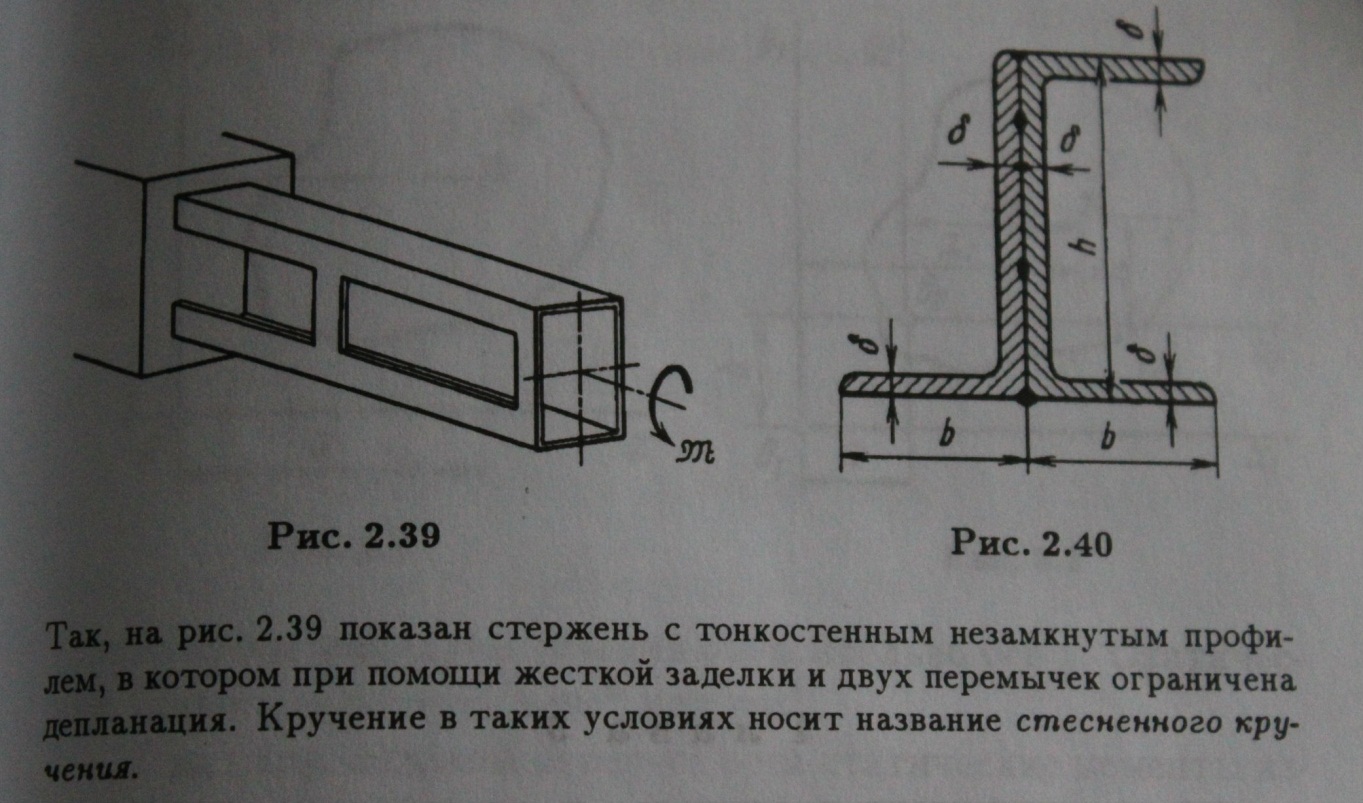
Свободное кручение

В стержнях некруглого сечения при кручении сечения не остаются плоскими, а искривляются (депланируют).

Если для такой депланации нет никаких препятствий, то в поперечных сечениях нормальных напряжений не возникает. Такое кручение называется чистым или свободным.

Свободное кручение возможно лишь при условии, что сечение стержня и крутящий момент постоянны, а концы стержня не заделаны.

30. Потенциальная энергия деформации и работа внешних нагрузок при кручении.

При кручении внешние моменты, приложенные к валу, совершают работу вследствие поворота сечений, к которым они приложены. Эта работа расходуется на создание запаса потенциальной энергии деформации, численно равной работе внутренних сил. В пределах упругих деформаций согласно закону Гука угол закручивания растет пропорционально крутящему моменту. Поэтому зависимость крутяще го момента от угла закручивания   представляет собой прямую ОА, изображенную на рисунке 11.3. Пусть угол   соответствует промежуточному значению М. Увеличим момент Рисунок 11.3 на бесконечно малую величину dM. Тогда угол получит приращение d.  Произведенная работа равна площади заштрихованной трапеции и определится соотношением  (11.10) Полная работа деформации при возрастании крутящего момента от 0 до М_кр, равная накопленной потенциальной энергии, представится площадью треугольника  и будет равна  (11.11) Подставим в формулу (11.11) значение угла закручивания ; (11.12) Получено выражение потенциальной энергии при кручении где G – модуль сдвига; – полярный момент инерции сечения;  – длина вала. Потенциальная энергия может быть выражена и через деформацию, если в формулу (11.12) подставить зависимость крутящего момента от угла закручивания. Поскольку  , то  . Таким образом, потенциальная энергия равна ;  . (11.13)