3.2 Вычисление пределов

Вычисления пределов в MathCAD при решении задач из курса высшей математики должны использоваться для проверки вычислений вручную!

Других способов проверки вычисления пределов в курсе высшей математики обычно не дается. А будущий инженер должен быть приучен к проверке всех результатов вычислений!

При вычислении пределов в MathCAD шаблон берётся с панельки Calculus, знак символьного вывода вводится нажатием клавиш Ctrl + . (точка) в латинском регистре. Знак = для числового вывода при вычислении пределов использовать нельзя!

а)

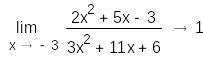
б)

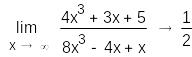
в)

г)

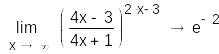
3.3 Вычисление производных

А) Вычислим производную функции f(x)

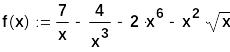
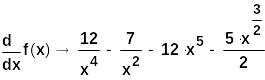
Б)

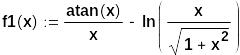
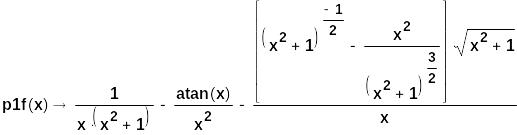
пытаемся упростить производную через символьную операцию simplify:

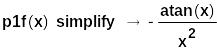
В) Любую неявно заданную функцию y(x) можно записать в виде равенства:

где

Для отыскания 1-й производной имеется известная формула:

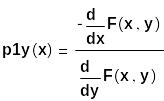
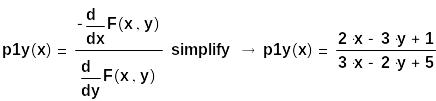
Это частная производная по .

При её отыскании считается постоянной

Это частная производная по .

При её отыскании считается постоянной

3.4 Задание 3 (4 точки в пространстве + пирамида)

Задание 3 в общем виде:

Даны 4 точки:

А1(х1,у1,z1), А2(х2,у2,z2), А3(х3,у3,z3), А4(х4,у4,z4)

Найти: 1. Объём пирамиды А1_ А2_ А3_ А4

2. Угол между прямыми A1_A2 и А1_А4 (в градусах)

3. Уравнение плоскости А1 ; А2; А3

4. Уравнение прямой А4_М, перпендикулярной к плоскости А1 ; А2; А3

Задаём исходные данные

Координаты точки А1

Координаты точки А2

Координаты точки А3

Координаты точки А4

Вычисляем координаты 3-х векторов, на которых строится пирамида:

Вектор с началом в точке А1 и

с концом в точке А2

Вектор с началом в точке А1 и

с концом в точке А3

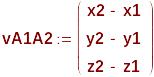
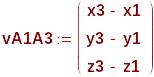
Вектор с началом в точке А1 и

с концом в точке А2

Вектор с началом в точке А1 и

с концом в точке А3

Находим матрицу и её определитель, равный смешанному произведению:

Находим объём пирамиды:

2. Угол между прямыми A1_A2 и А1_А4 (в градусах)

Находим косинус угла между двумя векторами:

Находим угол между двумя векторами в градусах:

3. Уравнение плоскости, А1 ; А2; А3:

Более подробно

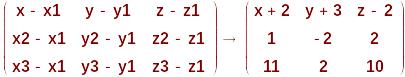
4. Уравнение прямой А4_М, перпендикулярной к плоскости А1 ; А2; А3

Нормальный вектор n этой плоскости имеет координаты:

Уравнение прямой А4_М, c направляющим вектором n: в общем виде:

А4_М

Выведем координаты точки А4:

Подставим числовые данные и получим ответ: