3. Решение задач по курсу высшей математики (для проверки «ручных» вычислений)

3.1 Решение слау 3-го порядка тремя способами

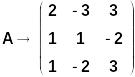
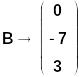
3 метода решения СЛАУ проиллюстрируем на примере СЛАУ 3-го порядка (вариант 18) вида:

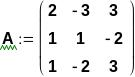
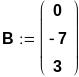
Определитель матрицы не равен 0, значит, СЛАУ имеет единственное решение.

Вычислим символьно обратную матрицу :

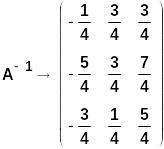
1. Решение СЛАУ через обратную матрицу:

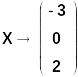
Проверка:

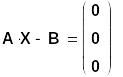
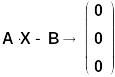
Решение СЛАУ через обратную матрицу получено с нулевой погрешностью!

2. Решение СЛАУ методом Гаусса.

Для метода Гаусса нужно создать расширенную матрицу, которая образуется путем добавления к матрице А столбца свободных членов В. Делается это с помощью функции augment:

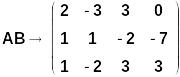
Начальный индекс массивов (системная переменная с именем ORIGIN) устанавливается в 1. Это делается для того, чтобы нумерация столбцов матриц была естественной: 1, 2, 3 ..

Используя операцию транспонирования (значок на панельке Matrix) , и операцию выделения столбца с соответствующим номером (значок на панельке Matrix) сформируем 3 отдельные строки матрицы АВ:

Делим R1 - первую строку расширенной матрицы АВ на 1-й элемент этой строки.

Преобразованную строку снова обозначим через R1;

Умножаем обновленную R1 на 1-й элемент R2

и вычитаем из R2:

Умножаем обновленную R1 на 1-й элемент R3

и вычитаем из R3:

Формируем новую расширенную матрицу с именем АВ1 при помощи функции stack:

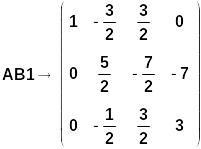
Сформируем 2-ю и 3-ю строки матрицы АВ1:

Делим R2 - на 2-й элемент этой строки.

Преобразованную строку снова обозначим через R2:

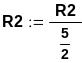
Умножаем обновленную R2 на 2-й элемент R3и вычитаем из R3:

Формируем новую расширенную матрицу с именем АВ1 при помощи функции stack:

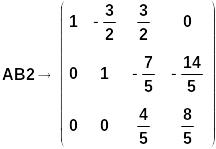
Делим R3 - на 3-й элемент этой строки. Преобразованную строку снова обозначим через R3:

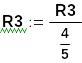
Формируем новую расширенную матрицу с именем АВ3 при помощи функции stack:

Прямой ход метода Гаусса успешно завершён! Сразу можно сказать, чему равно значение неизвестной х3!

Обратный ход аналогичен прямому, только процесс преобразования строк расширенной матрицы идет «снизу вверх»:

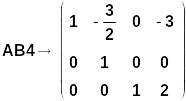
Завершающий шаг обратного хода:

Окончательный вид преобразованной расширенной матрицы:

Эта расширенная матрица эквивалентна СЛАУ:

Поэтому 4-й столбец матрицы АВ5 дает нам решение нашей СЛАУ!

Ответ:

3. Решение СЛАУ - по методу Крамера ("через определители").

Обычно этот метод используется для решения систем не выше 3 - го порядка, заданных в матрично-векторной форме.

Основные достоинства правила Крамера - возможность символьного решения и простота при решении СЛАУ "вручную".

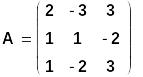
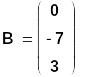
При выполнении оператора 1-й столбец матрицы становится равным вектору правой части СЛАУ.

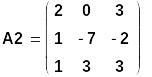
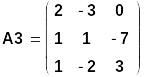
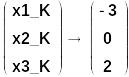
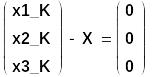
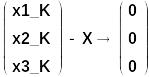
Вывод.

Все 3 способа в данном случае дали одно и то же решение. В других задачах эти решения могут незначительно разниться.