2. Решение слау 3-го порядка тремя способами

Используя как Образец файл с именем

решение СЛАУ3 тремя способами.xmcd,

И подставляя свои исходные данные получим решение задачи в следующем виде.

На основе вставленного объекта, запишем СЛАУ 3- го порядка (3 уравнения с 3-мя неизвестными) в виде:

С помощью операторов присваивания зададим для нашей СЛАУ матрицу А коэффициентов при неизвестных и вектор В правых частей:

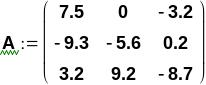
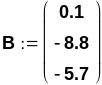
Обозначим

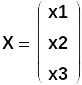
Выведем значения матричной переменной А и векторной переменной В

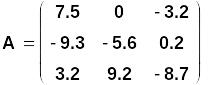
Перепишем нашу СЛАУ в развернутой матрично - векторной форме:

Используем теперь наши обозначения (А - матрица, В - вектор):

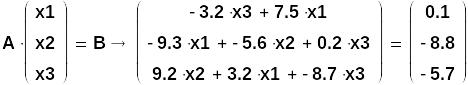
Итак, мы пришли к выводу, что наша СЛАУ, записанная вначале в обычной (скалярной) форме (1), может быть переписана в матрично-векторной форме:

Важнейшей характеристикой квадратной матрицы A является её определитель. Он вычисляется в MathCAD с помощью знака , взятого с панельки Matrix. Если определитель квадратной матрицы А отличен от 0, то эта матрица называется невырожденной и имеет обратную матрицу А^-1.Тогда СЛАУ имеет единственное решение, которое может быть найдено любым из известных способов, например, по формуле:

Вычислим определитель матрицы А:

Определитель матрицы А отличен от 0. Значит, наша СЛАУ имеет единственное решение.Это решение можно найти через обратную матрицу по формуле:

Обратная матрица легко вычисляется в MathCAD.

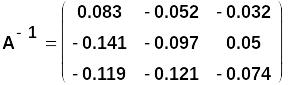
Основное свойство обратной матрицы - это равенства вида

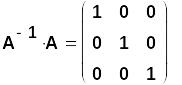
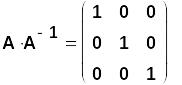
Решим теперь нашу СЛАУ тремя способами с проверкой точности получаемых решений.

1-й способ решения СЛАУ - через обратную матрицу. Имя вектора решения здесь Х, то есть, исходная СЛАУ имеет вид

Решение получается с помощью оператора присваивания:

Вычислим вектор невязки приближённого решения Х, подставляя это решение в исходную систему и вычисляя разность между левой и правой частью:

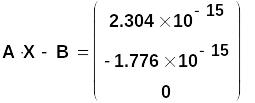
Невязка ничтожно мала. Поэтому можно считать, что вектор Х даёт нам решение с очень высокой точностью. Примем, что X - " точное" решение СЛАУ. Используя символьную операцию получим приближенное решение с Х_5 с 5-ю значащими цифрами:

Погрешность приближённого решения X_5:

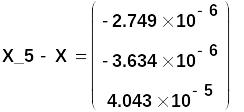
Обычно в окончательном виде у полученного решения оставляют сравнительно небольшое количество значащих цифр. Так, MathCAD "по умолчанию" выдаёт числовой результат с 3-мя цифрами после десятичной точки. В этом случае приближённое решение записывается проcто, но оно будет менее точным, и его невязка будет уже другой:

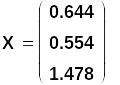
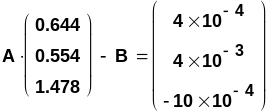
Если полученное решение используется и в дальнейшем, его лучше сохранять без потери точности, с максимальным числом значащих цифр, не допуская округлений. И только на заключительном этапе можно оставить нужное число значащих цифр. В MathCAD это делается просто и естественно, с использованием соответствующих обозначений.

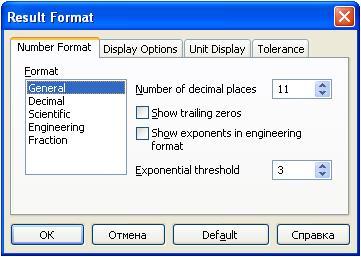
Для получения вектора решения с другим числом значащих цифр, достаточно дважды щелкнуть по одному из элементов числового вектора и в появившемся диалоговом окне установить нужно число цифр после десятичной точки, например, 11 :

2-й способ решения СЛАУ - через специальную функцию lsolve.

Полученное решение обозначим через Xs:

Используя числовой и символьный вывод, проверим, насколько вектор Xs отличается от ранее найденного Х:

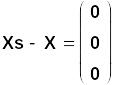
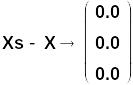
Как и следовало ожидать, решения совпали.

3-й способ решения СЛАУ - через вычислительный блок Given/Find

Так как наша система линейна, задаем произвольные (нулевые) начальные приближения к искомым величинам х1, х2, х3:

После служебного слова Given (Дано) скопируем СЛАУ, сформированную ранее (это делается через обычное копирование):

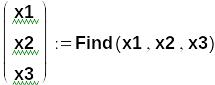
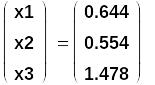
Через функцию Find мы получили решение СЛАУ, записанной в обычной форме в виде вектора

Сравним это решение с вектором Х:

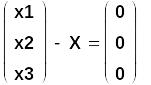
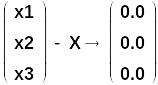
Как и следовало ожидать, эти решения совпали!

Итак, все 3 способа в нашем случае дали одинаковый результат. Отметим, однако, что результат, полученный через блок Given/Find, часто дает менее точный результат, чем первые два. Кроме того, через блок Given/Find можно получить одно решение, когда СЛАУ вырожденна (её определитель равен 0) и имеет бесконечное множество решений.