Иванов Петр Сидорович гр. П-777 ФЗО Шифр 1077707 КР№1 2012 год

Вариант 18

Оглавление.

Введение 2

1. Исследование f(x) на [a; b] 2

2. Решение СЛАУ 3-го порядка тремя способами 6

3. Решение задач по курсу высшей математики (для проверки «ручных» вычислений) 12

3.1 Решение СЛАУ 3-го порядка тремя способами 12

3.2 Вычисление пределов 20

3.3 Вычисление производных 21

3.4 Задание 3 (4 точки в пространстве + пирамида) 23

Заключение. 26

Введение

КР№1 выполнена на основе Образцов, разработанных доцентом кафедры информатики и прикладной математики Брестского государственного технического университета (БрГТУ) В.Г. Афониным.

В большинстве случаев Образец для решения конкретной задачи в СКМ MathCAD представляет собой хорошо документированный Вычислительно-Графический Документ (ВГД).

Как правило, работа с такими ВГД предельно проста. Достаточно просто подставить в ВГД свои исходные данные и внести элементарные изменения и дополнения. При этом качество такого решения получается достаточно высоким (с проверкой, с нужными пояснениями и т.д.).

Кроме того, широко использовалась методическая разработка доцента В.Г. Афонина «Краткие сведения (Памятка) по работе и решению задач в MathCAD».

В частности, оформление данного отчета проводилось на базе раздела «6. О копировании различных областей из MathCAD в Word» этой методической разработки. Использовались и другие учебно-методические материалы.

1. Исследование f(X) на [a; b]

Задание. Используя Образец исследования f(x)

для функции f (x) своего варианта решить следующие задачи:

найти 1-й корень, 1-й локальный максимум и 1-й локальный минимум

функции f (x) на отрезке [a; b]. Номер варианта, где заданы значения a, b, k -

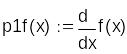
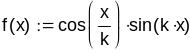
Для отыскания корня можно использовать встроенную функцию root в 2-х вариантах.

1-й вариант - На основе графика задаётся интервал, содержащий один искомый корень

2-й вариант - На основе графика задаётся начальное приближение к искомому корню:

Функцию root можно использовать и для отыскания точек локальных экстремумов, где обращается в 0 производная функции:

Задача поиска локального минимума успешно решена!

Аналогично решается задача поиска локального максимума:

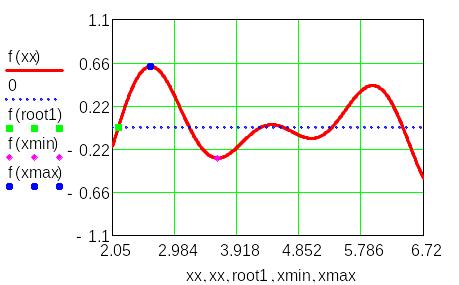
Найденные точки: корень, максимум, минимум отобразим на графике в виде отдельных точек:

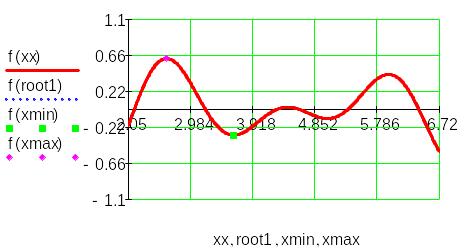
Отыскания корня уравнения f(x)=0 на базе блока Given/Find

- задаётся начальное приближение к искомому корню

Блок Given/Minimize для отыскания минимума:

задаётся начальное приближение к искомому минимуму

- задаётся интервал, содержащий искомый минимум

- Значение производной в точке локального минимума должно быть равно 0.

Блок Given/Maximize для отыскания максимума:

- задаётся начальное приближение к искомому максимуму

- задаётся интервал, содержащий искомый максимум

- Значение производной в точке локального максимума должно быть равно 0.