Бехтин, вопрос 1.

Моделирование как метод научного познания. Цели моделирования.

Методологическая основа моделирования. Все то, на что направ­лена человеческая деятельность, называется объектом (лат. objection - предмет). Выработка методологии направлена на упо­рядочение получения и обработки информации об объектах, кото­рые существуют вне нашего сознания и взаимодействуют между собой и внешней средой.

В научных исследованиях большую роль играют гипотезы, т. е. определенные предсказания, основывающиеся на небольшом коли­честве опытных данных, наблюдений, догадок. Быстрая и полная проверка выдвигаемых гипотез может быть проведена в ходе специ­ально поставленного эксперимента. При формулировании и провер­ке правильности гипотез большое значение в качестве метода сужде­ния имеет аналогия.

Аналогией называют суждение о каком-либо частном сходстве двух объектов, причем такое сходство может быть существенным и несущественным. Необходимо отметить, что понятия существен­ности и несущественности сходства или различия объектов условны и относительны. Существенность сходства (различия) зависит от уровня абстрагирования и в общем случае определяется конечной целью проводимого исследования. Современная научная гипотеза создается, как правило, по аналогии с проверенными на практике научными положениями. Таким образом, аналогия связывает гипо­тезу с экспериментом.

Гипотезы и аналогии, отражающие реальный, объективно суще­ствующий мир, должны обладать наглядностью или сводиться к удобным для исследования логическим схемам; такие логические схемы, упрощающие рассуждения и логические построения или позволяющие проводить эксперименты, уточняющие природу явле­ний, называются моделями.

Другими словами, модель (лат. modulus — мера) — это объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала.

Основные понятия системного анализа. Специалисты по проектированию и эксплуатации сложных систем имеют дело с системами управления различных уровней, обладающими общим свойством - стремлени­ем достичь некоторой цели. Эту особенность учтем в следующих определениях системы.

Система S — целенаправленное множество взаимосвязанных элементов любой природы.

Внешняя среда Е — множество существующих вне системы элементов любой природы, оказывающих влияние на систему или находящихся под ее воздей­ствием.

Понятие модели. Модель – представление объекта, системы или понятия, в некоторой форме, отличного от их реального существования.

Моделирование – во-первых, построение модели, во-вторых, изучение модели, в-третьих, анализ системы на основе данной модели.

При системном подходе к моделированию систем необходимо прежде всего четко определить цель моделирования. Применительно к вопросам моделирования цель возникает из требуемых задач моделирования, что позволяет по­дойти к выбору критерия и оценить, какие элементы войдут в со­здаваемую модель М. Поэтому необходимо иметь критерий отбора отдельных элементов в создаваемую модель.

Цели моделирования:

1) оценка – оценить действительные характеристики проектируемой или существующей системы, определить насколько система предлагаемой структуры будут соответствовать предъявляемым требованиям.

2) сравнение – произвести сравнение конкурирующих систем одного функционального назначения или сопоставить несколько вариантов построения одной и той же системы.

3) прогноз – оценить поведение системы при некотором предполагаемом сочетании рабочих условий.

4) анализ чувствительности – выявить из большого числа факторов, действующих на систему тем, которое в большей степени влияют на ее поведение и определяют ее показатели эффективности.

5) оптимизация – найти или установить такое сочетание действующих факторов и их величин, которое обеспечивает наилучшие показатели эффективности системы в целом.

1-4 задачи анализа, 5 - задача синтеза.

Бехтин, вопрос 2.

Классификация видов моделей систем.

В основу классификации положена степень абстрагирования модели от оригинала. Предварительно все модели можно подразделить на 2 группы — физические и абстрактные (математические).

Физической моделью обычно называют систему, эквивалентную или подобную оригиналу, но возможно имеющую другую физическую природу. Виды Ф.М.:

• натуральные;

• квазинатуральные;

• масштабные;

• аналоговые;

Натуральные модели — это реальные исследуемые системы (макеты, опытные образцы). Имеют полную адекватность (соответствия) с системой оригиналом, но дороги.

Квазинатуральные модели — совокупность натуральных и математических моделей. Этот вид используется тогда, когда модель части системы не может быть математической из-за сложности её описания (модель человека оператора) или когда часть системы должна быть исследована во взаимодействии с другими частями, но их ещё не существует или их включение очень дорого (вычислительные полигоны, АСУ).

Масштабная модель — это система той же физической природы, что и оригинал, но отличается от него масштабами. Методологической основой масштабного моделирования является теория подобия. При проектировании ВС масштабные модели могут использоваться для анализа вариантов компоновочных решений.

Аналоговыми моделями называют системы, имеющие физическую природу, отличающуюся от оригинала, но сходные с оригиналом процессы функционирования. Для создания аналоговой модели требуется наличие математического описания изучаемой системы. В качестве аналоговых моделей используются механические, гидравлические, пневматические и электрические системы. Аналоговое моделирование использует при исследовании средства ВТ на уровне логических элементов и электрических цепей, а так же на системном уровне, когда функционирование системы описывается, например, дифференциальными или алгебраическими уравнениями.

Математические модели. Математические модели представляют собой формализованное представление системы с помощью абстрактного языка, с помощью математических соотношений, отражающих процесс функционирования системы. Для составления математических моделей можно использовать любые математические средства — алгебраическое, дифференциальное, интегральное исчисления, теорию множеств, теорию алгоритмов и т.д. По существу вся математика создана для составления и исследования моделей объектов и процессов.

К средствам абстрактного описания систем относятся также языки химических формул, схем, чертежей, карт, диаграмм и т.п. Выбор вида модели определяется особенностями изучаемой системы и целями моделирования, т.к. исследование модели позволяет получить ответы на определённую группу вопросов. Для получения другой информации может потребоваться модель другого вида. Математические модели можно классифицировать как детерминированные и вероятностные, аналитические, численные и имитационные.

Детерминирован­ное моделирование отображает процессы, в которых предполагается отсутствие всяких случайных воздействий; стохастическое моделирование отображает вероят­ностные процессы и события. В этом случае анализируется ряд реализаций случайного процесса и оцениваются средние характе­ристики, т. е. набор однородных реализаций.

Аналитической моделью называется такое формализованное описание системы, которое позволяет получить решение уравнения в явном виде, используя известный математический аппарат.

Численная модель характеризуется зависимостью такого вида, который допускает только частные решения для конкретных начальных условий и количественных параметров моделей.

Имитационная модель — это совокупность описания системы и внешних воздействий, алгоритмов функционирования системы или правил изменения состояния системы под влиянием внешних и внутренних возмущений.

Эти алгоритмы и правила не дают возможности использования имеющихся математических методов аналитического и численного решения, но позволяют имитировать процесс функционирования системы и производить вычисления интересующих характеристик. Имитационные модели могут быть созданы для гораздо более широкого класса объектов и процессов, чем аналитические и численные. Поскольку для реализации имитационных моделей служат ВС, средствами формализованного описания ИМ служат универсальные и специальные алгоритмические языки. ИМ в наибольшей степени подходят для исследования ВС на системном уровне.

Бехтин, вопрос 3.

Подходы к исследованию систем. Важным для системного под­хода является определение структуры системы — совокупности связей между элементами системы, отражающих их взаимодейст­вие.

При структурном подходе выявляются состав выделенных эле­ментов системы S и связи между ними. Совокупность элементов и связей между ними позволяет судить о структуре системы. После­дняя в зависимости от цели исследования может быть описана на разных уровнях рассмотрения. Наиболее общее описание струк­туры — это топологическое описание, позволяющее определить в самых общих понятиях составные части системы и хорошо фор­мализуемое на базе теории графов.

Менее общим является функциональное описание, когда рас­сматриваются отдельные функции, т. е. алгоритмы поведения систе­мы, и реализуется функциональный подход, оценивающий функции, которые выполняет система, причем под функцией понимается свойство, приводящее к достижению цели.

Простой подход к изучению взаимосвязей между отдельными частями модели предусматривает рассмотрение их как отражение связей между отдельными подсистемами объекта. Такой классичес­кий подход может быть использован при создании достаточно простых моделей. Процесс синтеза модели М на основе классичес­кого (индуктивного) подхода представлен на рис. 1.1, а. Реальный объект, подлежащий моделированию, разбивается на отдель­ные подсистемы, т. е. выбираются исходные данные Д для моделирования и ставятся цели Ц, отображающие отдельные сто­роны процесса моделирования. По отдельной совокупности исход­ных данных Д ставится цель моделирования отдельной стороны функционирования системы, на базе этой цели формируется некото­рая компонента К будущей модели. Совокупность компонент объ­единяется в модель М.

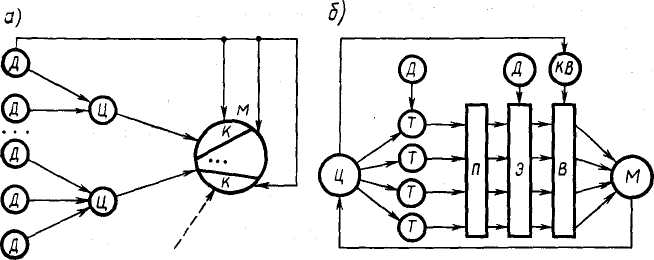
Рис. 1.1. Процесс синтеза модели на основе классического (а) и системного (б) подходов

Таким образом, разработка модели М на базе классического подхода означает суммирование отдельных компонент в единую модель, причем каждая из компонент решает свои собственные задачи и изолирована от других частей модели. Поэтому классичес­кий подход может быть использован для реализации сравнительно простых моделей, в которых возможно разделение и взаимно неза­висимое рассмотрение отдельных сторон функционирования реаль­ного объекта. Для модели сложного объекта такая разобщенность решаемых задач недопустима, так как приводит к значительным затратам ресурсов при реализации модели на базе конкретных программно-технических средств. Можно отметить две отличитель­ные стороны классического подхода: наблюдается движение от частного к общему, создаваемая модель (система) образуется путем суммирования отдельных ее компонент и не учитывается возник­новение нового системного эффекта.

Процесс синтеза модели М на базе системного подхода условно представлен на рис. 1.1, б. На основе исходных данных Д, которые известны из анализа внешней системы, тех ограничений, которые накладываются на систему сверху либо исходя из возможностей ее реализации, и на основе цели функционирования формулируются исходные требования Т к модели системы S. На базе этих требова­ний формируются ориентировочно некоторые подсистемы П, эле­менты Э и осуществляется наиболее сложный этап синтеза — вы­бор В составляющих системы, для чего используются специальные критерии выбора КВ.

Стадии разработки моделей. На базе системного подхода может быть предложена и некоторая последовательность разработки мо­делей, когда выделяют две основные стадии проектирования: мак­ропроектирование и микропроектирование.

На стадии макропроектирования на основе данных о ре­альной системе S и внешней среде Е строится модель внешней среды, выявляются ресурсы и ограничения для построения моде­ли системы, выбирается модель системы и критерии, позволяющие оценить адекватность модели М реальной системы S.

Стадия микропроектирования в значительной степени зави­сит от конкретного типа выбранной модели. В случае имитацион­ной модели необходимо обеспечить создание информационного, математического, технического и программного обеспечений систем моделирования.

Независимо от типа используемой модели М при ее построении необходимо руководствоваться рядом принципов системного под­хода:

1) пропорционально-последовательное продвижение по этапам и направлениям создания модели;

2) согласование информаци­онных, ресурсных, надежностных и других характеристик;

3) пра­вильное соотношение отдельных уровней иерархии в системе моде­лирования;

4) целостность отдельных обособленных стадий постро­ения модели.

Бехтин, вопрос 4.

Математические методы моделирования систем.

Основные этапы построения математической модели:

1. составляется описание функционирования системы в целом;

2. составляется перечень подсистем и элементов с описанием их функционирования, характеристик и начальных условий, а также взаимодействия между собой;

3. определяется перечень воздействующих на систему внешних факторов и их характеристик;

4. выбираются показатели эффективности системы, т.е. такие числовые характеристики системы, которые определяют степень соответствия системы ее назначению;

5. составляется формальная математическая модель системы;

6. составляется машинная математическая модель, пригодная для исследования системы на ЭВМ.

Требования к математической модели:

Требования определяются прежде всего ее назначением, т.е. характером поставленной задачи:

"Хорошая" модель должна быть:

1. целенаправленной;

2. простой и понятной пользователю;

3. достаточной с точки зрения возможностей решения поставленной задачи;

4. удобной в обращении и управлении;

5. надежной в смысле защиты от абсурдных ответов;

6. допускающей постепенные изменения в том смысле, что, будучи вначале простой, она при взаимодействии с пользователями может становиться более сложной.

Математическая модель, в широком смысле, это приближенное описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики. Применительно к задачам исследования качества системы математическая модель должна обеспечивать адекватное описание влияния параметров и условий функционирования на показатели ее качества. Что касается точности модели, то ее уровень должен обеспечивать достоверное сравнительное оценивание и ранжирование по уровню качества альтернативных вариантов

В основе изучения и моделирования процессов функционирования технических систем всегда лежит эксперимент - реальный или логический. Суть реального эксперимента состоит в непосредственном изучении конкретного физического объекта. В ходе логического эксперимента свойства объекта исследуются не на самом объекте, а с помощью его математической или содержательной (словесной) модели, изоморфной объекту с точки зрения изучаемых эксперименте свойств.

Подавая на вход системы различные входные процессы и измеряя процесс на ее выходе, исследователь получает возможность установить и записать математически существующую между ними связь в виде уравнения, связывающего для каждого интервала времени значения входных и выходных воздействий и потому называемого уравнением «вход-выход». Кроме того, для адекватного отражения связи между входом и выходом системы в системотехнике вводится понятие «состояние». По своему смыслу состояние z(τ) представляет собой совокупность существенных свойств (характеристик) системы, знание которых в настоящем (в момент времени τ) позволяет определить ее поведение в будущем (в моменты времени t > τ). Благодаря этому понятию, уравнение “вход-выход”-состояние принимает вид:

Y_T = A(T, z(τ), X_T), (2.1)

где X_T, Y_T - входной и выходной процесс на интервале времени T;

A(*)- оператор выходов.

Согласно (2.1), выходной процесс полностью определяется входным процессом и начальным состоянием и не зависит от того, каким образом система была переведена в это состояние. Отсюда ясно, что уравнение (2.1) ограничивает класс рассматриваемых систем только такими системами, функционирование которых в настоящем не зависит от того, как они функционировали в прошлом.

Для полного описания процесса функционирования системы необходимо задать условия определения состояния системы. Для этого вводится понятие уравнения состояния:

z(t) = B(τt, z(τ), X_τt), (2.2)

где

B(*) - оператор, устанавливающий однозначную зависимость z(t) от пары (z(τ), X_τt), которая задана на интервале t, и называемый оператором перехода.

Уравнения (2.1) и (2.2) имеют достаточно логичное обобщение и на многомерный случай, когда каждая из компонент уравнений имеет векторный вид:

Таким образом, модель функционирования системы должна обеспечивать прогнозирование процесса функционирования на всем интервале функционирования T (множество времени) по заданному вектору начального состояния записанном в векторном виде входному процессу (T). Согласно изложенному выше, для решения этой задачи достаточно задать множества допустимых значений входных X и выходных Y процессов, а также множество возможных состояний системы Z и операторы выхода A и перехода B. Модель функционирования системы без предыстории представляет собой кортеж

MF = <T, X, Y, Z, A, B>. (2.3)

Если все компоненты в (2.3) известны, модель функционирования полностью определена и может быть использована для описания и изучения свойственных системе процессов функционирования.

Модель вида (2.3) называется общесистемной моделью. Несмотря на многообразие свойств компонентов кортежа (2.3) удается выделить ряд особенностей, которые позволяют конкретизироваться характер функционирования системы:

1) Если интервал функционирования системы Т = [ ] представляет отрезок оси действительных чисел, заданный началом и концом , то система функционирует в непрерывном времени. Если, кроме того непрерывны операторы А и В, то система наз. непрерывной.

2) Если реакция системы на совместное воздействие 2-ух любых внешних воздействий равна сумме реакций на каждое их этих воздействий, приложенных к системе в отдельности, то система называется линейной. - принцип суперпозиции.

3) Если при фиксированном начальном состоянии Z(t₀) система одинаково реагирует на эквивалентные, отличающиейся только сдвигом по времени входными воздействиями, то система называется стационарной.

4) Если в модели М операторы А и В каждой паре (X, V, Z(t₀)) (вход, состояние) ставят в соответствие единственные значения Y и Z, описываемая этой моделью система называется детерминированной.

Бехтин, вопрос 5.

Классификация системных моделей

Модель функционирования системы должна обеспечивать прогнозирование процесса функционирования на всем интервале функционирования T (множество времени) по заданному вектору начального состояния записанном в векторном виде входному процессу (T). Согласно изложенному выше, для решения этой задачи достаточно задать множества допустимых значений входных X и выходных Y процессов, а также множество возможных состояний системы Z и операторы выхода A и перехода B. Модель функционирования системы без предыстории представляет собой кортеж

MF = <T, X, Y, Z, A, B>. (2.3)

Если все компоненты в (2.3) известны, модель функционирования полностью определена.

Модель вида (2.3) называется общесистемной моделью.

MNLCP - легко мат.описание

MNLCP - нет адекватного мат.описания (трудно)

Инверсия (N) – данное свойство не выполняется, например, в системе нет свойства непрерывности

M – модель

N – непрерывность

L – линейность

C – стационарность

D - стохостичность

Общесистемная и системные модели функционирования (в дальнейшем термин «модель функционирования» для краткости может заменяться термином «модель» с сохранением исходного смысла) обладают исключительно высокой степенью общности, необходимой для теоретических исследований и полезны, так как выявляют общие закономерности, присущие весьма широкому классу систем.

В инженерной практике применяют конструктивные модели. Конструктивные модели в сущности представляют собой алгоритмы, пользуясь которыми, можно определить значения одних переменных, характеризующих данную систему, по заданным или измеренным значениям других переменных.

Таким образом, наиболее важные и принципиальные этапы построения модели функционирования системы определяются процессом реализации системотехнической цепочки преобразований «общесистемная модель системная модель конструктивная модель машинная модель».

КМ – может и должна вырастать из большой общей системной модели путем конкретизации ее свойств.

При построении моделей функционирования систем применяют следующие подходы:

1. непрерывно-детерминированный подход, описание идет через ДУ и получают (дифференцированные уравнения, D-схемы);

2. дискретно-детерминированный (применяют теорию конечных автоматов, P-схемы);

3. дискретно-стохастический подход (вероятностные автоматы, D-схемы);

4. непрерывно-стохастический подход (системы СМО – системы массового обслуживания, Q-схемы)

5. обобщенный / универсальный подход (агрегитивные системы A-схемы)

Бехтин, вопрос 6. Непрерывно детерминированные модели (д - схемы).

Рассмотрим особенности непрерывно детерминированного подхода на примере, используя в качестве Матем Моделей дифференциальные уравнения.

Дифференциальными уравнениями называются такие уравнения, в которых неизвестными будут функции одной переменной или нескольких переменных, причём в уравнение входят не только их функции, но их производные различных порядков.

Пусть имеем уравнение, связывающее входную и выходную величины:

(1)

Уравнение (1) называется уравнением «вход-выход».

линейная стационарная система с одним входом и одним выходом

Решение уравнения (1) зависит от K(t), от начальных условий . Эти координаты определяют начальное состояние системы.

Левую часть приводят к уравнению 1-го порядка путем введения переменных состояния: , где - переменные состояния. Тогда

(2)

Уравнение (2) представлено в нормальной форме Коши, которое можно записать в матричной форме: (3) уравнение в пространстве состояний, где

z – вектор-столбец переменных состояния:

, необходимое условие ;

- матрица коэффициентов координат состояния;

- матрица коэффициентов входных воздействий;

, - некоторые числовые матрицы.

Сопоставляя уравнения (2) и (3) получим числовые матрицы:

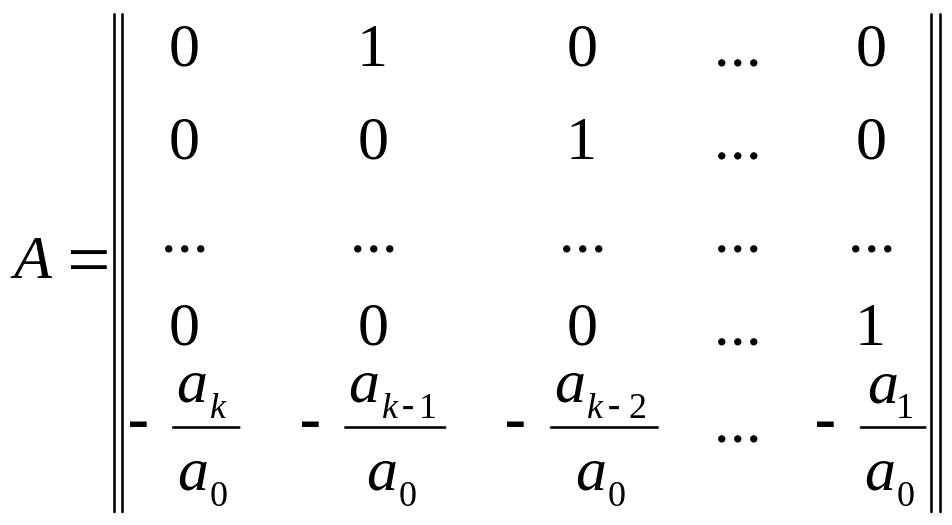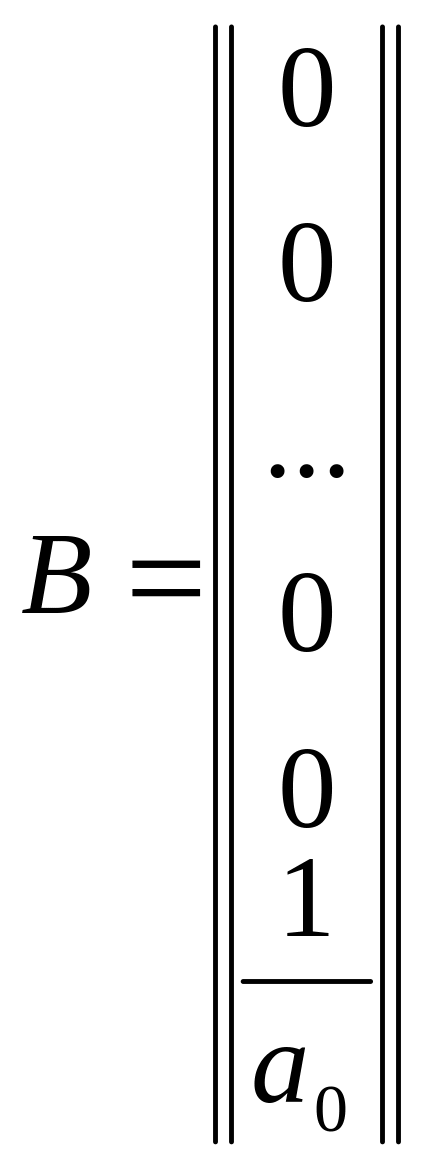; ; ; D = 0. (4)

В общем случае, когда передаточная функция системы

имеет полиноминальные функции ,

, где , то матрица А определяется выражением (4), а матрица В имеет вид: где

Бехтин, вопрос 7.

ДИСКРЕТНО-ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ (F-СХЕМЫ)

Особенности дискретно-детерминированного подхода на этапе формализации процесса функционирования систем рассмотрим на примере использования в качестве математического аппарата те­ории автоматов. Теория автоматов — это раздел теоретической кибернетики, в котором изучаются математические модели — авто­маты. На основе этой теории система представляется в виде авто­мата, перерабатывающего дискретную информацию и меняющего свои внутренние состояния лишь в допустимые моменты времени. Понятие «автомат» варьируется в зависимости от характера конк­ретно изучаемых систем, от принятого уровня абстракции и целесо­образной степени общности.

Основные соотношения. Автомат можно представить как некото­рое устройство (черный ящик), на которое подаются входные сиг­налы и снимаются выходные и которое может иметь некоторые внутренние состояния. Конечным автоматом называется автомат, у которого множество внутренних состояний и входных сигналов (а следовательно, и множество выходных сигналов) являются конеч­ными множествами.

Абстрактно конечный автомат (англ. finite automata) можно представить как математическую схему (F-схему), характеризующу­юся шестью элементами: конечным множеством X входных сиг­налов (входным алфавитом); конечным множеством Y выходных сигналов (выходным алфавитом); конечным множеством Z внут­ренних состояний (внутренним алфавитом или алфавитом состоя­ний); начальным состоянием z₀, z_oєZ; функцией переходов ; функцией выходов . Автомат, задаваемый F-схемой: ,— функционирует в дискретном автоматном време­ни, моментами которого являются такты, т. е. примыкающие друг другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния. Обозначим состояние, а также входной и выходной сигналы, соответствующие t-му такту при t=0, 1, 2..., через z(t), x(t), y(t). При этом, по условию, z(0)=z_o, a , , .

Абстрактный конечный автомат имеет один входной и один выходной каналы. В каждый момент t=0, 1, 2, ... дискретного времени F-автомат находится в определенном состоянии z(t) из множества Z состояний автомата, причем в начальный момент времени t=0 он всегда находится в начальном состоянии z(0)=z_o. В момент t, будучи в состоянии z(t), автомат способен воспринять входном канале сигнал и выдать на выходном канале сигнал , переходя в состояние , , . Абстрактный конечный автомат реализует некоторое отображение множества слов входного алфавита X на множество слов выходного алфавита Y. Другими словами, если на вход конечного автомата, установленного в начальное состояние z₀, подавать в некоторой последовательности буквы входного алфавита x(0), х(1), х(2),..., т. е. входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита у(0), у(1), y(2),..., образуя выходное слово.

Таким образом, работа конечного автомата происходит по сле­дующей схеме: в каждом t-м такте на вход автомата, находящегося состоянии z(t), подается некоторый сигнал x(t), на который он реагирует переходом в (t+1)-м такте в новое состояние z(t+l) выдачей некоторого выходного сигнала. Сказанное выше можно описать следующими уравнениями: для F-автомата первого рода, называемого также автоматом Мили,

(2.13_8)

(2.14_9)

для F-автомата второго рода

(2.15_10)

(2.16_11)

Автомат второго рода, для которого

(2.17_12)

т.е. функция выходов не зависит от входной переменной х (t),

называется автоматом Мура.

Таким образом, уравнения (8) — (12), полностью задающие автомат, являются частным случаем, когда система S детерминированная и на ее единственный вход поступает дискретный сигнал X.

По числу состояний различают конечные автоматы с памятью и без памяти. Автоматы с памятью имеют более одного состоя­ния, а автоматы без памяти (комбинационные или логические схе­мы) обладают лишь одним состоянием. При этом, согласно (2.14), работа комбинационной схемы заключается в том, что она ставит в соответствие каждому входному сигналу x(t) определенный вы­ходной сигнал y(t), т. е. реализует логическую функцию вида

Эта функция называется булевой, если алфавиты X и Y, кото­рым принадлежат значения сигналов х и у, состоят из двух букв.

Бехтин, вопрос 8.

Дискретно-детерминированные модели (F-схемы). Примеры задания автоматов Мили и Мура.

Система представляется в виде авто­мата, перерабатывающего дискретную информацию и меняющего свои внутренние состояния лишь в допустимые моменты времени.

По характеру отсчета дискретного времени конечные автоматы делятся на синхронные и асинхронные. В синхронных F-aвmoматах моменты времени, в которые автомат «считывает» входные сигналы, определяются принудительно синхронизирующими сигна­лами. После очередного синхронизирующего сигнала с учетом «счи­танного» и в соответствии с уравнениями (8) — (12) происходит переход в новое состояние и выдача сигнала на выходе, после чего автомат может воспринимать следующее значение входного сиг­нала. Таким образом, реакция автомата на каждое значение вход­ного сигнала заканчивается за один такт, длительность которого определяется интервалом между соседними синхронизирующими сигналами. Асинхронный F-автомат считывает входной сигнал непрерывно, и поэтому, реагируя на достаточно длинный входной сигнал постоянной величины х, он может, как следует из (8) — (12), несколько раз изменять состояние, выдавая соответствующее число выходных сигналов, пока не перейдет в устойчивое, которое уже не может быть изменено данным входным сигналом.

Чтобы задать конечный F-автомат. необходимо описать все элементы множества , т. е. входной, внутренний и выходной алфавиты, а также функции переходов и выходов, причем среди множества состояний необ­ходимо выделить состояние z₀, в котором автомат находился в мо­мент времени t=0. Существует несколько способов задания работы F-автоматов, но наиболее часто используются табличный, графи­ческий и матричный.

Простейший табличный способ задания конечного автомата основан на использовании таблиц переходов и выходов, строки которых соответствуют входным сигналам автомата, а столбцы -его состояниям. При этом обычно первый слева столбец соответ­ствует начальному состоянию z₀. На пересечении i-й строки и к-го столбца таблицы переходов помещается соответствующее значе­ние функции переходов, а в таблице выходов -соответствующее значение функции выходов. Для F-автомата Мура обе таблицы можно совместить, получив так называемую отмеченную таблицу переходов, в которой над каждым состоянием z_k автомата, обозначающим столбец таблицы, стоит соответствующий этому состоянию, согласно (2.17), выходной сигнал .

Описание работы F-автомата Мили таблицами переходов и выходов иллюстрируется табл. 1, а описание F-автомата Мура - таблицей переходов (табл. 2).

Таблица 1.

xl	zk
	z0	z1	…	zk
Переходы
x1			…
x2			…
…	…	…	…	…
xl			…
Выходы
x1			…
x2			…
…	…	…	…	…
xl			…

Таблица 2.

xl
			…
			…
x1			…
x2			…
…	…	…	…	…
xl			…

Примеры табличного способа задания F-автомата Мили F1 с тремя состояниями, двумя входными и двумя выходными сигналами приведены в табл. 3, а для F-автомата Мура F2 — в табл.4

Таблица 3.

переходы
Выходы

Таблица 4.

При другом способе задания конечного автомата используется понятие направленного графа. Граф автомата представляет собой набор вершин, соответствующих различным состояниям автомата соединяющих вершины дуг графа, соответствующих тем или иным переходам автомата. Если входной сигнал х_к вызывает переход из состояния z_i в состояние z_j, то на графе автомата дуга, соединяющая вершину z_i с вершиной z_j, обозначается х_к. Для того чтобы задать функцию выходов, дуги графа необходимо отметить соответствующими выходными сигналами. Для автоматов Мили их разметка производится так: если входной сигнал х_к действует на состояние z_i, то, согласно сказанному, получается дуга, исходящая из z_i| и помеченная х_k; эту дугу дополнительно отмечают выходным сигналом . Для автомата Мура аналогичная разметка графа такова: если входной сигнал х_k действуя на некоторое состо­яние автомата, вызывает переход в состояние z_j, то дугу, направлен­ную в z_j и помеченную x_k, дополнительно отмечают выходным сигналом .

На рис. 2.3, а, б приведены заданные ранее таблицами F-автоматы Мили F1 и Мура F2 соответственно.

a)

б)

П ри решении задач моделирования систем часто более удобной формой является матричное задание конечного автомата. При этом матрица соединений автомата есть квадратная матрица С=||С_ij||, строки которой соответствуют исходным состояниям, а столбцы — состояниям перехода. Элемент с_и=x_к/y_s, стоящий на пересечении i-й строки и j-го столбца, в случае автомата Мили соответствует вход­ному сигналу x_к, вызывающему переход из состояния z_i в состояние z_j, и выходному сигналу y_s выдаваемому при этом переходе. Для автомата Мили F1 рас­смотренного выше, матрица соединений имеет вид

Если переход из состояния z_i в состояние z_j происходит под действием нескольких сигналов, элемент матрицы с_ij представляет cобой множество пар «вход-выход» для этого перехода, соединенных знаком дизъюнкции.

F-автомата Мура элемент c_ij равен множеству входных сигналов на переходе , а выход описывается вектором выходов

Ψ компонента которого — выходной сигнал, отмечающий состояние z_i

Пример 2.2. Для рассмотренного выше F-автомата Мура F2 запишем матрицу соединений и вектор выходов:

;

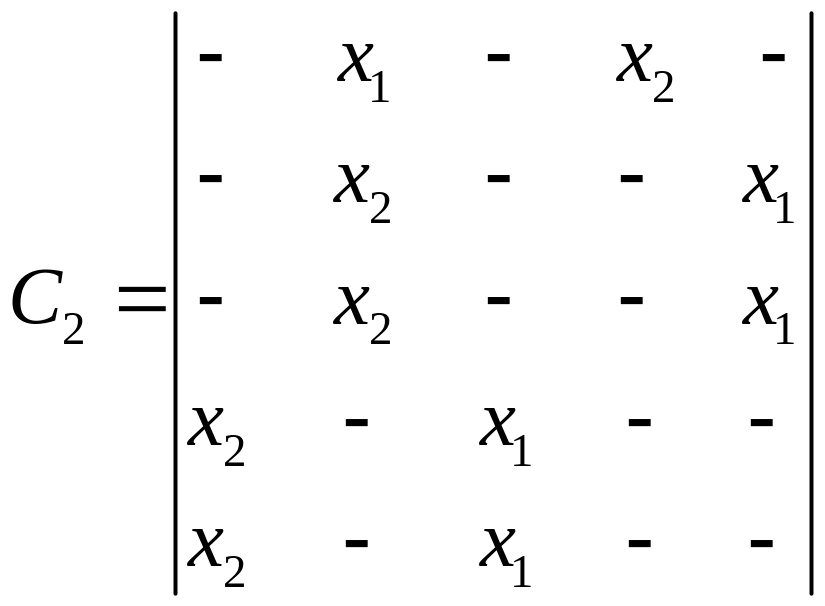Для детерминированных автоматов выполняется условие однозначности переходов: автомат, находящийся в некотором состоянии под действием любого входного сигнала не может перейти более чем в одно состояние. Применительно к графическому способу задания F-автомата это означает, что в графе автомата из любой вершины не могут выходить два ребра и более, отмеченные одним и тем же входным сигналом. Аналогично этому в матрице соединений автомата С в каждой строке любой входной сигнал не должен встречаться более одного раза.

Для F-автомата состояние z_k называется устойчивым, если для любого входа для которого , имеет место, . Таким образом,F-автомат называется синхронным, если каждое его состояние устойчиво.

Бехтин, вопрос 9,10.

Дискретно-стохастические модели (P-схемы).

Описываются через вероятностный автомат (ВА) - дискретный потактный преобразователь информации с памятью, функционирова­ние которого в каждом такте зависит только от состояния памяти в нем и может быть описано статистически.

Схемы вероятностных автоматов (Р-схем) применяются:

• в проектировании дискретных систем, проявляющих статистически закономерное случайное пове­дение;

• в определении алгоритмических возможностей систем;

• в обосновании границ целесообразности их использования;

• в решении задач синтеза по выбранному критерию дискретных стохастических систем, удовлетворяющих заданным ограничениям.

Математическое понятие Р-автомата формируется на понятиях, введенных для F-автомата.

Пусть множество G, элемен­тами которого являются всевозможные пары , где x_i и z_s — элементы входного подмножества X и подмножества состояний Z соответственно . Если существуют две такие функции и , что с их помощью осуществляются отображения и , то говорят, что

(1)

определяет конечный автомат детерминиро­ванного типа.

Введем общую математическую схему. Пусть Ф — множество всевозможных пар вида (z_k, y_j), где y_j — элемент выходного подмножества Y, т.е. . Пусть любой элемент множества G индуцирует на множестве Ф некоторый закон распределения следующего вида:

Таблица 1

Элементы из Ф	•••	(z1, y1)	•••	(z1, y2)	•••	(zK, yJ-1)	(zK, yJ)
(xi, zs)	•••	b11	•••	b12	•••	bK(J-1)	bKJ

При этом

, (2)

где b_kj — вероятности перехода автомата в состояние z_k и выдаче на выходе сигнала y_j, если автомат был в состоянии z_S и на его вход в этот момент времени поступил сигнал х_i. Число таких распределений, представленных в виде таблиц, равно числу элементов множества G.

Обозначим множество этих таблиц через В. Тогда четверка элементов (3)

называ­ется вероятностным автоматом (Р-автоматом).