
- •1. Равенство векторов
- •2. К линейным операциям над векторами относятся:
- •Операции с векторами и их свойства
- •Теорема 11.7.
- •Теорема 11.8.
- •Теорема 11.9.
- •Теорема 11.10.
- •Теорема 11.11.
- •4. Базис. Разложение векторов по базису.
- •Операции над векторами в прямоугольной системе координат.
- •Расстояние от точки до прямой
- •Канонический вид
- •Свойства определителей
- •Описание метода
- •Матричный метод
- •2.6. Собственные векторы и собственные значения
- •2.7. Собственные значения
- •2.8. Собственные векторы
- •Приведение квадратичных форм к каноническому виду
- •Теория пределов Предел последовательности
- •Предел функции
- •Первый замечательный предел
- •Второй замечательный предел
2.6. Собственные векторы и собственные значения
Пусть A — это квадратная матрица. Вектор v называется собственным вектором матрицы A, если
Av = λv,
где число λ называется собственным значением матрицы A. Таким образом преобразование, которое выполняет матрица A над вектором v, сводится к простому растяжению или сжатию с коэффициентом λ. Собственный вектор определяется с точностью до умножения на константу α ≠ 0, т.е. если v — собственный вектор, то и αv — тоже собственный вектор.
2.7. Собственные значения
У матрицы A , размерностью (N×N) не может быть больше чем N собственных значений. Они удовлетворяют характеристическому уравнению
det(A − λI) = 0,
являющемуся алгебраическим уравнением N-го порядка. В частности, для матрицы 2×2 характеристическое уравнение имеет вид
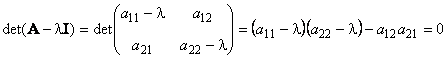
Например,

Рис. 21 Собственные значения
Набор собственных значений λ1,..., λN матрицы A называется спектром A.
Спектр обладает разнообразными свойствами. В частности
det(A) = λ1×...×λN, Sp(A) = λ1+...+λN.
Собственные значения произвольной матрицы могут быть комплексными числами, однако если матрица симметричная (At = A), то ее собственные значения вещественны.
2.8. Собственные векторы
У матрицы A, размерностью (N×N) не может быть больше чем N собственных векторов, каждый из которых соответствует своему собственному значению. Для определения собственного вектора vn нужно решить систему однородных уравнений
(A − λnI) vn = 0.
Она имеет нетривиальное решение, поскольку det(A − λnI) = 0.
Например,

Рис. 22 Собственные вектора
Собственные вектора симметричной матрицы ортогональны.
Приведение квадратичных форм к каноническому виду
Рассмотрим некоторое линейное преобразование А с матрицей .
Это симметрическое преобразование можно записать в виде:
y1 = a11x1 + a12x2
y2 = a12x1 + a22x2
где у1 и у2 – координаты вектора в базисе .
Очевидно, что квадратичная форма может быть записана в виде
Ф(х1, х2) = х1у1 + х2у2.
Как видно, геометрический смысл числового значения квадратичной формы Ф в точке с координатами х1 и х2 – скалярное произведение .
Если взять другой ортонормированный базис на плоскости, то в нем квадратичная форма Ф будет выглядеть иначе, хотя ее числовое значение в каждой геометрической точке и не изменится. Если найти такой базис, в котором квадратичная форма не будет содержать координат в первой степени, а только координаты в квадрате, то квадратичную форму можно будет привести к каноническому виду.
Если в качестве базиса взять совокупность собственных векторов линейного преобразования, то в этом базисе матрица линейного преобразования имеет вид:
.
При переходе к новому базису от переменных х1 и х2 мы переходим к переменным и . Тогда:
Тогда .
Выражение называется каноническим видом квадратичной формы. Аналогично можно привести к каноническому виду квадратичную форму с большим числом переменных.
Теория квадратичных форм используется для приведения к каноническому виду уравнений кривых и поверхностей второго порядка.
Теория пределов Предел последовательности
Число
![]() называется
пределом последовательности
называется
пределом последовательности
![]() ,
если
,
если
![]()
![]() ,
,
![]()
![]() ,
,
![]() :
:
![]() .
Предел последовательности обозначается
.
Предел последовательности обозначается
![]() .
Куда именно стремится
,
можно не указывать, поскольку
.
Куда именно стремится
,
можно не указывать, поскольку
![]() ,
оно может стремиться только к
,
оно может стремиться только к
![]() .
.
Свойства:
Если предел последовательности существует, то он единственный.

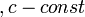
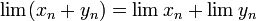 (если
оба предела существуют)
(если
оба предела существуют)
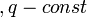
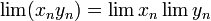 (если
оба предела существуют)
(если
оба предела существуют)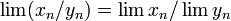 (если
оба предела существуют и знаменатель
правой части не ноль)
(если
оба предела существуют и знаменатель
правой части не ноль)Если
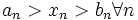 и
и
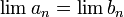 ,
то
,
то
 (теорема
«о зажатой последовательности», также
известная, как «теорема о двух
милиционерах»)
(теорема
«о зажатой последовательности», также
известная, как «теорема о двух
милиционерах»)
