4. Базис. Разложение векторов по базису.

     Определение. Базисом в пространстве Rⁿ называется любая система из n-линейно независимых векторов. Каждый вектор из Rⁿ, не входящих в базис, можно представить в виде линейной комбинации базисных векторов, т.е. разложить по базису.      Пусть – базис пространства Rⁿ и . Тогда найдутся такие числа λ₁, λ₂, …, λ_n, что .      Коэффициенты разложения λ₁, λ₂, …, λ_n, называются координатами вектора в базисе В. Если задан базис, то коэффициенты вектора определяются однозначно.      Пример. Доказать, что векторы образуют базис в R³.      Решение. Покажем, что равенство возможно только при λ₁ = λ₂ = λ₃ =0:           или      Решив систему, получим λ₁=0, λ₂=0, λ₃=0. Так как все λ_i=0 (i=1,2,3), то - линейно независимы. Они могут составить базис в R³.      Очевидно, любой новый набор из векторов может тоже быть взятым в качестве базиса в R³. Итак, базис может быть выбран неединственным образом.      Пример. Разложить вектор по базису .      Решение. . Подставим координаты всех векторов и выполним действия над ними:           Приравняв координаты, получим систему уравнений: 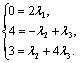          Решим ее: .      Таким образом, получим разложение: .      В базисе вектор имеет координаты .     Замечание. В каждом n-мерном векторном пространстве можно выбрать бесчисленное множество различных базисов. В различных базисах один и тот же вектор имеет различные координаты, но единственные в выбранном базисе.

Операции над векторами в прямоугольной системе координат.

С векторами, заданными в прямоугольной системе координат совершать действия еще проще, чем с их геометрическими образами. В этой статье мы покажем как выполняются операции сложения векторов и умножения вектора на число, если известны их координаты, и подробно разберем решения примеров.

Пусть на плоскости задана прямоугольная декартова система координат Oxy. Рассмотрим векторы и . Эти векторы можно разложить по координатным векторам и как и , что было показано в статье координаты вектора в прямоугольной системе координат.

Найдем сумму векторов и , а также произведение вектора на произвольное действительное число .

В силу свойств операций над векторами, справедливы следующие равенства

Правые части этих равенств представляют собой разложение векторов и по координатным векторам и , следовательно, векторы и имеют координаты и соответственно.

Аналогично для векторов и , заданных в прямоугольной системе координат Oxyz в трехмерном пространстве, мы можем записать следовательно, .

Таким образом, координаты суммы векторов и равны сумме соответствующих координат векторов и , а координаты произведения вектора на число равны соответствующим координатам вектора , умноженным на это число в заданной системе координат.

Если требуется найти координаты суммы нескольких векторов, то они будут равны сумме соответствующих координат каждого из векторов.

Уравнение прямой линии на плоскости

Определение. Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0,

причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

•  C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат

•  А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох

•  В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу

•  В = С = 0, А ≠0 – прямая совпадает с осью Оу

•  А = С = 0, В ≠0 – прямая совпадает с осью Ох

Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.