1. Равенство векторов

п.6. Равенство векторов.

Определение. Два вектора называются равными, если они сонаправленные и имеют равные модули.

Иначе, .

Равные векторы можно обозначать одной буквой (с чертой или со стрелкой): . В этом случае говорят, что вектор отложен от точки А. Если , то говорят, что вектор отложен от точки С. Таким образом, любой вектор можно отложить от любой точки пространства S.

Замечание. На самом деле, понятие равенства векторов расширяет само понятие вектора. Если первоначально под вектором мы понимали упорядоченную пару точек пространства S, т.е. направленный отрезок, то теперь под вектором мы будем понимать множество в с е х направленных отрезков, сонаправленных друг с другом и имеющих одинаковую длину. Если один и тот же вектор отложить от двух различных точек, например, , то направленный отрезок можно совместить с направленным отрезком с помощью параллельного переноса. Часто направленные отрезки и называются представителями одного и того же вектора .

2. К линейным операциям над векторами относятся:

1) умножение вектора на число (Произведением вектора a и числа α называется вектор, обозначаемый α∙a. (или наоборот a∙α), модуль которого равен |α a| =|α||a|, а направление совпадает с направлением вектора a, если α>0, и противоположно ему, если α< 0.

2) сложение векторов (Суммой векторов называется вектор, обозначаемый , начало которого находится в начале первого вектора a₁, а конец – в конце последнего вектора a_n, ломаной линии, составленной из последовательности слагаемых векторов. Это правило сложения называется правилом замыкания ломаной. В случае суммы двух векторов оно равносильно правилу параллелограмма)

Операции с векторами и их свойства

Суммой векторов и называется вектор Для любых векторов справедливы равенства

Теорема 11.6.

Каковы бы ни были три точки A , B и C , имеет место векторное равенство

Доказательство

Пусть A ( x ₁ ; y ₁ ), B ( x ₂ ; y ₂ ), C ( x ₃ ; y ₃ ) – данные точки.

Вектор имеет координаты вектор имеет координаты Следовательно, вектор имеет координаты Вектор имеет такие же координаты. По теореме 11.5 Теорема доказана.

Рисунок 11.2.1.

Рисунок 11.2.2.

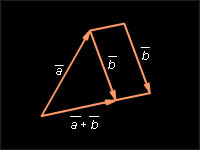
Замечание. Теорема 11.6 дает следующий способ построения суммы произвольных векторов и Надо от конца вектора отложить вектор равный вектору Тогда вектор, начало которого совпадает с началом вектора а конец – с концом вектора будет суммой векторов и

Правило параллелограмма : для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.

Рисунок 11.2.3.

Разностью векторов и называется такой вектор который в сумме с вектором дает вектор откуда c ₁ = a ₁– b ₁ ; c ₂ = a ₂– b ₂.

Произведением вектора на число λ называется вектор т. е.

• Для любого вектора и чисел λ и μ

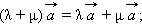
• Для любых двух векторов и и числа λ

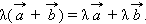
Теорема 11.7.

Абсолютная величина вектора равна |λ || a |. Направление вектора при совпадает с направлением вектора если λ > 0, и противоположно направлению вектора если λ < 0.

Доказательство

Построим векторы и равные и соответственно ( O – начало координат). Пусть и – координаты вектора Тогда координатами точки A будут числа и координатами точки B – числа и Уравнение прямой OA имеет вид: α x + β y = 0. Так как уравнению удовлетворяют координаты точки A ( a ₁ ; a ₂ ), то ему удовлетворяют и координаты точки B (λ a ₁ ; λ a ₂ ). Отсюда следует, что точка B лежит на прямой OA . Координаты c ₁и c ₂любой точки C , лежащей на луче OA , имеют те же знаки, что и координаты a ₁и a ₂точки A , и координаты любой точки, которая лежит на луче, дополнительном к OA , имеют противоположные знаки.

Поэтому, если λ > 0, то точка B лежит на луче OA , а следовательно, векторы и одинаково направлены. Если λ < 0, то точка B лежит на дополнительном луче и векторы и противоположно направлены.

Абсолютная величина вектора равна Теорема доказана.

Рисунок 11.2.4.