Определение весовой характеристике и избыточность кода. Перечислите коды с обнаружение ошибок. Опишите код с двойной проверкой на чётность.
Весовая характеристика – определяет количество слов с одинаковым весов (единиц).
Избыточность кода - позволяет обеспечивать надежную защиту системы и ее помехоустойчивость. увеличивая избыточность кода, можно обеспечить такие условия, при которых декодирующее устройство сможет не только обнаружить ошибки в приеме отдельных символов, но и исправить часть этих ошибок.
Коды с обнаружение ошибок: инверсный код, код с проверкой на чётность, код Хэмминга, Линейный код общего вида, декодирование.
Код с двумя проверками на нечётность – если количество единиц в коде чётное, то пишем , если нет то 1 и повторяем ещё раз.
Перечислите основные понятия алгебры логики. Определения логической функции и высказыванию. Опишите три способа задания булевых функций.
Основные понятия алгебры логики: высказывание, таблица истинности, логический элемент, логическая схема.
Логическая функция – функция которая может быть задана формулой в которой указана последовательность логических операций.
Высказывание – это всякое суждение, которое может принимать одно из значений правда (1), ложь (0).
Три способа задания булевых функций: а) Табличный (таблица истинности)
б) логическая функция F={x1,x2,x3,..,xn}
в) логическая схема (УГО)
19. Определение логическая функция и высказывание. Перечислите и опишите основные законы и тождество алгебры логики.
Логическая функция – функция которая может быть задана формулой в которой указана последовательность логических операций.
Высказывание – это всякое суждение, которое может принимать одно из значений правда (1), ложь (0).
Основные законы и тождество алгебры логики:
К
оммутативные
Ассоциативные
Дистрибутивные
Законы инверсии
Законы повторения
Законы отрицания
Закон двойного отрицания
З
аконы
поглощения
Правила для операций с константами
Операция склеивания
Операция неполного склеивания
Определение таблица истинности. Назовите элементы булевой функции от одной и нескольких переменных. Опишите их приведите УГО.
Таблица истинности – слева перечисленные все возможные комбинации аргументов, справа значение функций.
Б
улевые
функции
1. Функция константа 0
2
.
Функция Y=f(X)=X - функция повторения.
3
.Функция
Y=f(X)=NOT(X) - отрицание НЕ
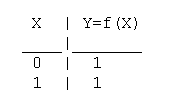
4
.Функция
константа 1
5. Логическое ИЛИ (логическое сложение, дизъюнкция):
Y= X1 + X2 = X1VX2
6
.Логическое
И (логическое умножение, конъюнкция,
схема совпадений):
Y = X1X2 = X1&X2
7
.Функция
стрелка Пирса (ИЛИ-НЕ):
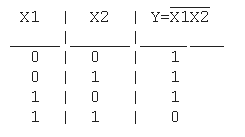
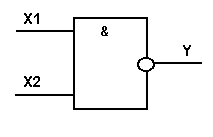
8.Функция штрих Шеффера (И-НЕ)
Определение ранг логической функции. Назовите канонические формы представления логической функции. Сформулируйте правило записи СДНФ по таблице истинности.
Ранг логической функции - количество переменных функции.
Канонические формы представления логической функции: СКНФ и СДНФ.
Правило
записи СДНФ:
В ячейках результата 
отмечаются
лишь те комбинации, которые приводят
логическое выражение в состояние
единицы.
Далее
рассматриваются значения переменных
при которых функция равна 1. Если значение
переменной равно 0, то она записывается
с инверсией. Если значение переменной
равно 1, то без инверсии.
Определение ранг логической функции. Назовите канонические формы представления логической функции. Сформулируйте правило записи СКНФ по таблице истинности.
Ранг логической функции - количество переменных функции.
Канонические формы представления логической функции: СКНФ и СДНФ.
Правило
записи СКНФ: В
ячейках строки́
отмечаются
лишь те комбинации, которые приводят
логическое выражение в состояние нуля.
В дизъюнкцию записывается переменная
без инверсии если она в наборе равна 0
и с инверсией если она равна 1. Первый
член СКНФ рассматриваемой функции
выглядит так: 
.
Определение логический базис. Виды логических базисов. Назначение комбинационных схем.
Логический базис - набор простейших функций.
Виды логических базисов: И, ИЛИ, И-НЕ, ИЛИ-НЕ
Назначение комбинационных схем: предназначены для преобразования дискретной информации, при чём значение выходных сигналов однозначно определяются значению входных сигналов.
Определение сокращенной ДНФ. Методы минимизации ФАЛ. Опишите метод непосредственных преобразований.
Сокращенная ДНФ – функция, которая получается из сокращения ДНФ, путём выполнения склеивания и поглощения конъюнкции.
Методы минимизации ФАЛ: карты Карно, Квайна-Мак-Класски, Метод непосредственных преобразований, Квайна.
Метод непосредственных преобразований: При решении схемы методом непосредственного преобразования элементов используют серию эквивалентных преобразований схемы, направленных на упрощение схемы.
При применении данного метода: а) Записываются ДСНФ логических функций б) Форма преобразуется и упрощается с использованием аксиом алгебры логики. При этом, выявляются в исходном ДСНФ в которых есть по одной не совпадающей переменной. По отношению к соседних импликантами применяется закон склейки.