Список литературы

1. Балаш В.А.. Задачи по физике и методы их решения. Пособие для учителей.– М.: Просвещение, 1974.

2. Беликов Б.С.. Решение задач по физике. Общие методы. – М.: Высшая школа, 1986.

3. Беспалько В.П. Слагаемые педагогической технологии. – М.: Педагогика, 1989.

4. Бугаев А.И. Методика преподавания физики в средней школе. Теоретические основы.– М.: Просвещение, 1981.

5. Гальперин П.Я. Формирование умственных действий. Хрестоматия по общей психологии: Психология мышления. – М., 1981.

6. Каменецкий С.Е., Орехов В.П.. Методика решения задач по физике в средней школе. Пособие для учителей. – М.: Просвещение, 1971.

7. Кротов В.М. К вопросу о сложности (трудности) физических задач. Фiзiка: праблемы выкладання — №3. — 1999.

8. Крохина И.Г.. Анализ условий задач // Физика №21/04

9. Немов Р.С.. Психология в 3 книгах. Книга 1. Общие основы психологии. – М.: ГИЦ «Владос», 1998.

10. Основы методики преподавания физики в средней школе / Под ред. Перышкина А.В., Разумовского В.Г., Фабриканта В.А. [Разумовский В.Г., Бугаев А.И., Дик Ю.И. и др.] – М.: Просвещение, 1984.

11. Поверина И.А. Алгоритм // Физика №9/05

12. Подольский А.И.. Психологическая система П.Я. Гальперина. /Вопросы психологии. 2002. №5

13. Теория и методика обучения физике в школе: Общие вопросы / Под ред. С.Е. Каменецкого, Н.С. Пурышевой. – М.: Академия, 2000.

14. Усова А.В., Тулькибаева Н.Н.. Практикум по решению физических задач. – М.: Просвещение, 1992.

15. Физика. Теория и технология решения задач / В.А. Бондарь, Д.И. Кульбицкий, А.А. Луцевич и др.; Под общ. ред. В.А. Яковенко. – Мн.: ТетраСистемс, 2003.

16. Фридман Л.М. Логико-психологический анализ школьных учебных задач. – М.: Педагогика, 1977.

Приложение 1. Тестовые задачи по физике

1. Механика

1.1 Основы кинематики

1 . Движение двух тел заданы графически. Тогда относительная скорость движения второго тела _отн равна:

1) -6 м/с 2) -0,6 м/с 3) -0,1 м/с

4) 0,1 м/с 5) 6 м/с

2. Пловец переплывает реку шириной h под углом β к берегу. Если его скорость относительно берега υ = 1 , ширина реки h=40м и смещение пловца по течению реки l =40м, то угол β равен:

1) 22,5˚ 2) 30˚ 3) 45˚ 4) 60˚ 5) 90˚

3. Эскалатор метро поднимает неподвижно стоящего на нем человека за t₁=1,5 мин. Если по неподвижному эскалатору человек поднимается за t₂=3 мин, тогда по движущемуся эскалатору человек на подъем затратит время t₃ (с), равное: (60)

4. Самолет летит из пункта А в пункт В, расстояние между которыми S=900 км, и обратно со скоростью _с=300 км/ч относительно воздуха. Если вдоль линии полета непрерывно дует ветер со скоростью _в=60 км/ч, то на весь полет самолет затратит время t (выраженное в минутах), равное: (375)

5. Скорость моторной лодки по течению равна υ₁ = 1,1 , а против течения υ ₁ = 0,9 . Какова скорость течения воды в реке?

1) 0,1 м/с 2) 0,2 м/с 3) 0,3 м/с 4) 0,4 м/с 5) 0,5 м/с

6. Если моторная лодка проходит расстояние S=16 км между двумя пунктами на реке вниз по течению за время t₁=5,0 ч, а против течения – за t₂=8,0 ч, то модуль скорости движения лодки _л относительно воды равен:

1) 0,3 2) 0,6 3) 1,3 4) 2,6 5) 5,2

7. На рисунке приведена зависимость координаты тела от времени. Путь и проекция перемещения тела за первые t=2с движения составляют:

1) 2м,-2м 2) 2м,2м 3)1м, -2м 4) 2м,1м 5)2м, -1м

8. Два шарика начали одновременно двигаться в одном направлении из точек А и В, находящихся на расстоянии =5 м друг от друга. Шарик из т.А догнал шарик из т. В через время t=25 с. Если скорость шарика, движущегося из т. В _в=0,8 м/с, то скорость шарика, движущегося из т. А _а (м/с), равна: (1)

9. Из двух пунктов, расстояние между которыми = 100м, одновременно начали двигаться навстречу друг другу два тела. Они встретились через t= 4с. Если скорость одного из них ₁= 20 м/с, тогда скорость второго тела ₂ (м/с) будет равна: (5)

10. Cкорость катера υ_к= 7м/c, скорость течения реки υ_т= 3м/c. Когда катер двигался против течения, с него в воду опустили поплавок. Затем катер прошел против течения s=4,2 км, повернул обратно и догнал поплавок. Общее время t движения катера составляет:

1) 28 мин 2) 45мин 3) 54мин 4) 35мин 5) 48мин

11. Из одного пункта в другой мотоциклист двигался со скоростью ₁= 72км/ч, а на обратном пути скорость его движения составила ₂=36 км/ч. Какова средняя скорость мотоциклиста на всем пути?

1 )40 км/ч 2) 48 км/ч 3) 54 км/ч 4 )60 км/ч 5) 64 км/ч

12. Первую половину времени движения вертолет перемещался на север со скоростью υ₁= 30м/c, а вторую половину времени - на восток со скоростью υ₂= 40м/c. Разность между средней путевой скоростью и модулем скорости перемещения составляет:

1) 5м/с 2) 10м/с 3) 15м/с 4) 20м/с 5) 8м/с

13. Первую половину времени тело движется со скоростью υ₁= 6м/c под углом α₁=45˚ к оси Ох, а вторую половину времени - под углом α₂=135˚к этой же оси со скоростью υ₂= 9м/c. Средняя скорость перемещения равна:

1) 7,5м/с 2) 11м/с 3) 1,5м/с 4) 5,4м/с 5) 7,2м/с

14. Велосипедист ехал из одного города в другой. Половину пути он проехал со скоростью υ₁= 12км/ч. Затем половину оставшегося времени он ехал со скоростью υ₂= 6км/ч, а затем до конца пути со скоростью υ₃= 4км/ч.

Средняя скорость велосипедиста на всем пут составляет:

1) 11км/ч 2) 7,7км/ч 3) 7км/ч 4) 5,5км/ч 5) 8,4км/ч

15. Дорога между городами А и В состоит из подъема на возвышенность и спуска с неё. Рейсовый автобус на подъеме по этой дороге идет со скоростью 36 км/ч, а на спуске 54 км/ч. Какова средняя скорость движения автобуса на всем пути, если длина подъема и спуска одинаковы?

1) 11м/с 2) 12м/с 3) 12,5 м/с 4) 13,5м/с 5) 14м/с

16. Два тела выходят из одного пункта в одном направлении через t₁=20с одно после другого и двигаются с одинаковым ускорением. Если расстояние между ними в s=240 м будет через время t=40 с, то они движутся с ускорением a, равным:

1) 0,2 м/с² 2) 0,3 м/с² 3) 0,4 м/с² 4) 0,5 м/с² 5) 0,6 м/с²

1 7. Автомобиль, трогаясь с места, движется равноускоренно с ускорением а=2 м/с², тогда путь s, пройденный автомобилем за третью секунду t=3 с, равен:

1) 2 м 2) 3 м 3) 5 м 4) 6 м 5) 8 м

18. График зависимости проекции скорости тела _х от времени t представлен на рисунке. Тогда путь s, пройденный телом, равен:

1 ) 0 м 2) 2 м 3) 4 м 4) 6 м 5) 8 м

19. График зависимости проекции скорости тела _х от времени t представлен на рисунке. Тогда путь s, пройденный телом, равен:

1) 0 м 2) 2 м 3) 4 м 4) 6 м 5) 8м

20. Уравнение прямолинейного движения тела x=5+2t+0,4t² (м). Спустя t=3,0с после начала движения скорость движения тела  будет равна:

1) 2,4 м/с 2) 3,2 м/с 3) 3,8 м/с 4) 4,4 м/с 5) 4,9 м/с

21. Длина взлетной полосы =720 м, скорость самолета при взлете =216 км/ч, тогда ускорение а самолета равно:

1) 0,08 м/с² 2) 1,24 м/с² 3) 2,50 м/с² 4) 3,24 м/с² 5) 5,0 м/с²

22. Два тела движутся по одной прямой согласно уравнениям х₁= -4+2t+t² и х₂= 6-8t+t².Относительная скорость υ_о тел в момент встречи равна:

1) 0 м/с 2) 3 м/с 3) 7 м/с 4) 6 м/с 5) 10 м/с

23. По наклонной доске пустили снизу вверх шарик. Если на расстоянии l=30 см от начала движения шарик побывал дважды через t₁=1с и t₂=2с после начала движения, то начальная скорость υ₀ шарика составляет:

1) 45 см/с 2) 30 см/с 3) 60 см/с 4) 20 см/с 5) 10 см/с

24. Координата материальной точки изменяется согласно уравнению

х = – 2+6t- 0,25t². Средняя скорость < υ > точки за первые t=10с движения равна:

1) 0 м/с 2) 3,3 м/с 3) 6 м/с 4) 3,1м/с 5) 3,5 м/с

25. Пассажир, стоявший у начала третьего вагона электрички, определил, что начавший двигаться вагон прошел мимо него за t₁=5с, а вся электричка за t₂=15,8с. Сколько вагонов у электрички?

1) 9 2) 10 3) 11 4) 12 5)13

26. Мяч, отскочивший от поверхности земли вертикально вверх со скоростью =10 м/с, пролетел мимо окна высотой h=1,5м за t=0,2с. Высота h₀ относительно поверхности земли, на которой расположен подоконник, составляет:

1) 2,8м 2) 1,6м 3) 1,4м 4) 2,0м 5) 1,8м

27. Свободно падающее тело за последнюю секунду прошло путь s=15 м, тогда оно падало с высоты h, равной:

1 )10 м 2) 15 м 3) 18 м 4) 20 м 5) 24 м

28. Парашютист, спускающийся с постоянной скоростью υ₁= 5м/c, находясь на высоте h=100м, бросил вертикально вверх небольшое тело со скоростью υ₂= 10м/c относительно себя. Интервал времени ∆t между падением тела и приземлением парашютиста составит:

1) 20с 2) 16,8с 3) 14,4с 4) 24,2с 5) 32,4с

29. Камень падает в ущелье. Через промежуток времени ∆t=6с слышен звук удара камня о землю. Если скорость звука υ_з= 330м/c, то глубина ущелья h составляет:

1) 150м 2) 55м 3) 660м 4) 242м 5) 110м

30. Если тело, свободно падающее с некоторой высоты, первый участок пути пролетело за время t₁=1с, а такой же последний за t₂=0,5с, то высота h, с которой падало тело, составляет:

1) 6,8м 2) 7,8м 3) 10м 4) 9,8м 5) 8,6м

31. С какой скоростью υ должен лететь самолет по шестидесятой параллели, чтобы прибыть в пункт назначения раньше по местному времени, чем он вылетел из пункта отправления? Радиус Земли принять равным R=6370 км.

1) 738 км/ч 2) 785 км/ч 3) 833 км/ч 4) 864 км/ч 5) 890 км/ч

32. Какая относительная погрешность показаний спидометра автомобиля, если вместо «нормальных» колёс поставили колёса с радиусом на 10% больше?

1) 0,05 2) 0,07 3) 0,09 4) 0,11 5) 0,13

33. Магнитная лента движется в магнитофоне с постоянной скоростью. Каково относительное изменение частоты вращения приемной катушки кассеты, если радиус намотки за время прослушивания кассеты увеличился в n=3 ?

1) 1/6 2 ) 1/4 3) 1/3 4) 2/3 5) 3/4

34. Цилиндр радиусом r= 20см вращается вокруг своей оси с частотой ν=1/π с-¹. Вдоль образующей цилиндра движется тело с постоянной скоростью υ=30 см/с относительно его поверхности. Какова скорость тела относительно неподвижной системы отсчета?

1) 0,4 м/с 2) 0,5 м/с 3) 0,6 м/с 4) 0,7 м/с 5) 0,8 м/с

35.Диаметр колеса велосипеда d=70 см., ведущая зубчатка его имеет n₁= 48 зубьев, а ведомая n₂=18 зубьев. С какой скоростью υ движется велосипедист на этом велосипеде при частоте вращения педалей ν= 1с^-1?

1) 5м/с 2) 6,28 м/с 3) 6,65 м/с 4) 6,82 м/с 5) 7,14 м/с

36. С какой частотой ν велосипедист должен вращать педали велосипеда, чтобы двигаться со скоростью υ=6,28 м/с, если диаметр колеса велосипеда d=50 см, ведущая зубчатка имеет n₁= 48 , а ведомая n₂=15 зубьев?

1) 0,75 с ^-1 2) 1 с ^-1 3) 1,25 с ^-1 4) 1,5 с ^-1 5) 1,75 с ^-1

37. Зубчатое колесо диаметром D₁=50 см находится во внешнем зацеплении с зубчатым колесом диаметром D₂=30 см. Оба колеса вращаются вокруг неподвижных осей. Если число оборотов первого колеса за время t=1с равно n₁=3, то число оборотов второго колеса n₂ за это же время будет равно:

1) 2 2) 3 3) 4 4) 5 5) 6

38. За время свободного падения с высоты h=5 м волчок совершил N=10 оборотов, вращаясь с угловой скоростью , равной:

1) 3,14 рад/с 2) 6,28 рад/с 3) 31,4 рад/с 4) 62,8 рад/с 5) 628 рад/с

39. Металлический шарик бросают под углом α=30˚ к горизонту с начальной скоростью υ₀=16 . Если не учитывать сопротивление воздуха, то скорость шарика через время t=0,6с от начала движения υ равна… (14)

40. С высоты H горизонтально бросают со скоростью υ₀ =5 железный шарик. Если не учитывать сопротивление воздуха и дальность полета шарика по горизонтали l=5м, то высота H равна…м (5)

41. Если тело брошено с земли под углом  к горизонту с начальной скоростью_о,, то графиком зависимости вертикальной проекции скорости _у от координаты х (расстояния по горизонтали от места бросания) будет график:

1) 1 2) 2 3) 3 4) 4 5) 5

42. Из шланга, расположенного около поверхности земли, вырывается струя воды. Если шланг медленно вращать вокруг вертикальной оси и одновременно с этим изменять угол его наклона к земле, и максимальная площадь, которую можно полить S=314 м² , то модуль скорости вырывания струи воды из шланга  равен:

1) 5 2) 8 3) 10 4) 11 5) 12

43. Тело брошено с поверхности земли с начальной скоростью υ₀=10 . Если через ∆t==0,5с скорость тела составила υ₁=8,1 , то максимальная высота h, на которую поднимается тело в процессе движения, равна:

1) 1,8м 2) 3,6м 3) 0,9м 4) 2,7м 5) 1,2м

44. Камень брошен горизонтально со склона горы, образующего угол α=45˚ с горизонтом. Если камень упал на склон на расстоянии l=50м от точки бросания, то его начальная скорость υ₀ составляла:

1) 10 2) 13,3 3) 12,4 4) 31,4 5) 18,3

45. Мальчик бросает в стену мяч со скоростью v₀=10 под углом α=45˚ к горизонту, стоя на расстоянии l₁=4м от стены. Удар мяча о стенку упругий. Чтобы затем поймать отскочивший мяч, мальчик должен стать от стены на расстоянии l₂ равном:

1) 2м 2) 4м 3) 3м 4) 8м 5) 6м

46. Камень брошен с вышки горизонтально. Когда камень опустился по вертикали на ∆h= 20м, его скорость оказалась направленной под углом α=45˚ к горизонту. Начальная скорость υ₀ камня равна:

1) 36 2) 24 3) 18 4) 20 5) 31

47. Два тела одновременно брошены из одной точки. Начальная скорость первого тела υ₁=10 и направлена вертикально вверх, второго υ₂=20 и направлена под углом α=30˚ к горизонту. Через ∆t=1с после начала движения расстояние s между телами составит:

1) 17,3м 2) 8,7м 3) 10м 4) 19,6м 5) 14,2м

48. Тело, брошенное горизонтально со скоростью υ₁=4,9 с высоты h=5м, за время своего падения совершит перемещение:

1) 8,3м 2) 25м 3) 7м 4) 9,9м 5) 5м

49. Груз массой m=100г колеблется на пружине жесткостью k=90Н/м. Какова максимальная скорость движения груза υ_м, если амплитуда колебаний х_м =3см.?

1) 0,7м/с 2) 0,8м/с 3) 0,9м/с 4) 1м/с 5) 1,1м/с

50. Движение тела описывается уравнением м. Амплитуда ускорения тела а_м равна:

1) 2) 3) 4) 5)

51. Маленький шарик на нити длиной l= 40см совершает гармонические колебания. Какова максимальная скорость движения шарика, если амплитуда колебаний х_м = 2 см?

1) 2 см/ с 2) 4 см/ с 3) 6 см/ с 4) 8 см/с 5) 10 см/с

52. Рыболов заметил, что за t= 10с поплавок совершил на волне N=20 колебаний, а расстояние между соседними горбами волн s=1,2м. Какова скорость распространения волн?

1) 2,0 м/ с 2) 2,4 м/ с 3) 2,8 м/ с 4) 3,0 м/с 5) 3,4 м/с

53. Математический маятник длиной l=90см колеблется с амплитудой x_м=3 см. За какое время он пройдет путь равный s=1,5см, если в начальный момент времени маятник проходит положение равновесия?

1) 0,6 π с 2) 0,3 π с 3) 0,1 π с 4) 0,05 π с 5) 0,01 π с

54. Скорость звука в воде υ=1450 м/с. На каком расстоянии находятся ближайшие точки, колеблющиеся в противофазе, если частота колебаний равна ν=725 Гц?

1) 0,5 м 2) 1 м 3) 1,5 м 4) 2 м 5) 3 м

55. Длина звуковой волны в воздухе для самого низкого мужского голоса достигает λ=4,3м. Если скорость звука в воздухе υ_з= 344м/с, то частота ν колебаний этого голоса равна:

1) 70Гц 2) 80Гц 3) 90Гц 4) 95Гц 5) 100Гц

56. В неподвижном лифте математический маятник имеет период колебаний Т=3,0 с. Если период колебаний в движущемся лифте равен Т₁=3,6 с, то лифт движется с ускорением а, равным:

1) 2,5 м/с² 2) 2,8 м/с² 3) 3,1 м/с² 4) 3,3 м/с² 5) 3,8 м/с²

57. В неподвижном автомобиле математический маятник имеет период колебаний Т. Если автомобиль двигается с ускорением а= 5 м/с² по горизонтальному участку пути и период колебаний математического маятника Т₁ =2,86 с, то период колебаний в неподвижном автомобиле Т равен:

1) 2,8 с 2) 3,0 с 3) 3,2 с 4) 3,6 с 5) 4,2 с

58. Амплитуда колебаний математического маятника x_м=6 см, максимальная скорость движения _м=20 см/с, тогда длина маятника  равна:

1) 0,9 м 2) 0,8 м 3) 0,7 м 4) 0,6 м 5) 0,5 м

59. Если груз массой m=200 г подвешен на пружине, жесткость которой k=3,2 Н/м, и совершает гармонические колебания с амплитудой х_м=5,0 см, то груз проходит положение равновесия со скоростью , равной:

1) 0,12 м/с 2) 0,18 м/с 3) 0,20 м/с 4) 0,25 м/с 5) 0,32 м/с

60. Груз, подвешенный к резиновому шнуру, колеблется вдоль вертикальной оси. Как изменится период колебаний груза, если его подвесить на том же шнуре, сложенном вдвое?

1) уменьшится в 2 раза 2) увеличится в 2 раза 3) уменьшится в 4 раза 4) увеличится в 4 раза 5) не изменится

61. Как изменится длина звуковой волны при переходе ее из воздуха в воду? Скорость звука в воде υ₁= 1500м/с, а в воздухе υ₂= 340 м/с.

1) не изменится 2) увеличится в 4,4 раза 3) увеличится в 2,2 раза 4) уменьшится в 4,4 раза 5) уменьшится в 2,2 раза

62. Материальная точка совершает гармонические колебания. Если амплитуда ускорения материальной точки а_м=16м/с² и частота колебаний ν= Гц, то амплитуда скорости υ_м равна:

1) 0,04м/с 2) 0,08м/с 3) 0,4м/с 4) 0,6м/с 5) 0,8м/с

63. Материальная точка совершает гармонические колебания. Если период колебаний T=0,314с и амплитуда координаты х_м=0,04м, то амплитуда скорости материальной точки υ_м равна

1) 0,04м/с 2) 0,08м/с 3) 0,4м/с 4) 0,6м/с 5) 0,8м/с

64. Если материальная точка совершает гармонические колебания, представленные на графике зависимости х(t), то частота колебаний  равна

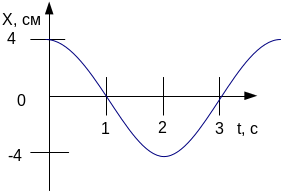1) 0,2 Гц 2) 0,3 Гц 3) 0,5Гц 4) 2 Гц 5) 5 Гц

65. Амплитуда колебаний математического маятника х_м=6 см, длина маятника =90 см, тогда максимальная скорость движения _м равна:

1) 0,1 м/с 2) 0,2 м/с 3) 0,3 м/с 4) 0,4 м/с 5) 0,5 м/с

66. По поверхности воды в озере волна распространяется со скоростью υ=9 м/с. Каков период колебаний T бакена на воде, если длина волны λ=4,5 м?

1) 0,1 с 2) 0,2 с 3) 0,3 с 4) 0,4 с 5)0,5 с

67. Движение тела описывается уравнением м. Если в момент времени t=0,5с модуль скорости тела υ= , то наименьшая начальная фаза колебательного движения тела φ₀ равна:

1) 2) 3) 4) 5)

68. Движение тела описывается уравнением м. Если в момент времени t=0,5с модуль скорости тела υ = , то циклическая частота колебаний груза равна:

1) 1с^-1 2) с^-1 3) с^-1 4) с^-1 5) 2 с^-1

69. Движение тела описывается уравнением м. В момент времени t=0,5с проекция скорости тела υ_х равна:

1) 1 2) 3) - 4) - 5)

70. Груз массой m= 1кг на пружине жесткостью k= 90 Н/м совершает колебания. Какое максимальное ускорение движения груза, если амплитуда колебаний x_м=3 см?

1) 1,8м/с 2) 2,7 м/с 3) 3,1 м/с 4) 3,6 м/с 5) 4,2 м/с