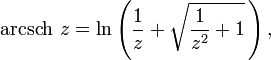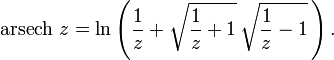- •Вопрос 16. Теорема Дирихле разложимости функций в ряд Фурье
- •Вопрос 17-18. Ряд Фурье чётных и нечётных функций.
- •Вопрос 19-20. Ряд Фурье функций для периодичных функций с произвольным периодом 2l и непериодических функций заданных на интервале [a;b]
- •Вопрос 21. Комплексная форма рядов Фурье
- •Основные свойства криволинейного интеграла 2-го рода.
- •Вычисление криволинейного интеграла 2-го рода
- •Вопрос 23. Формула Грина
- •Вопрос 24. Комплексные числа в тригонометрической, показательной форме. Действия над ними.
- •Вопрос 25. Расширенная комплексная плоскость. Сфера Римана. Понятие бесконечно удаленно точки
- •Вопрос 26. Линии и области на комплексной плоскости
- •Вопрос 27. Понятие функции комплексного переменного
- •Вопрос 28. Предел и непрерывность функции комплексной переменной
- •Вопрос 29. Показательная функция, ее свойства
- •Вопрос 30. Функция sin z, cos z , их свойства
- •Вопрос 31. Гиперболическая функция, ее свойства, связь с тригонометрической функцией
- •Вопрос 32. Логарифмическая функция, ее свойства
- •Вопрос 33. Обратные тригонометрические функции
- •Вопрос 34. Обратные гиперболические функции
Вопрос 31. Гиперболическая функция, ее свойства, связь с тригонометрической функцией
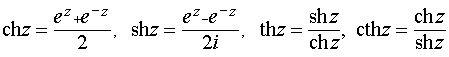
Из сравнения их с тригонометрическими функциями следует, что между тригонометрическими и гиперболическими функциями существуют следующие соотношения: ch z = cos(i z), sh z = - isin (i z), th z = - i tg (i z ), cth z = i ctg (i z).
Отсюда, в частности, вытекает, что
ch2 z - sh2 z = [cos(iz)]2 + [sin(iz)]2 = 1.
Гиперболические функции выражаются через тригонометрические функции от мнимого аргумента.
![]() .
.
![]() .
.
Вопрос 32. Логарифмическая функция, ее свойства
![]()
Если значение логарифма, равное l n | z | + i аrg z , назвать главным значением и обозначить его l n z , то для Ln z будем иметь
![]() , где k = 0, ±
1, ± z , … .
Отсюда следует, что каждое комплексное
число, отличное от нуля и бесконечности,
имеет бесконечное множество логарифмов
(то есть значений логарифмической
функции), из которых любые два различаются
на целое, кратное
.
, где k = 0, ±
1, ± z , … .
Отсюда следует, что каждое комплексное
число, отличное от нуля и бесконечности,
имеет бесконечное множество логарифмов
(то есть значений логарифмической
функции), из которых любые два различаются
на целое, кратное
.
Итак, логарифм имеет смысл для любого ненулевого комплексного числа, в частности и для отрицательных действительных чисел. Например,
![]() .
.
Правила логарифмирования произведения и частного сохраняют свою силу:
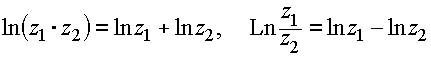
Вопрос 33. Обратные тригонометрические функции
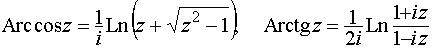 .
.
Вопрос 34. Обратные гиперболические функции
![]()
![]()
![]()
![]()