Вопрос 27. Понятие функции комплексного переменного

По необходимости для теории функций комплексного переменного к конечным (собственным) комплексным числам прибавляют бесконечность - именуется несобственным комплексным числом. Комплексная поскость с присоединенной к ней бесконечно удаленной точкой имеет название расширенной комплексной плоскости. Окрестность бесконечно удаленной точки определяется неравенством .

Предположим, что существуют две расширенные комплексные плоскости: комплексных чисел , соответственно.

О: Под функцией комплексного переменного (ФПК) понимают соответствие, которое существует между множествами и , и которое предполагает, что для каждого имеется одно или несколько . Для первого случая предствляется в качестве однозначной, во втором — многозначной функции ( ) .

Множество именуется областью определения, называется областью значений функции.

Для функции характерно наличие действительной и минимальной части. Используя , получаем . Относительно тригонометрической формы к.ч. запишем:

 

 

Пример: являет собой ФПК.

Поскольку , то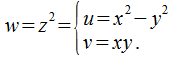

Если рассматривать ФПК -прообразом.

О: Однолистным отображние множества в и существует взаимно однозначное соответствие.

Вопрос 28. Предел и непрерывность функции комплексной переменной

Число   называется пределом функций   при   и обозначается   если для любого   найдется   такое, что для всех   удовлетворяющих неравенству  , выполняется неравенство 

Говорим, что  , если для любого R > 0 найдётся   такое, что для всех   таких, что  , выполняется неравенство 

Следует иметь в виду, что для данной функции   существование предела по любому фиксированному пути ( ) ещё не гарантирует существование предела   при  . 

Пример 1 

Пусть   Показать, что   не существует 

Для предела при   по любому лучу   имеем 

т. е. эти пределы различны для различных направлений - они запол-няют сплошь отрезок [-1, 1], и, следовательно, 

не существует

Функция   называется непрерывной в точке   если она определена в этой точке и   

Функция  , непрерывная в каждой точке области D, называется непрерывной в этой области. 

Функция   называется равномерно непрерывной в области D, если для любого   найдется   такое, что для любых точек   и   из области D таких, что  , выполняется неравенство  .

Вопрос 29. Показательная функция, ее свойства

Из определения показательной функции следует, что она не обращается в нуль ни при какомz . Функция e^z обладает периодом   , так как при изменении z на   значение функции не изменяется. Действительно, 

  .

Она удовлетворяет обозначенным ниже свойствам:

1⁰.

2⁰.

3⁰.

Вопрос 30. Функция sin z, cos z , их свойства

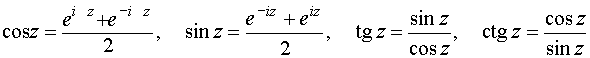
Из определения тригонометрических функций вытекает, что cos z  –  чётная функция, а sin z  –  нечётная функция, так как

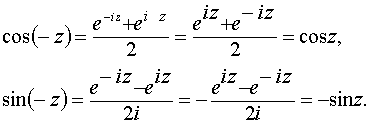
        Из определения же следует, что c o s z и   s i n z обладают периодом    , так как при изменении z на   аргументы показательных функций в правых частях формул изменяются на ±    –  величины периодов показательной функции, а значит значение функций не изменится.

        Можно показать, что все известные из тригонометрии соотношения для тригонометрических функций действительного аргумента сохраняются и в комплексной области. Однако свойство ограниченности функций уже не имеет место.