Вопрос 16. Теорема Дирихле разложимости функций в ряд Фурье

Достаточным условием разложимости функции в ряд Фурье является теорема Дирихле.

Пусть функция периода удовлетворяет следующим условиям:

1. непрерывна на интервале 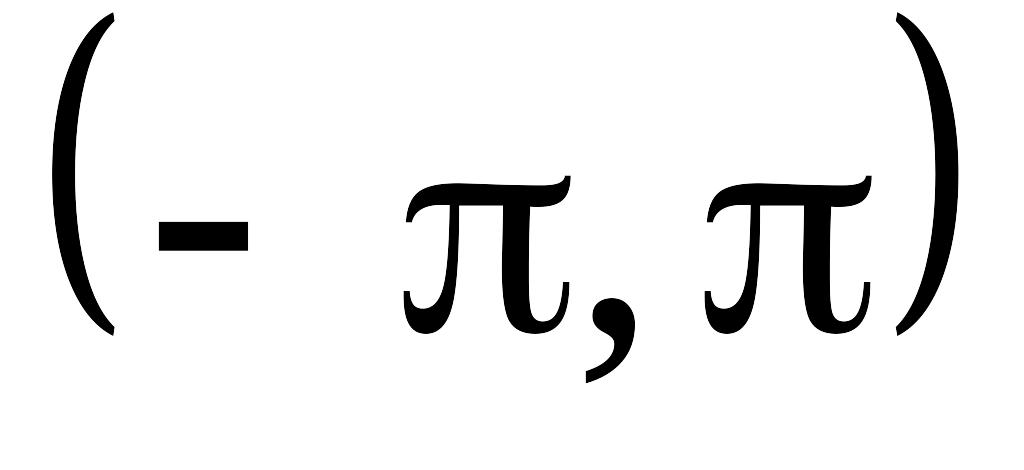всюду, за исключением конечного числа точек разрыва первого рода (т.е точек, в которых существуют конечные пределы слева 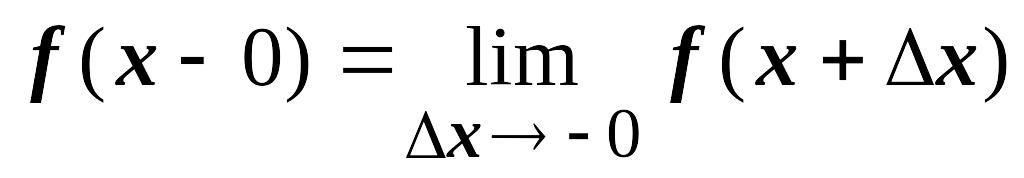и справа 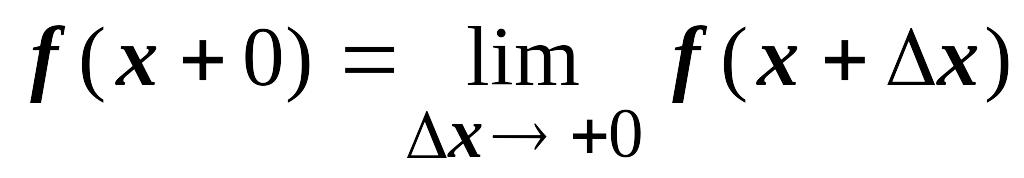, не равные друг другу);

2. Имеет на этом интервале конечное число экстремумов.

Тогда ряд Фурье сходится в каждой точке отрезка . Его сумма равна

в точках непрерывности этой функции;

в точках разрыва этой функции;

в точках .

Условия 1-2 принято называть условиями Дирихле.

Вопрос 17-18. Ряд Фурье чётных и нечётных функций.

Если - чётная функция, то произведение - функция нечётная, и по известному свойству определённого интеграла от нечётной функции, .

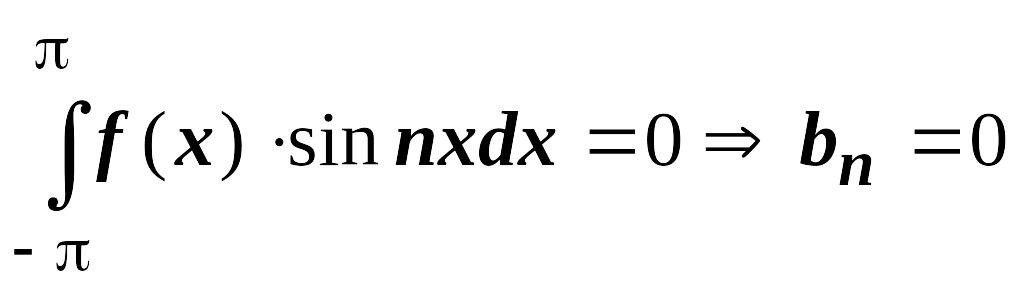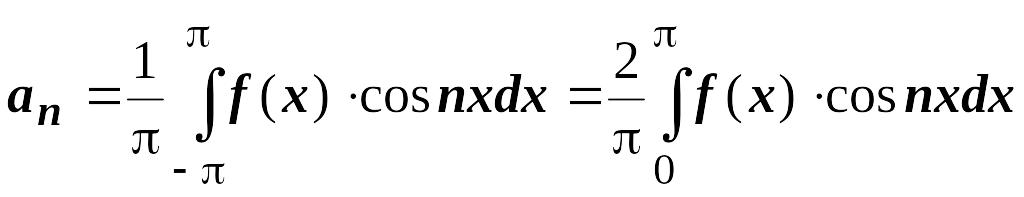Произведение в этом случае - функция чётная, поэтому . Итак, для чётных функций .

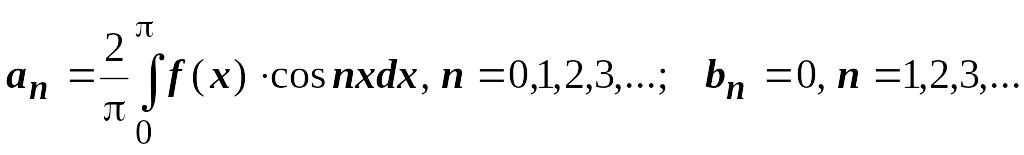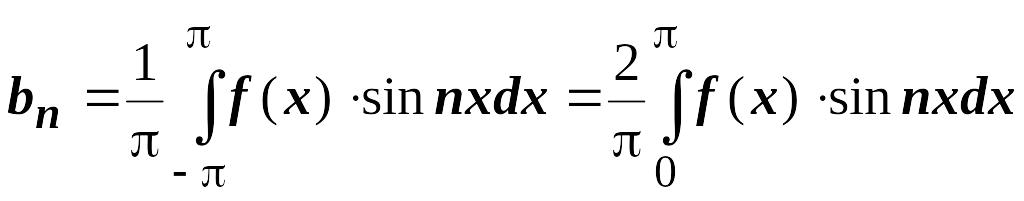Если - нечётная функция, то произведение - функция нечётная, поэтому . Произведение - функция чётная, поэтому . Итак, для нечётных функций .

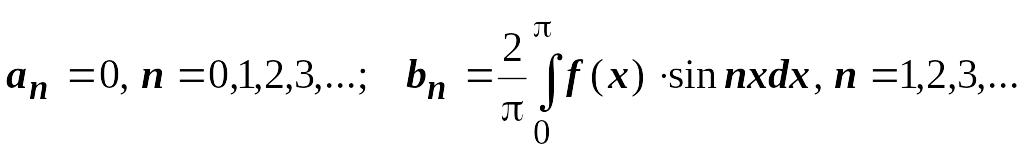Вопрос 19-20. Ряд Фурье функций для периодичных функций с произвольным периодом 2l и непериодических функций заданных на интервале [a;b]

Пусть теперь требуется разложить в ряд Фурье функцию , заданную на интервале . Сделаем линейную замену независимой переменной . Если , то . В результате функция определена на интервале , и мы можем разложить её в ряд Фурь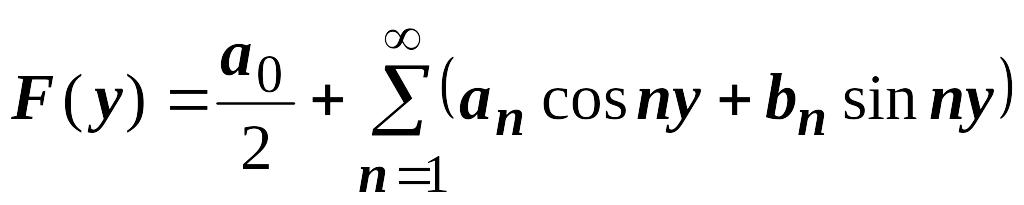е , где 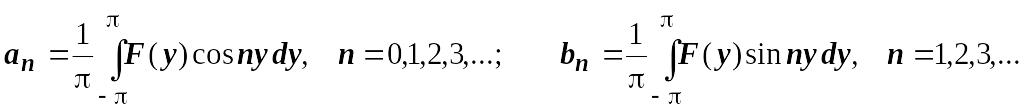Вернёмся в этих формулах к переменной х: , , .

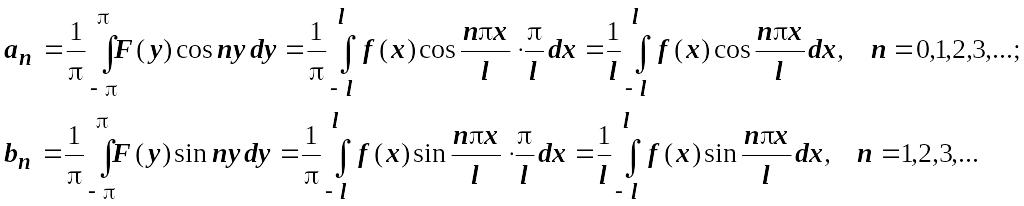
Сам ряд Фурье после перехода к переменной х запишется так: .

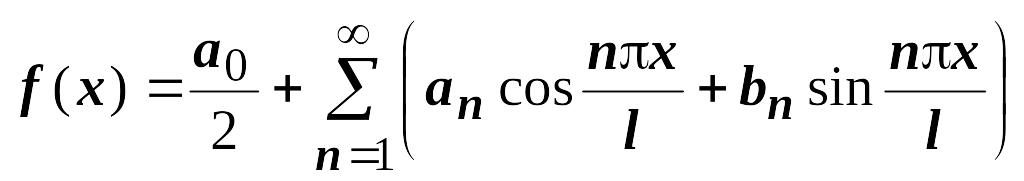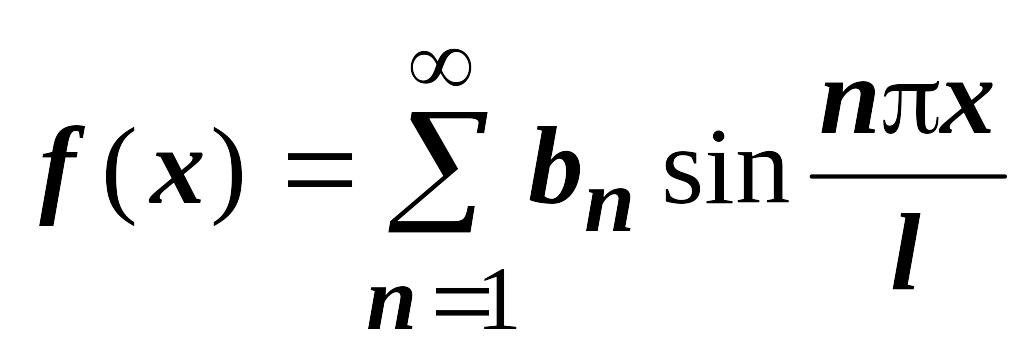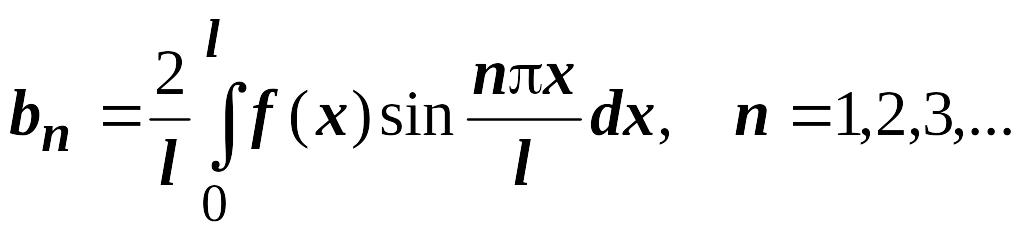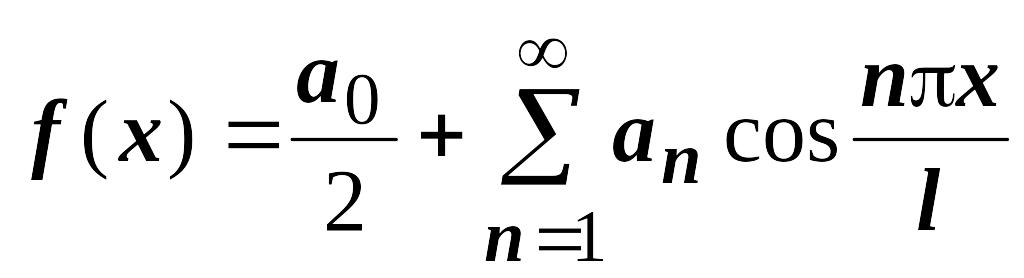Если - нечётная функция, то её разложение не будет содержать косинусов: , где . Соответственно, если - чётная функция, то её разложение не будет содержать синусов: , где .

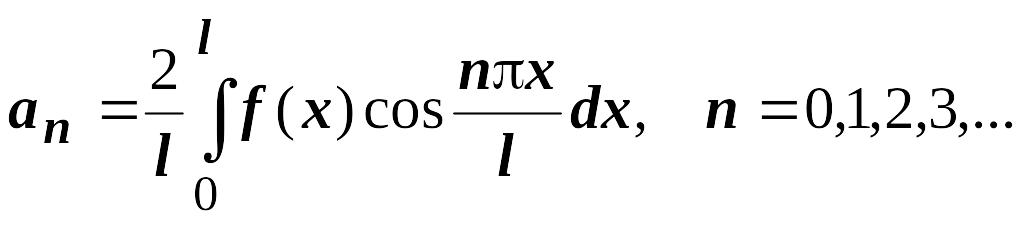Если функция f (x) определена в интервале [a,b], то ее разложение в ряд Фурье определяется той же самой формулой

где  , а коэффициенты вычисляются следующим образом:

Вопрос 21. Комплексная форма рядов Фурье

Пусть функция f (x) определена в интервале [−π, π]. Применяя формулы Эйлера

можно записать ряд Фурье данной функции в комплексной форме:

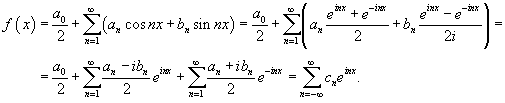
Мы использовали здесь следующие обозначения:

Коэффициенты c_n называются комплексными коэффициентами Фурье. Они определяются формулами

Если нужно построить продолжение функции f (x), имеюшей произвольный период 2L, то соответствующее выражение в комплексной форме имеет вид:

где

Комплексная форма ряда Фурье алгебраически проще и более симметрична. Поэтому, она часто используется в физике и прикладных расчетах. 

Вопрос 22. Понятие криволинейного интеграла по координатам, его свойства и вычисление в декартовой системе координат.

Криволинейный интеграл по координатам (второго рода)

Определение криволинейного интеграла второго рода

Пусть функции P(x, y) и Q(x, y) непрерывны в точках дуги АВ гладкой кривой К, имеющей уравнение  ,  .

О п р е д е л е н и е. Интегральной суммой для функций P(x, y) и Q(x, y) по координатам называется сумма вида

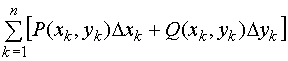, (131)

где   - проекции элементарной дуги на оси Ох и Оу.

О п р е д е л е н и е. Криволинейным интегралом по координатам (или криволинейным интегралом второго рода) от выражения P(x, y)dx + Q(x, y)dy по направленной дуге АВ называется конечный предел интегральной суммы (131) при стремлении   и   к нулю.

Это обозначается так:

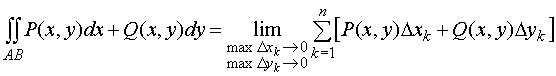. (132)