Задача 3 определение частотных и временНЫх характеристик цепи

Найдите операторную передаточную функцию H(p) активной и пассивной цепей и определите по ним частотные характеристики: амплитудно-частотную H(j) и фазочастотную (); и временные характеристики: переходную h(t) и импульсную g(t).

Для этого:

1. Выберите для своего варианта схему пассивной RL или RC цепи из табл.1.4 и рассчитайте значения ее параметров через M и N.

2. Найдите операторную передаточную функцию

или ,

где U₁(p) – L-изображение подведенного к входу цепи воздействия; U₂(p)  или I₂(p) – L-изображение искомой реакции цепи.

3. Получите по операторной передаточной функции H(p) комплексную передаточную функцию H(j) = H(p)_p=j и запишите выражения для амплитудно-частотной H(j) и фазочастотной () = = arg H(j) характеристик. Постройте графики АЧХ и ФЧХ при изменении частоты от 0 до . При построении графиков на ПК выберите наименьшее f_min = 1 Гц и наибольшее f_max значения частот такими, чтобы на графиках отображались особенности АЧХ и ФЧХ исследуемой цепи.

4. Получите выражения для временных характеристик цепи: импульсной g(t) и переходной h(t) по операторной передаточной функции. Постройте график h(t) при изменении времени от 0 до . При построении графиков на ПК выберите наименьшее и наибольшее значения времени соответственно: t_min = 1 нс, t_max = 50…200 мкс. Время t_max следует выбирать таким, чтобы на графиках было видно установившееся значение h(t).

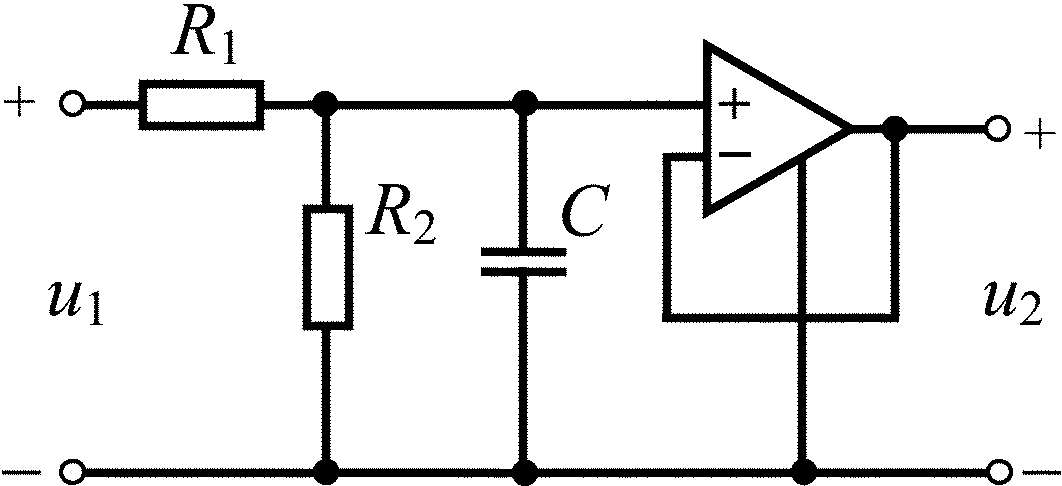
5. Выберите для своего варианта схему ARC-цепи из табл.1.5 и рассчитайте значения ее параметров через M и N. Нарисуйте схему замещения цепи, заменив условное изображение операционного усилителя (ОУ) его схемой замещения в виде ИНУН из табл. 1.6. Коэффициент усиления может быть либо сколь угодно большим (  ), либо конечным положительным или отрицательным числом K. Для полученной ARC-цепи выполните задания, указанные в пп. 2, 3, 4 задачи 3.

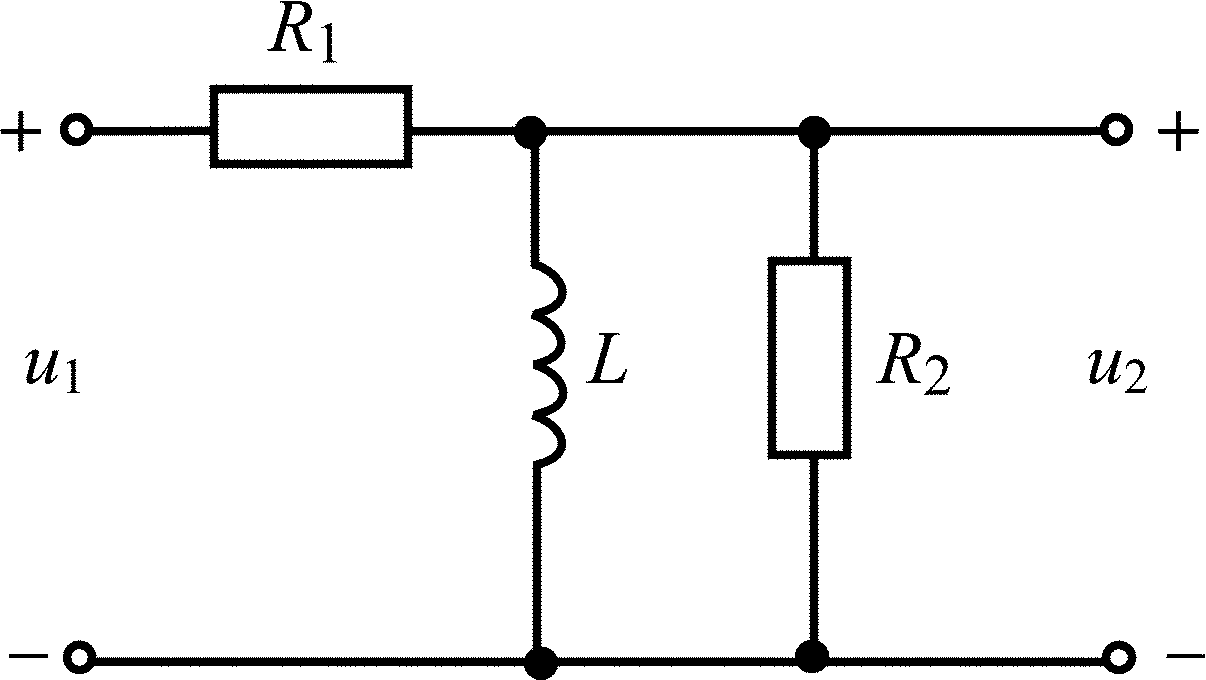
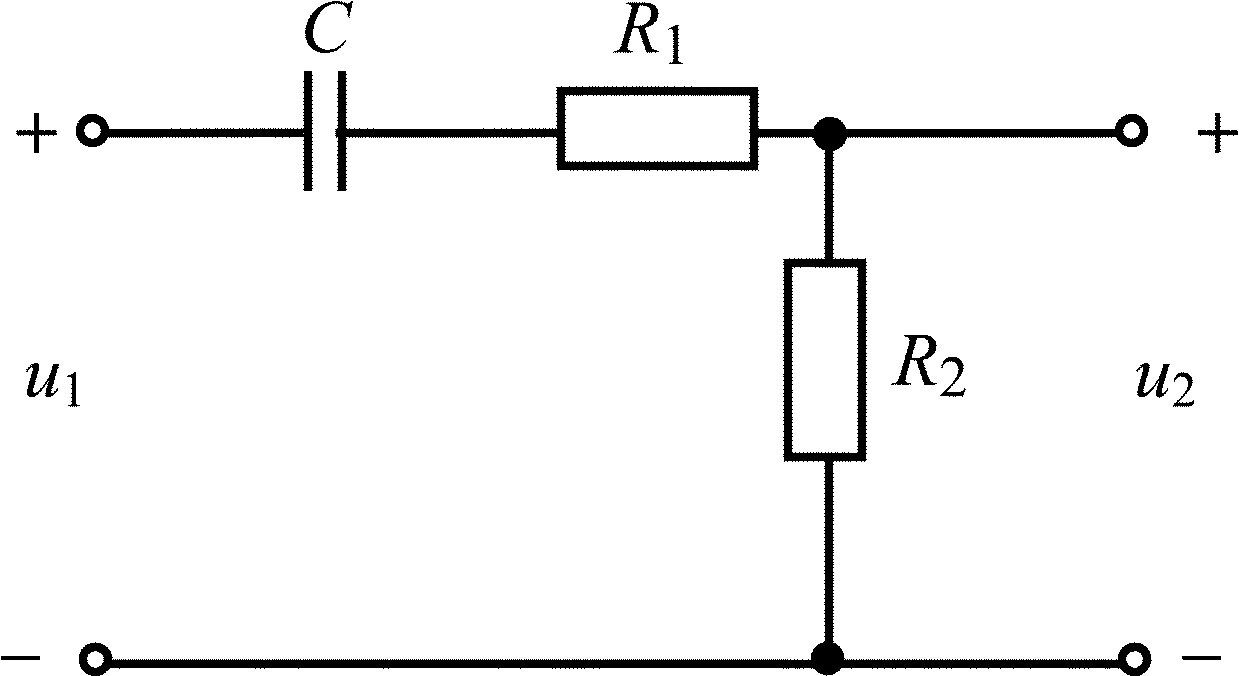
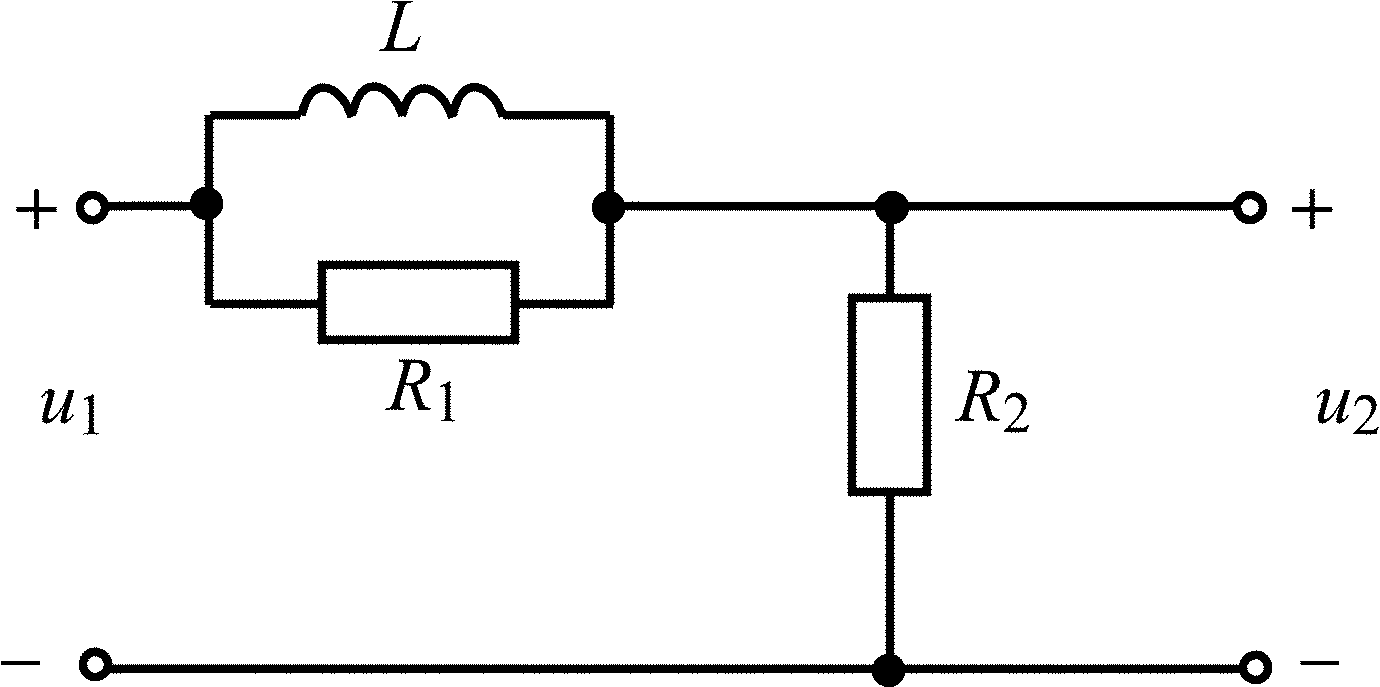
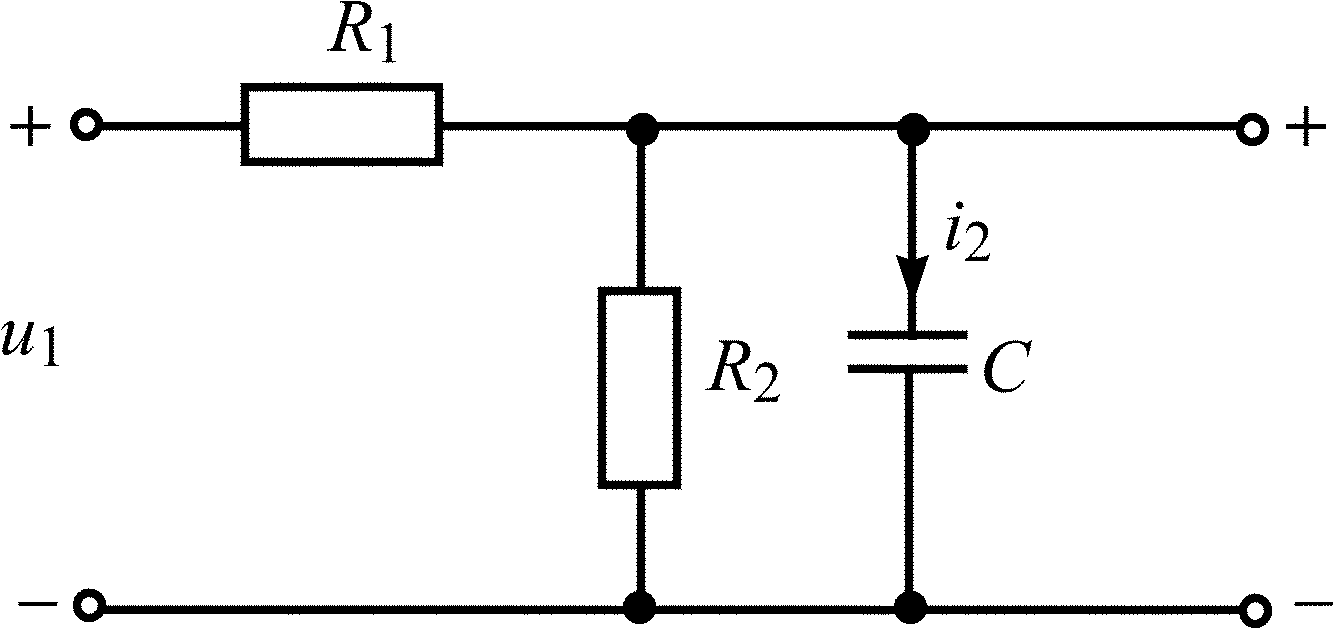
Таблица 1.4

Вариант	Схема цепи	Данные
А		R1 = R2 = (M + N), кОм L = N(M + N)2/2, мГ U0 = 0,1M, В
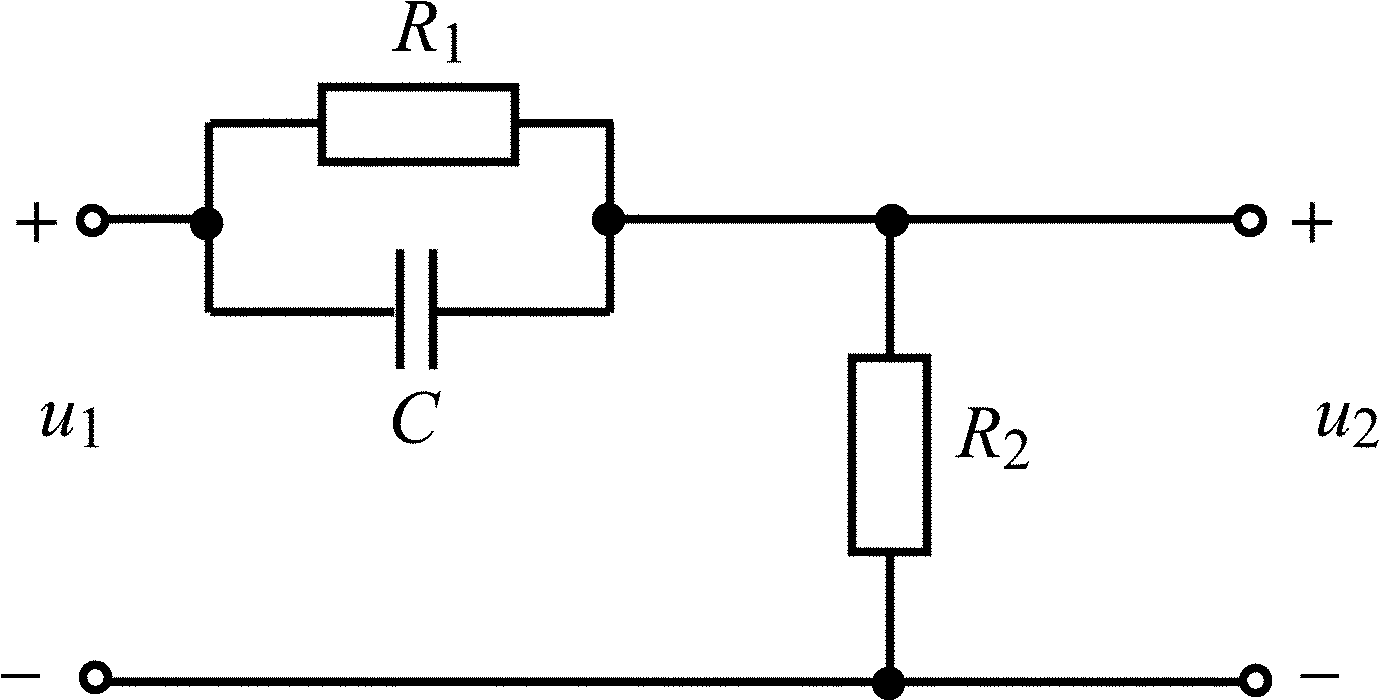
Б		R1 = R2 = (M + N), кОм С = N/2, нФ U0 = 0,1M, В
В		R1 = R2 = (M + N), кОм L = N(M + N)2/2, мГ U0 = 0,1M, В
Г		R1 = R2 = (M + N), кОм С = 2N, нФ U0 = 0,1M, В
Д		R1 = R2 = (M + N), кОм С = 2N, нФ U0 = 0,1M, В

Таблица 1.5

Вариант	Схема цепи	Данные
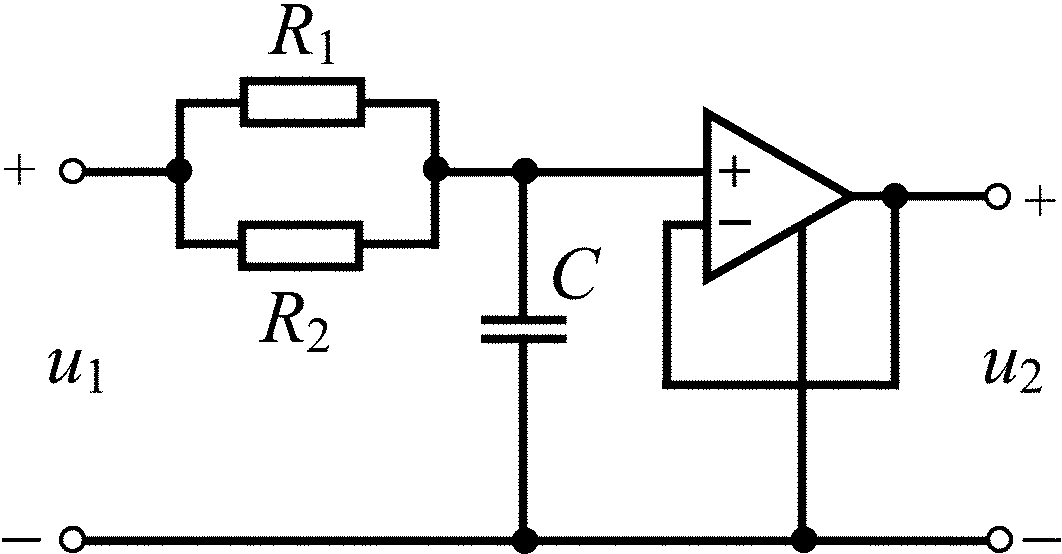
А		R1 = R2 = (M + N), кОм С = 2N, нФ U0 = 0,1M, В
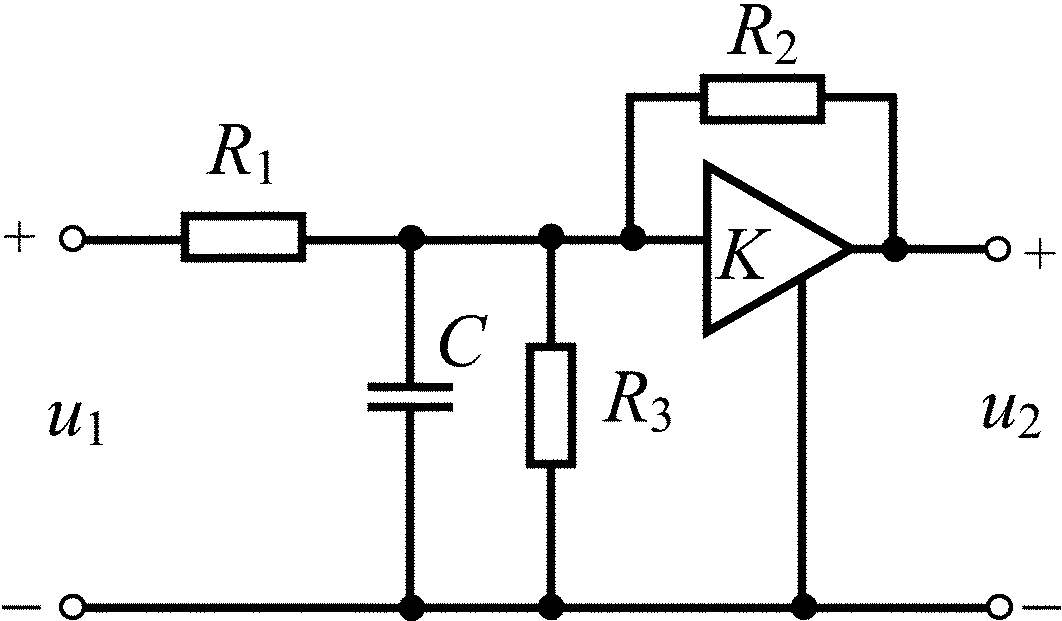
Б		R1 = R2 = R3 = (M + N), кОм С = N, нФ K = 2 U0 = 0,1M, В
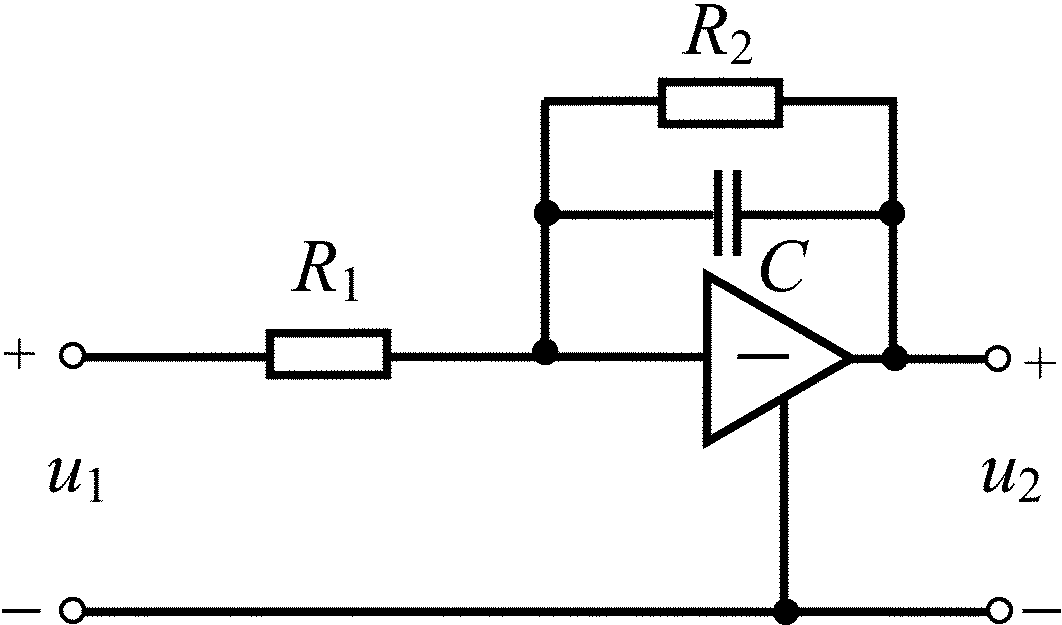
В		R1 = R2 = R3 = (M + N), кОм С = 4N, нФ K = –1 U0 = 0,1M, В
Г		R1 = R2 = (M + N), кОм С = N, нФ U0 = 0,1M, В
Д		R1 = R2 = (M + N), кОм С = 2N, нФ U0 = 0,1M, В