9.3. Полиномиальная аппроксимация [4, с. 4–8; 5, с. 41–44]

В качестве аппроксимирующей функции f(x) в задачах аналитического представления вольт-амперных характеристик нелинейных резистивных элементов очень часто используются алгебраические полиномы

той или иной степени.

Коэффициенты a₀, a₁, a₂, …, a_n представляют собой варьируемые параметры, значения которых рассчитываются так, чтобы в интервале аппроксимации a  x  b погрешность аппроксимации в соответствии с выбранным критерием «близости» не превышала допустимую _доп .

Варьируемые параметры функции f(x) будем находить методом интерполирования, который состоит в том, что выбираются дискретные точки x в интервале аппроксимации a  x  b, называемые узлами интерполирования, в которых приравниваются значения функций f(x) и x). Число узлов интерполирования выбирается равным числу варьируемых параметров аппроксимирующей функции.

Получается система n + 1 линейных уравнений

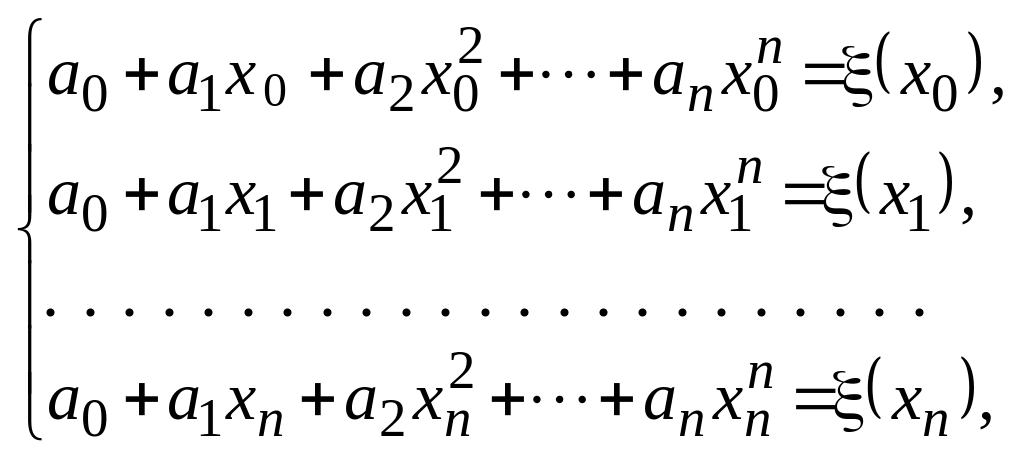
которая решается относительно неизвестных коэффициентов a₀, a₁, a₂, …, a_n.

После расчета значений варьируемых параметров осуществляется сравнение функций x) и f(x) в заданном интервале аппроксимации по выбранному критерию «близости», при этом для рассматриваемых задач необходимо, чтобы

max | f(x) – x)|  _доп.

Если допустимая погрешность аппроксимации не выполняется, то необходимо выбрать другие узлы интерполирования, и повторить расчет значений варьируемых параметров. Следует обратить внимание, что увеличение числа узлов интерполирования повышает точность аппроксимации, но при этом получается более сложная функция f(х), что приводит к усложнению решения задачи анализа нелинейной цепи.

Пример 9.1

Найдите аппроксимирующую функцию i(U) в виде укороченного полинома 3-й степени i(u) = a₀ + a₁u + a₃u³, аналитически представляющую заданную в табл. 9.1. вольт-амперную характеристику I(U) с допустимой погрешностью аппроксимации _доп = 0,15I(U = 0) в интервале аппроксимации U_min  U  U_max, где U_min= –3 В, U_max= 0.

Таблица 9.1

U, В	–3,0	–2,5	–2,0	–1,5	–1,0	–0,5	0
I, мА	0,2	0,25	0,4	0,8	1,3	2,0	3,0

Решение

Рассчитаем допустимую погрешность аппроксимации _доп. Из заданной в табл. 9.1 вольт-амперной характеристики находим, что при U =  0 ток I = 3 мА, значит _доп = 0,153 = 0,45 мА.

Поскольку требуется найти три варьируемых параметра a₀, a₁, a₃, выбираем три узла интерполирования:

u₁ = –3 В; u₂ = –1 B; u₃ = 0 В. Из табл. 9.1 видно, что i(u₁) = 0,2 мА; i(u₂) = 1,3 мА; i(u₃) = 3 мА.

Составляем систему трех линейных уравнений вида f(x_k) = x_k):

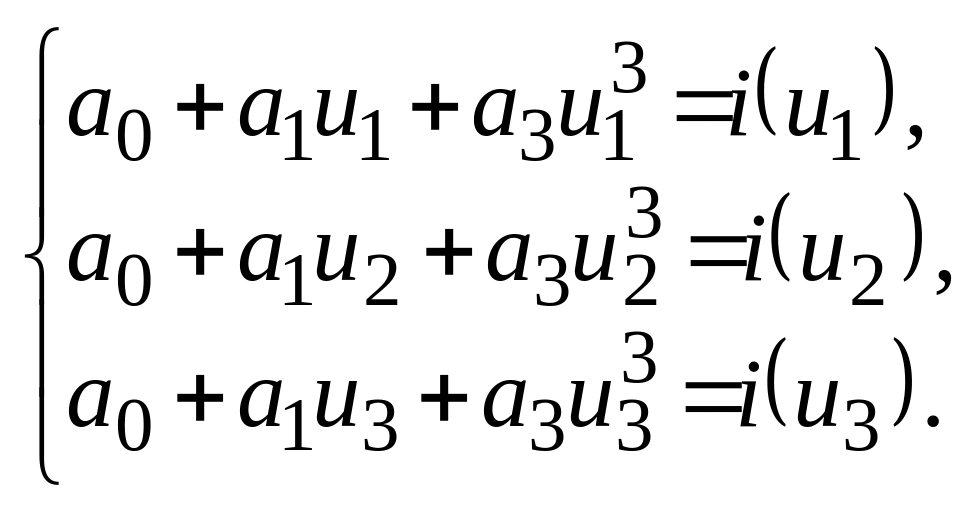
После подстановки соответствующих значений токов и напряжений получаем систему уравнений

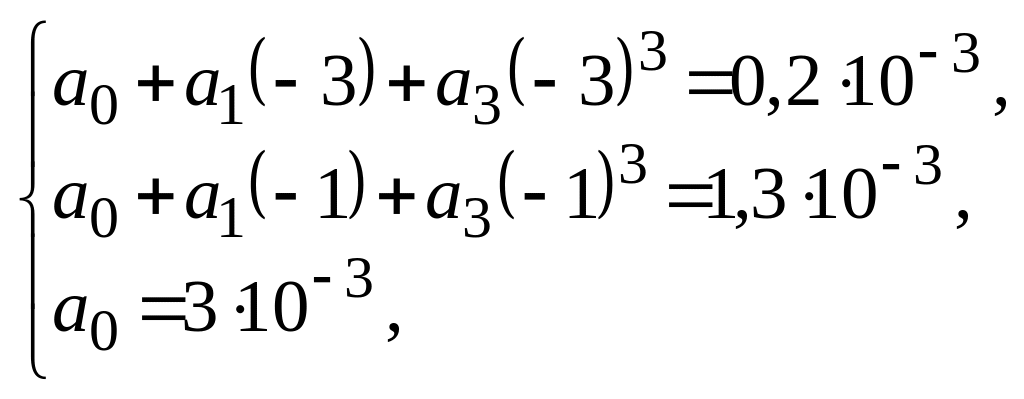
решая которую, находим

a₀ = 310^–3; а₁ = 1,79610^–3; a₃  = –0,09610^–3.

Аппроксимирующая функция i(u) имеет вид

i(u) = 310^–3 + 1,79610^–3u – 0,09610^–3u³.

Проверим точность аппроксимации, рассчитав i(и) при всех заданных значениях U. В табл. 9.2 приведены значения заданной вольт-амперной характеристики I(U), аппроксимирующей функции i(u) и погрешности аппроксимации  = i(u) –IU).

Таблица 9.2

U, В	–3	–2,5	– 2,0	–1,5	– 1, 0	–0,5	0
I(U), мА	0,2	0,25	0,4	0,8	1,3	2	3
i(u), мА	0,2	0,01	0,176	0,63	1,3	2,114	3
, мА	0	–0,24	–0,224	–0,17	0	0,114	0

Рис. 9.2

Как и следовало ожидать, в узлах интерполирования погрешность аппроксимации равна нулю, что подтверждает правильность решения составленной системы уравнений. Во всем интервале погрешность не превосходит допустимую величину _доп = 0,45 мА, что свидетельствует о правильности выбора вида аппроксимирующей функции и узлов интерполирования.

На рис. 9.2 приведены графики заданной вольт-ам­перной характеристики I(U), аппроксимирующей функции i(u) и погрешности аппроксимации .