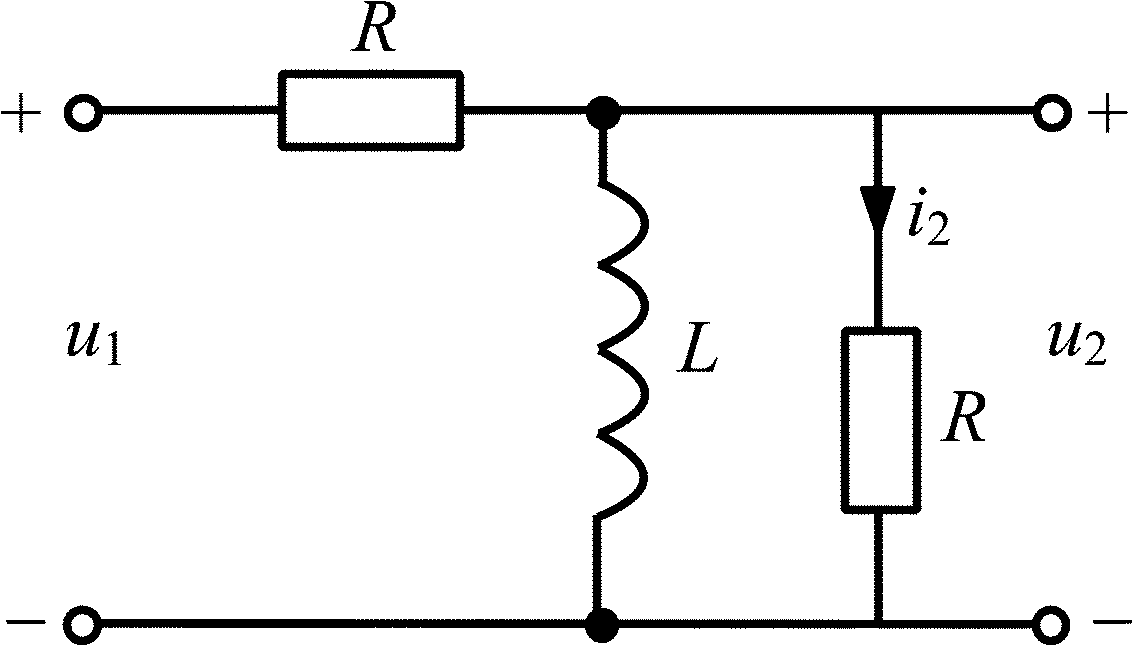
Пример 4.1

Найдите операторную передаточную функцию цепи, схема которой представлена на рис. 4.1.

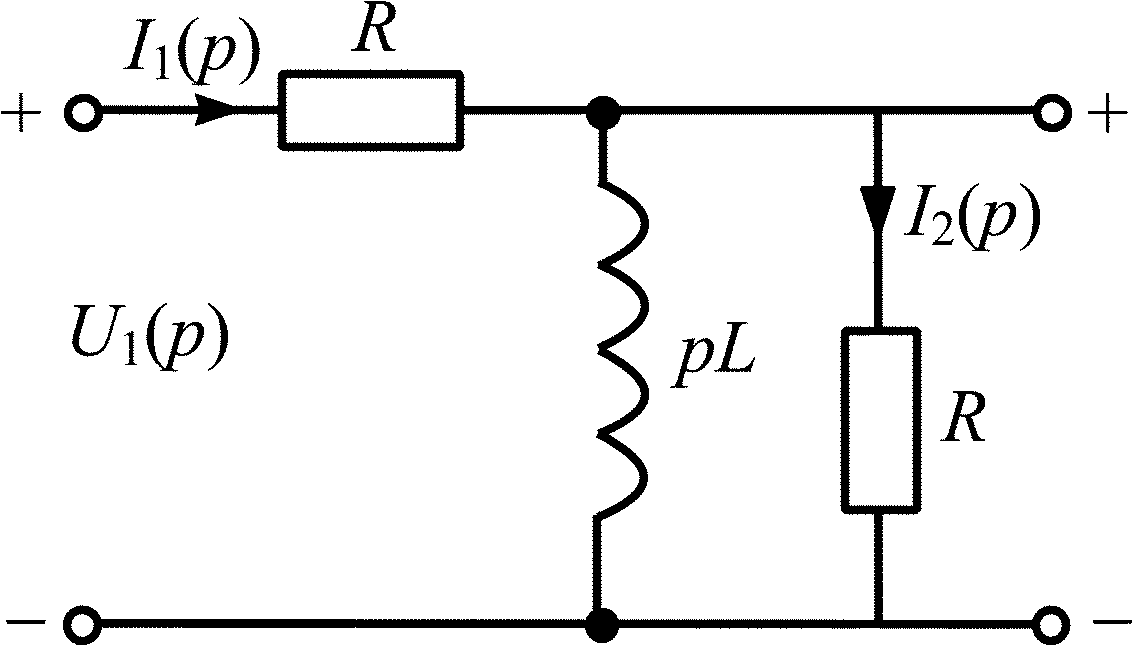
Рис. 4.1	Рис. 4.2

Решение

Нарисуем операторную схему замещения (рис. 4.2); начальные условия нулевые, поэтому операторная схема замещения цепи не имеет дополнительного источника.

Выразим I₂(p) и U₁(p) через I₁(p):

.

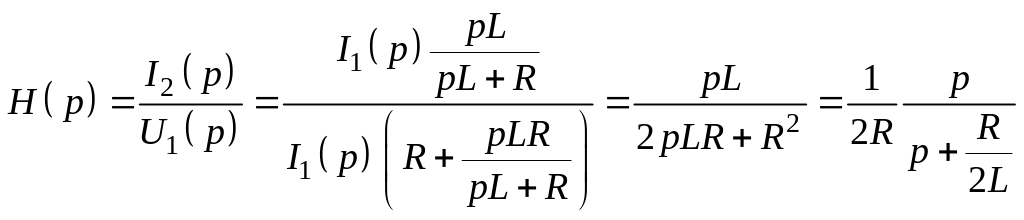Пример 4.2

Найдите операторную передаточную функцию цепи, схема которой представлена на рис. 4.3. Постройте графики АЧХ и ФЧХ цепи.

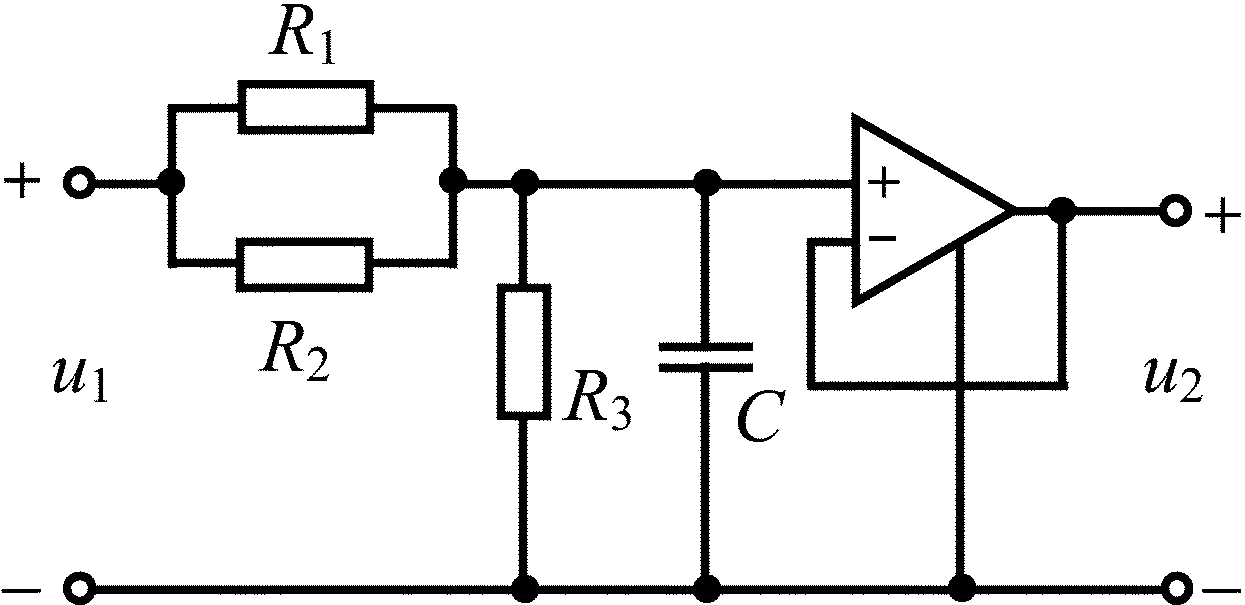
Рис. 4.3

Решение

При построении операторной схемы замещения заданной цепи (рис. 4.4) усилитель-повторитель напряжения заменен зависимым источником в виде ИНУН из табл. 1.6.

Выразим U₂(p) через U₁(p), используя метод узловых напряжений, который позволяет составить уравнение для узлового напряжения U₃(p):

U₃(p)(G₁ + G₂ + G₃ + pC) – U₁(p)(G₁ + G₂) = 0,

где .

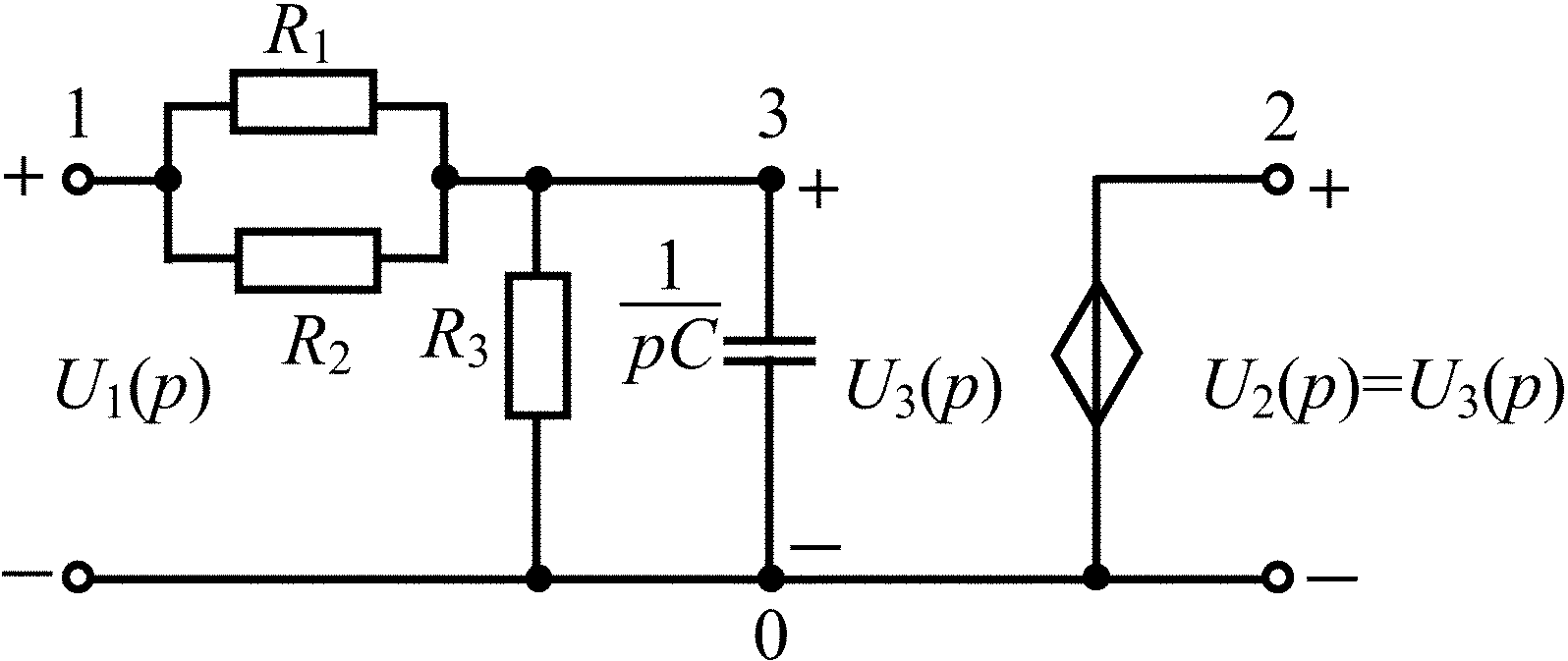
Рис. 4.4

Подставим в полученное уравнение вместо напряжения U₃(p), равное ему напряжение U₂(p). После преобразований получим

.

Найдем комплексную передаточную функцию, заменив p на j:

.

АЧХ цепи найдем как модуль H(j), равный отношению модулей ее числителя и знаменателя, ФЧХ – как разность аргументов числителя и знаменателя:

.

Примерные графики АЧХ и ФЧХ цепи приведены на рис. 4.5.

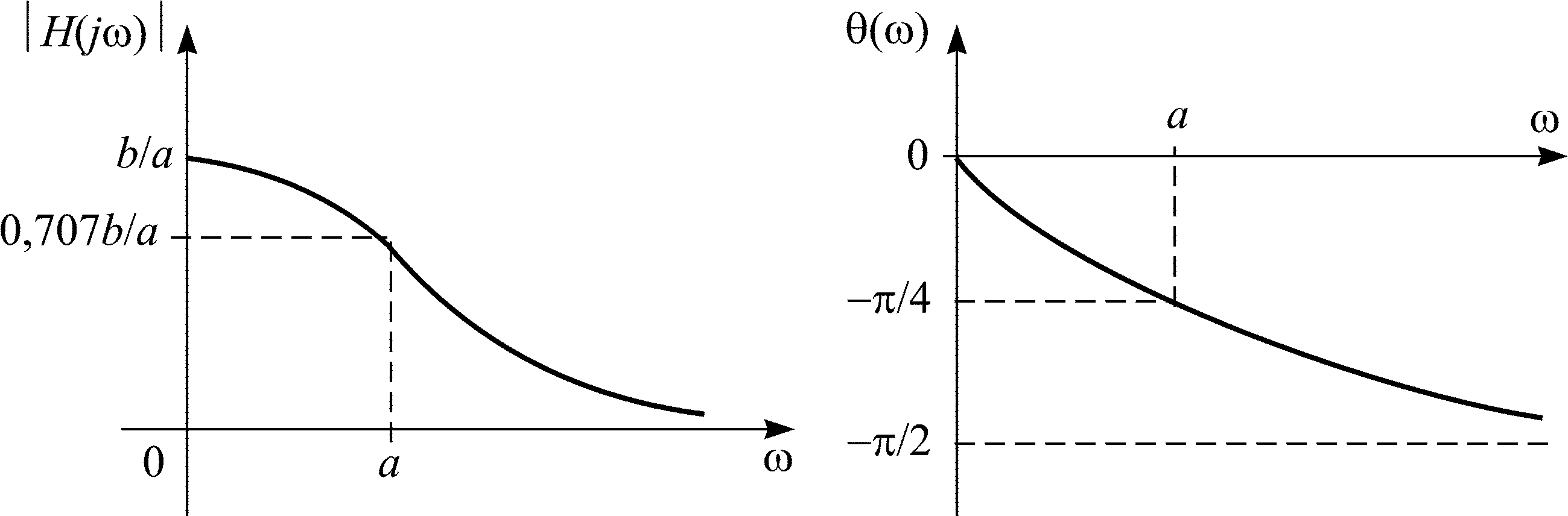
Рис. 4.5

Пример 4.3

Найдите операторную передаточную функцию цепи, схема которой представлена на рис. 4.6.

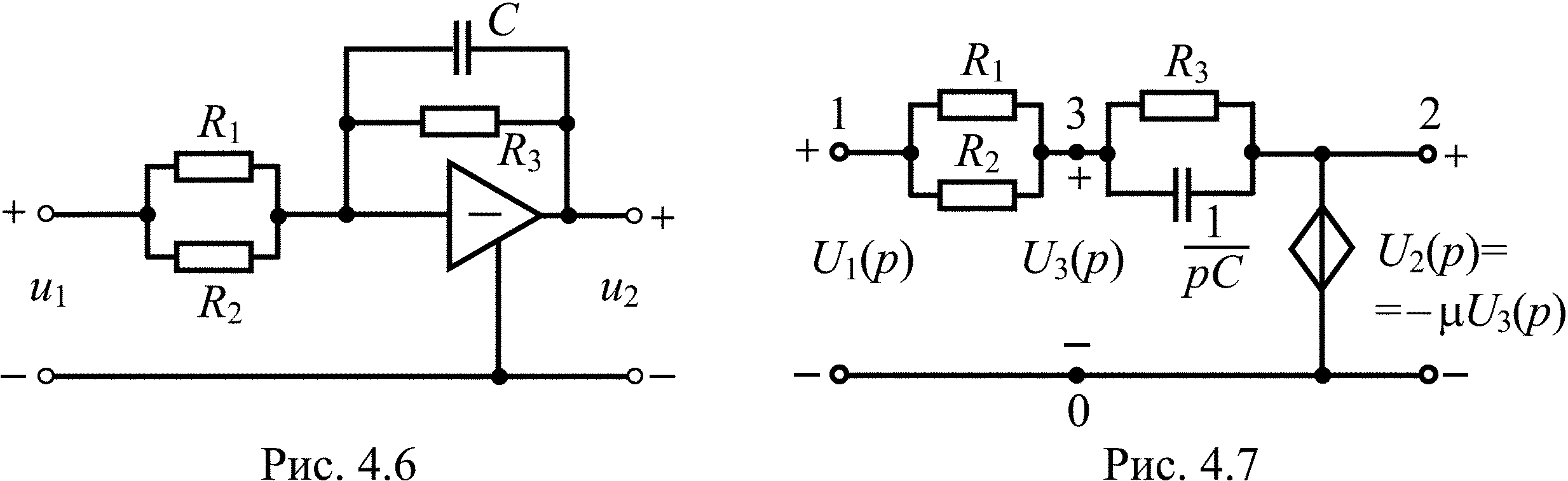
Решение

Схема замещения цепи показана на рис. 4.7. Запишем уравнение для узлового напряжения U₃(p):

U₃(p)(G₁ + G₂ + G₃ + pC) – U₁(p)(G₁ + G₂) – U₂(p)( G₃ + pC) = 0.

Считая операционный усилитель идеальным (  ), напряжением можно пренебречь, так как U₃(p) = 0.

После преобразований получим

.

Пример 4.4

Найдите операторную передаточную функцию цепи, схема которой представлена на рис. 4.8.

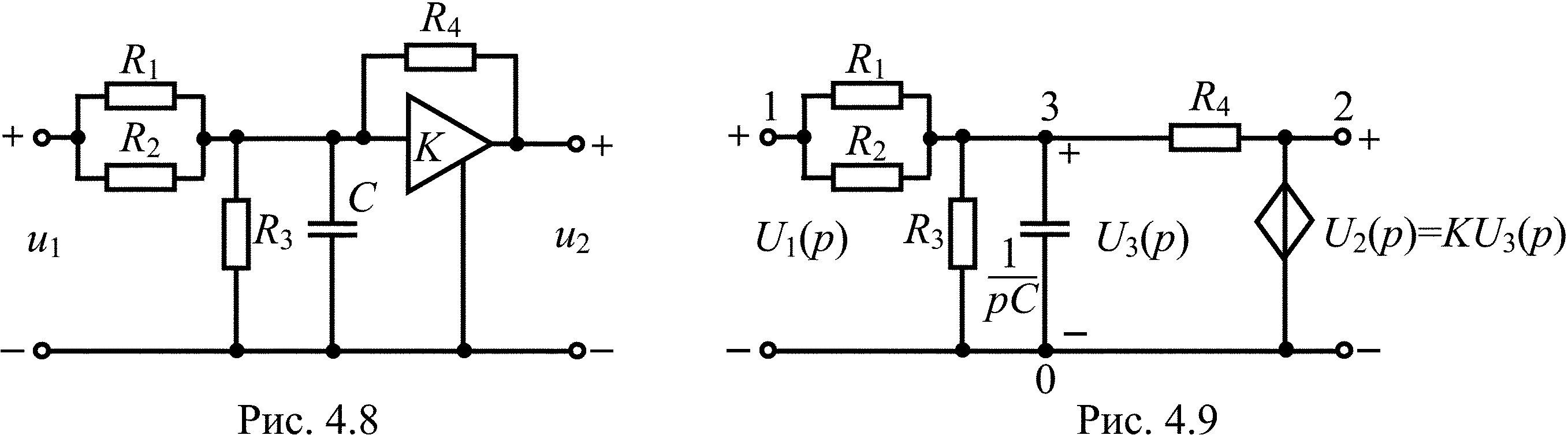
Ответ: Схема замещения цепи представлена на рис. 4.9.

.

4.2. Единичное импульсное воздействие. Импульсная характеристика цепи [1, с. 254–258, 260–261; 2, с. 200–204]

Импульсное воздействие – это однополярное воздействие любой формы, длительность которого значительно меньше времени, необходимого для сколько-нибудь заметного изменения свободных колебаний цепи. Для получения возможности сопоставления реакций электрических цепей на кратковременные однополярные воздействия вводится понятие типового импульсного воздействия, которое математически описывается единичной импульсной функцией (t), называемой также -функцией или функцией Дирака.

Значения этой функции бесконечно велики и знакопостоянны на бесконечно малом интервале времени, равны нулю вне этого интервала, а площадь, ограниченная графиком этой функции и осью абсцисс, равна единице, т. е.

если t₁  0 < t₂.

Импульсное воздействие на цепь описывается функцией S_и(t), где S_и – площадь импульса. Если S_и = 1, то воздействие называется единичным импульсом.

Отношение реакции электрической цепи на импульсное воздействие к «площади воздействия» при нулевых начальных условиях называется импульсной характеристикой цепи и обозначается g(t).

Если f₂(t) – реакция цепи на импульсное воздействие S_и(t), то

.

L-изображением импульсной характеристики цепи является операторная передаточная функция, т. е.

g(t)  H(p).

Если, например, , то g(t) = bе^–at.

Поскольку после окончания импульсного воздействия цепь переходит в режим свободных колебаний, а в устойчивых цепях свободные колебания убывают с течением времени, то условие может рассматриваться как одно из определений устойчивой электрической цепи.