3.5. Методы нахождения оригинала по изображению [1, с. 238–241; 2, с. 191–193]

В задачах анализа переходных колебаний в линейных электрических цепях с сосредоточенными параметрами изображение реакции F(p) является рациональной дробью с вещественными коэффициентами:

.

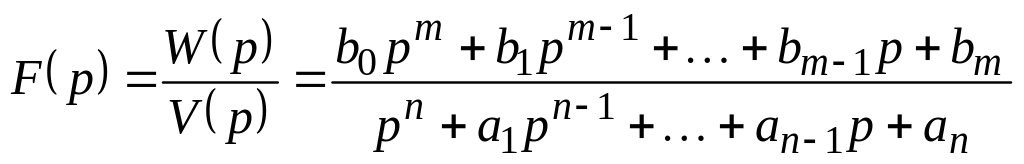Следует обратить внимание на то, что коэффициент при старшей степени p в знаменателе должен быть равен единице.

В простейших случаях оригинал может быть найден по таблицам соответствия, некоторые функции из которых приведены в табл. 3.1.

В общем случае, если m < n и знаменатель функции не имеет кратных (одинаковых) корней, используется теорема разложения, согласно которой для определения оригинала f(t) необходимо приравнять V(p) = 0, найти корни знаменателя p₁, p₂, …, p_n (полюсы функции F(p)) и разложить F(p) на сумму простых дробей:

.

Коэффициенты разложения A₁, A₂, …A_n называются вычетами функции F(p) в соответствующих полюсах и могут быть найдены по формуле

.

Следует заметить, что вычеты в вещественных полюсах будут вещественными, а вычеты в комплексно-сопряженных полюсах  – комплексно-сопряженными величинами.

Оригинал функции F(p) окажется равным

.

В некоторых задачах анализа переходных колебаний изображение реакции F(p) может представлять собой дробно-рациональную функцию с вещественными коэффициентами, у которой степени числителя и знаменателя равны (m = n).

В этом случае разложение F(p) на сумму простых дробей будет иметь вид

,

а оригинал окажется равным

.

Пример 3.1

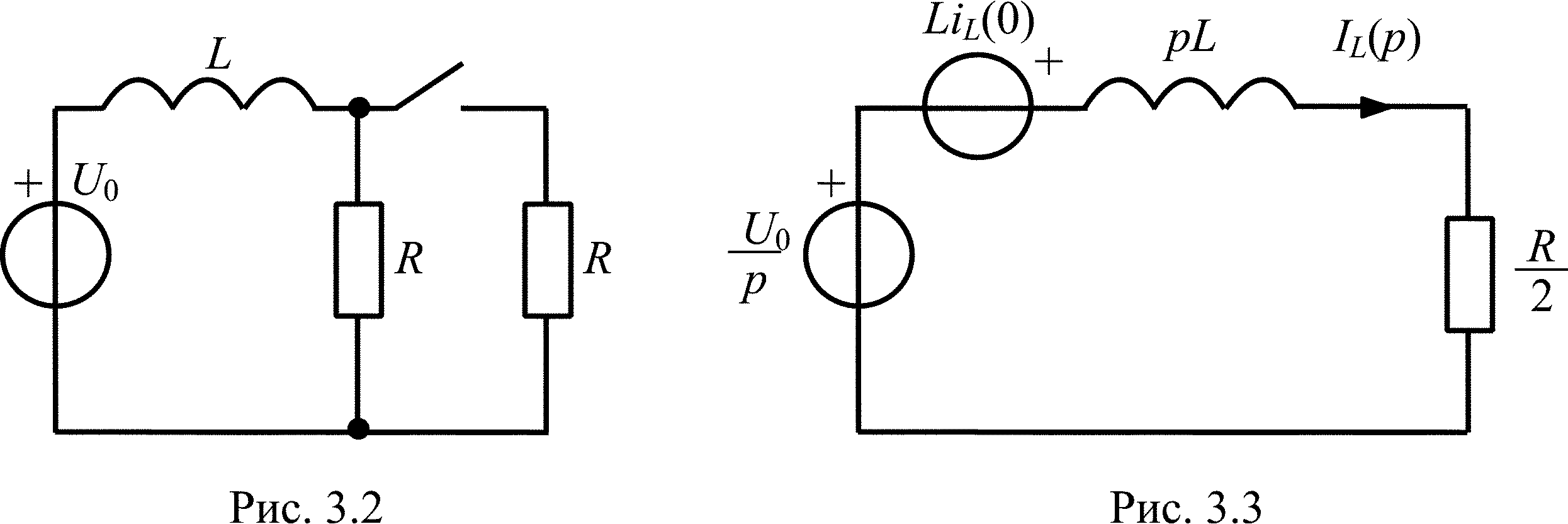
В цепи, схема которой приведена на рис. 3.2, в момент времени t = 0 замыкается ключ. Найдите закон изменения тока через индуктивность после коммутации, если U₀ = 10 В, L = 1 Гн, R = 10 Ом. Решить задачу операторным методом.

Решение

По закону коммутации i_L(0_–) = i_L(0₊) = U₀/R = 1 А. Нарисуем операторную схему замещения цепи для t > 0 (ключ замкнут) с учетом начального запаса энергии в индуктивности (рис. 3.3). Изображение тока в этой цепи определяется по закону Ома

.

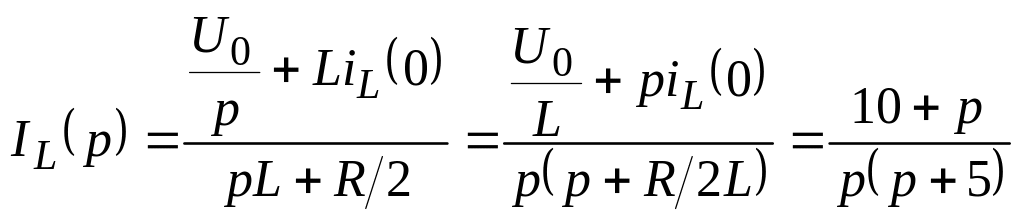Для нахождения оригинала воспользуемся теоремой разложения:

.

Тогда

.

Этому изображению соответствует оригинал

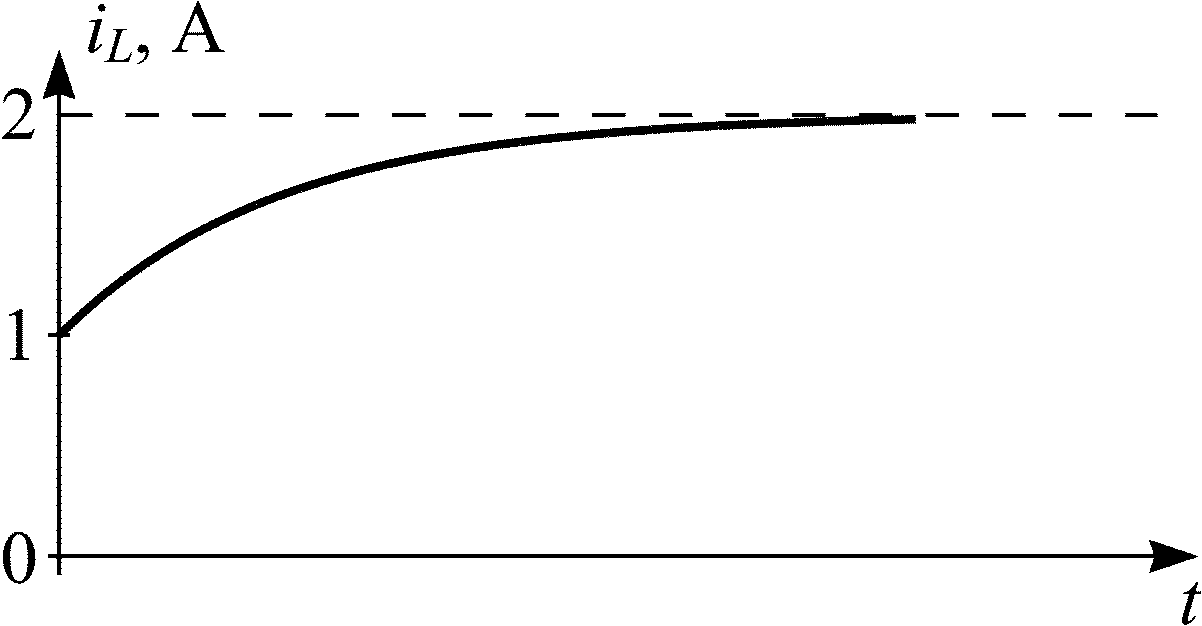
i_L(t) = 2 – e^–5t, А.

Проверка:

i_L(0) = 2 – 1 = 1 А; i_L() = 2 А.

Рис. 3.4

Первое значение соответствует начальным условиям задачи, второе равно установившемуся значению постоянного тока в цепи с замкнутым ключом.

На рис. 3.4 показан примерный график тока через индуктив­ность.

Контрольные вопросы

1. Какие функции преобразуемы по Лапласу?

2. Сформулируйте основные свойства преобразования Лапласа.

3. Чему равны операторные сопротивления индуктивности, емкости, резистивного сопротивления?

4. Какие законы электрической цепи справедливы для L-изобра­жений колебаний?

5. Как учитывается начальный запас энергии в индуктивности и емкости при составлении операторной схемы замещения цепи?

6. Каков порядок анализа переходных колебаний в цепи операторным методом?

7. Каков порядок нахождения оригинала по его L-изображению с помощью теоремы разложения?

4. Методические рекомендации к выполнению задачи 3

4.1. Операторная передаточная функция устойчивой цепи [1, c. 243–246; 2, c. 196–198]

Под операторной передаточной функцией H(p) понимают отношение L-изображения реакции цепи к L-изображению воздействия, подведенного к цепи, при нулевых начальных условиях задачи. Воздействием на цепь может быть задающее напряжение или задающий ток источника, реакцией – любой ток или напряжение в цепи.

В соответствии с этим возможны следующие виды передаточных функций:

Операторная передаточная функция представляет собой дробную рациональную функцию с вещественными коэффициентами

,

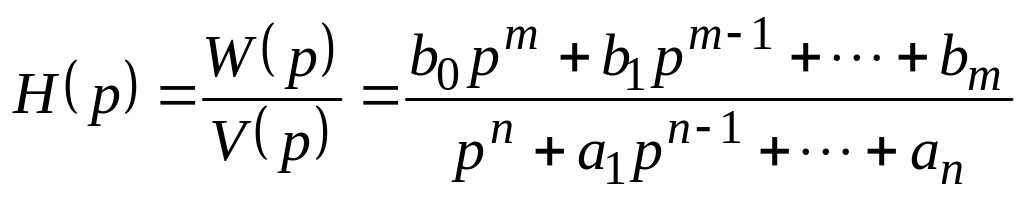степень числителя которой обычно не превышает степени знаменателя, т. е. m  n.

Цепь устойчива, если свободные колебания в ней неограниченно убывают при t  . Полюсы передаточной функции устойчивой цепи (корни полинома знаменателя V(p)) располагаются в левой полуплоскости комплексной переменной p.

Полином с вещественными коэффициентами, имеющий корни только в левой полуплоскости, называется полиномом Гурвица. Таким образом, передаточная функция устойчивой цепи имеет в знаменателе полином Гурвица.

Комплексная передаточная функция может быть получена из операторной заменой p = j. При этом модуль комплексной передаточной функции |H(j| представляет собой амплитудно-частотную характеристику цепи, а аргумент () – ее фазочастотную характеристику.

Рассмотрим несколько примеров определения операторной передаточной функции H(p) пассивной и активной цепей.