Лабораторная работа №8
Функции пользователя
1. Цель работы
Целью лабораторной работы является получение практических навыков в работе с функциями пользователя и передачей параметров функциям.
2. Темы для предварительной проработки
Указатели и массивы.
Функции пользователя.
3. Задания для выполнения
Составить программу, которая решает задачу для лабораторной работы №5 с такими дополнительными условиями:
размерность матрицы должна вводиться при выполнении программы;
само решение задачи должно быть оформлено в виде функции, которой передается матрица и ее размерность.
4. Варианты индивидуальных заданий
-
№ варианта
Содержание задания
Иллюстрация
1
Заполнить матрицу случайными числами. Развернуть матрицу на 90o по часовой стрелке.

2
Заполнить матрицу случайными числами. Отобразить матрицу симметрично относительно главной диагонали

3
Заполнить матрицу ЛП, от левого верхнего угла по спирали: вправо - вниз - влево - вверх.

4
Заполнить матрицу ЛП, от центра по спирали: влево - вниз - вправо - ввер
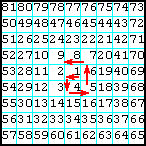
5
Заполнить матрицу случайными числами. На главной диагонали разместить суммы элементов, которые лежат на той же строке и том же столбце.

6
Заполнить матрицу ЛП, от левого верхнего угла по диагонали: вправо - вверх.
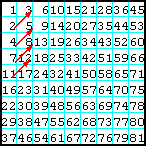
7
Заполнить секторы матрицы, которые лежат влево и вправо от главной и побочной диагоналей, ЛП, от левого верхнего угла вниз - вправо. Остаток матрицы заполнить нулями.

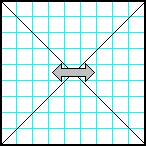
8
Заполнить матрицу случайными числами. Отобразить симметрично относительно вертикальной оси секторы матрицы, которые лежат влево и вправо от главной и побочной диагоналей.
9
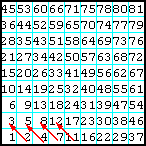
9 Заполнить матрицу ЛП, от левого нижнего угла по диагонали: влево - вверх
10
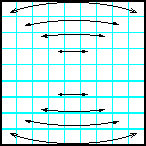
Заполнить матрицу случайными числами. Отобразить главную и побочную диагонали симметрично относительно вертикальной оси.
11
Заполнить матрицу случайными числами. Разместить на главной диагонали суммы элементов, которые лежат на диагоналях, перпендикулярных к главной

12
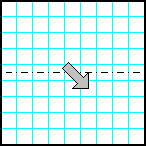
Заполнить матрицу случайными числами. Отобразить верхнюю половину матрицы на нижнюю зеркально симметрично относительно горизонтальной оси.
13
Заполнить матрицу случайными числами. Розбити матрицу на квадраты размером 3х3. В центре каждого квадрата поместить сумму остальных элементов квадрата.
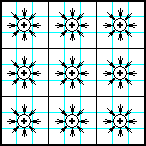
14
Заполнить матрицу случайными числами. Отобразить правую половину матрицы на левую зеркально симметрично относительно вертикальной оси.

15
Заполнить секторы матрицы, которые лежат влево и вправо от главной и побочной диагоналей ЛП, от левого верхнего угла вправо - вниз. Остаток матрицы заполнить нулями.
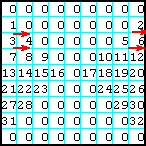
16
Заполнить матрицу случайными числами. Развернуть матрицу на 90o против часовой стрелки.
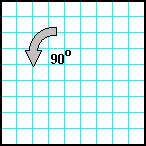
17
Заполнить матрицу случайными числами. Отобразить матрицу симметрично относительно побочной диагонали

18
Заполнить матрицу ЛП, от левого верхнего угла по спирали: вниз - вправо - вверх - влево.

19
Заполнить секторы матрицы, которые лежат выше и ниже главной и побочной диагоналей, ЛП, от левого верхнего угла вниз - вправо. Остаток матрицы заполнить нулями.

5. Пример решения задачи (вариант 30)
Решение приводится со ссылками на работу №5.
5.1. Разработка алгоритма решения.
Сам алгоритм решения мог бы быть тем же, что и в работе №5. Но обратим внимание на то, что условие этой работы несколько отлично от условия работы №5. Если в работе №5 мы имели фиксированную размерность матрицы, то тут у нас размерность матрицы заранее не известна. Составляет ли это существенное различие? Да. Если мы проверим функционирования алгоритма работы №5 при разных значениях размерности (S), то мы убедимся, что корректно он срабатывает только при нечетных значениях S. При четных значениях верхняя половина матрицы формируется правильно, а в нижней половине область ненулевых значений будет захватывать также и сами диагонали, что не соответствует условиям задания. Поэтому для этой работы следует пересмотреть алгоритм.
Для элемента, который лежит на главной диагонали, индексы удовлетворяют условию: L=R, на побочной - R=S-L-1. Следовательно, для верхней половины условие попадания в ненулевую область: L < R < S-L-1, а для нижней: S-L-1 < R < L. Или, обобщая: min(L,S-L-1) < R < max(L,S-L-1) . В схеме алгоритма, которая приведена на рисунке 1, мы используем именно это условие. К тому же в схеме отражено разделение программы на две функции: главную функцию - main(), которая выполняет выделения памяти для матрицы, вызов функции заполнения матрицы и вывод результата, и функцию fill(), которая выполняет заполнение матрицы по заданным правилам.
|
Рисунок 1. Схема алгоритма |
В этой работе ми несколько усложним алгоритм, добавив в него проверку значения S, которое введено оператором (блоки 3 - 8). Нижняя граница для значения S - 1, поскольку матрица нулевой или отрицательной размерности просто не имеет смысла. Верхняя граница - 24, поскольку для матрицы большего размера невозможно будет обеспечить наглядный вывод (она не поместится на экране).
5.2. Представление матрицы в памяти
Если в работе №5 было возможно представлять матрицу в программе как двумерный массив - естественное представление матрицы, то при условии динамического размещения в памяти ее представление уже не такое простое. Возможны три варианта размещения в памяти и представления матрицы в программе. Во всех трех вариантах очевидно, что общий объем памяти для размещения данных матрицы должен быть S2 элементов типа int.
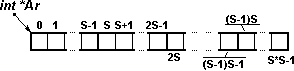
Вариант 1 показан на рис.2
|
Рисунок 2. Размещение в памяти. Вариант 1. |
Для данных матрицы выделяется необходимый объем памяти. В программе объявляется указатель на начало этой области. Тип этого указателя - int*. Таким образом, матрица является одномерным массивом и для того, чтобы по номеру строки (L) и столбца (R) определить индекс в одномерном массиве (N) следует выполнить вычисление: N=L*S+R.
Вариант 2 показан на рис.3.
|
Рисунок 3. Размещение в памяти. Вариант 2. |
Память для данных матрицы выделяется так же, как и в предыдущем случае. Но дополнительно выделяется память для одномерного массива размерности S, элементы которого имеют тип int* (указатель на целое). Указатель на начало этого массива имеет тип int** (указатель на указатель на целое). В элементы этого массива записываются указатели на начала соответствующих строк в массиве данных матрицы. В этом варианте можно обращаться к данным матрицы, указывая номера строки и столбца как два индекса в массиве указателей.
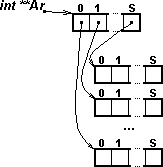
Вариант 3 показан на рис.4.
|
Рисунок 4. Размещение в памяти. Вариант 3 |
|
Этот вариант отличается от предыдущего тем, что для каждой строки матрицы память выделяется отдельно (S областей памяти по S элементов в каждой), и в массив указателей заносятся указатели на соответствующие области. Таким образом, матрица необязательно занимает смежные области памяти. Можно обращаться к данным матрицы, указывая два индекса. Выделение памяти (и соответственно - освобождение) нужно выполнять в цикле. Вариант 1 обеспечивает экономию памяти, а варианты 2 и 3 - возможность "естественного" обращения к элементам матрицы. Вариант 3 позволяет рациональнее использовать память, чем вариант 2, но вариант 2 алгоритмически более простой. Мы покажем реализации алгоритма для вариантов 1 и 3.