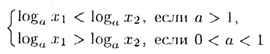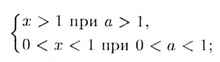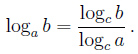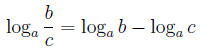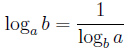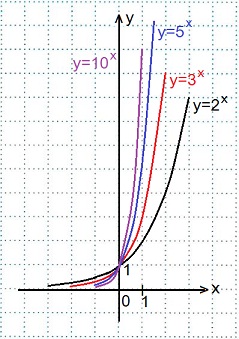
3) В одной координатной плоскости построить графики функций:

y=2^x, y=3^x, y=5^x, y=10^x. Сделать выводы.

График функции у=2^х мы уже строили, графики остальных функций строим аналогично, причем, достаточно будет найти значения функций при х=0 и при х=±1.

Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля  (E (y)=R₊).

Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю. Чем больше основание а (если a>1) показательной функции у=а^х, тем ближе расположена кривая к оси Оу.

Все  данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.

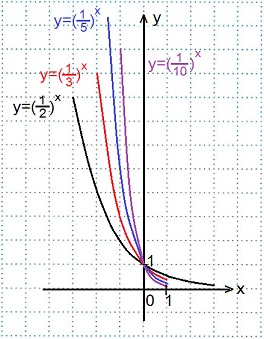
4) В одной координатной плоскости построить графики функций:

y=(¹/₂)^x, y=(¹/₃)^x, y=(¹/₅)^x, y=(¹/₁₀)^x. Сделать выводы.

Смотрите построение графика функции y=(¹/₂)^x выше, графики остальных функций строим аналогично, вычислив их значения при х=0 и при х=±1.

Переменная х может принимать любое значение: D (y)=R, при этом область значений функции: E (y)=R₊.

Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю.

Чем меньше основание а (при 0<a<1) показательной функции у=а^х, тем ближе расположена кривая к оси Оу.

Все  эти функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.

Решить графически уравнения:

1) 3^x=4-x.

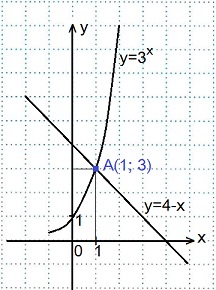В одной координатной плоскости построим графики функций: у=3^х и у=4-х.

 Графики пересеклись в точке А(1; 3).

 Ответ: 1.

 2) 0,5^х=х+3.

 

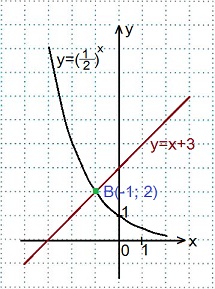
В одной координатной плоскости строим графики функций: у=0,5^х

(y=(¹/₂)^x )

 и у=х+3.

Графики пересеклись в точке В(-1; 2).

Ответ: -1.

 Найти область значений функции: 1) y=-2^x; 2) y=(¹/₃)^x+1; 3) y=3^x+1-5.

Решение.

 1) y=-2^x 

Область значений показательной функции y=2^x – все положительные числа, т.е.

0<2^x<+∞. Значит, умножая каждую часть двойного неравенства на (-1), получаем:

— ∞<-2^x<0.

Ответ: Е(у)=(-∞; 0).

 2) y=(¹/₃)^x+1;

0<(¹/₃)^x<+∞, тогда, прибавляя ко всем частям двойного неравенства число 1, получаем:

0+1<(¹/₃)^x+1<+∞+1;

1<(¹/₃)^x+1<+∞.

Ответ: Е(у)=(1; +∞).

 3) y=3^x+1-5.

Запишем функцию в виде: у=3^х∙3-5.

0<3^x<+∞;   умножаем все части двойного неравенства на 3:

0∙3<3^x∙3<(+∞)∙3;

0<3^x∙3<+∞;  из всех частей двойного неравенства вычитаем 5:

0-5<3^x∙3-5<+∞-5;

— 5<3^x∙3-5<+∞.

Ответ: Е(у)=(-5; +∞).

Билет 9.

Логарифмическая функция, ее свойства и график

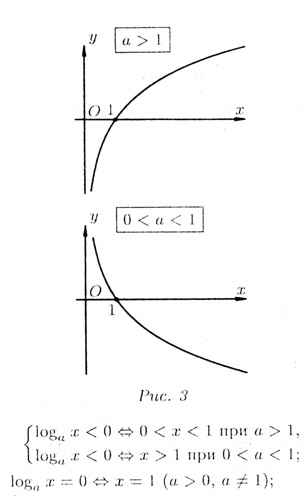
Логарифмическая функция у = loga x (а > 0, a # 1 ) определена только при х > 0 (у = loga x <=> х = аy) и обладает следующими свойствами: 1. монотонности: 0 < x1 < x2<=> 2. сохранения знака:у = loga x > 0 <=> 3. асимптотического стремления к бесконечности: при х —> 0 (x > 0), Прямая х = 0 называется вертикальной асимптотой графика функции у = loga x.

Билет 10. Определение логарифма числа. Основное логарифмическое тождество. Логарифм произведения. Логарифм положительного числа   по основанию   (обозначается  ) — это показатель степени, в которую надо возвести  , чтобы получить  . b > 0, a > 0, а≠ 1.

,

Пример:

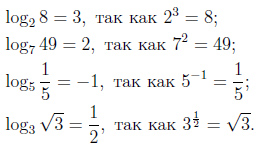
Десятичный логарифм — логарифм с основанием 10, который обозначается как  .

,  , так как 

Натуральный логарифм — логарифм с основанием  , обозначается 

Основное логарифмическое тождество

Логарифм произведения — это сумма логарифмов

Билет 11. Свойства логарифмов. Логарифм частного, логарифм степени.

Логарифм частного — это разность логарифмов

Свойства степени логарифмируемого числа и основания логарифма

Показатель степени логарифмируемого числа 

Показатель степени основания логарифма

, в частности если m = n, мы получаем формулу: , например:

Переход к новому основанию

, частности, если c = b, то  , и тогда:

Билет 12. Десятичные и натуральные логарифмы. Переход от одного основания логарифма к другому.

Десятичный логарифм — логарифм с основанием 10, который обозначается как  .

,  , так как 

Натуральный логарифм — логарифм с основанием  , обозначается 

Свойства степени логарифмируемого числа и основания логарифма

Показатель степени логарифмируемого числа 

Показатель степени основания логарифма

, в частности если m = n, мы получаем формулу: , например:

Переход к новому основанию

, частности, если c = b, то  , и тогда:

Билет 13. Показательные уравнения. Способы их решения.

Показательными уравнениями называются уравнения, содержащие неизвестную величину в показателе степени.

К таким относятся, например, уравнения 3^x = 2^x—1 ,   и другие.

Показательные уравнения, так же как и тригонометрические, в отличие от алгебраических (например, линейных, квадратных), относятся к трансцендентным уравнениям.

Простейшим  показательным   уравнением  является  уравнение

а^x = b,                                           (1)

где а и b — данные положительные числа (a =/= 1), a x — неизвестная величина. Такое уравнение имеет единственный  корень х = log_а b. Более сложные показательные уравнения часто сводятся либо к алгебраическим уравнениям, либо к уравнениям вида   (1).

Рассмотрим основные способы решения показательных уравнений на частных примерах.

1. Решить уравнение

5^x—6 = 5^{15 —2x},

Решение подобных уравнений основано на следующем свойстве степеней: если две степени одного и того же положительного числа, отличного от 1, равны, то равны и их показатели. В данном случае это свойство степеней дает:

х — 6 = 15 — 2х,

откуда х = 7.

Проверка. При х = 7    5^x—6 = 5,   5^{15 —2x} = 5. Значит, х = 7 — корень данного уравнения.

Ответ    х = 7.

Аналогично решается уравнение

Действительно, 

Поэтому 

откуда 2х = — х², или x₁  = 0,  x₂  = — 2. Проверка показывает, что оба эти значения худовлетворяют данному уравнению.

Ответ.  x₁  = 0,  x₂  = — 2.

По этому же принципу можно решать и показательное уравнение а^x = b, если b есть целая степень числа а. Например, если 3^x = 27, то, представив 27 в виде 27 = 3³, получаем 3^x = 3³, откуда х = 3.

II. Иногда путем введения новой неизвестной величины показательное уравнение сводится к алгебраическому уравнению. Пусть, например, нужно решить уравнение

4^x + 2^x — 6 = 0.

Обозначим 2^x через у. Тогда 4^x = (2²)^x = 2^2x = (2^x)² = у². Поэтому данное уравнение сводится к квадратному уравнению

у² + у — 6  = 0,

из которого получаем: у₁ = 2, у₂ = — 3. Но у = 2^x. Значит, если только данное уравнение имеет корни, то они должны удовлетворять либо уравнению 2^x = 2, либо уравнению 2^x = —3. Первое из этих уравнений имеет корень х = 1; второе же  уравнение корней не имеет, поскольку выражение 2^x не может принимать отрицательных значений. Итак, мы получили: х = 1.

Проверка.  При х = 1

4^x + 2^x — 6 = 4¹ + 2¹ — 6 =  0.

Следовательно, х = 1 — корень данного уравнения.

Ответ.  х = 1.

III. Решить уравнение

2^x = 3^x.

Разделив обе части данного уравнения   на 3^x (такое  деление возможно, поскольку при любом х   3^x > 0), получим: (²/₃)^x = 1.

Но 1 = (²/₃)⁰, поэтому х = 0.  Проверка  показывает, что это действительно корень данного уравнения.

Ответ,   х = 0.

Аналогично решается уравнение 5^2x = 7^3x.

Действительно,    5^2x= (5²)^x =25^x;    7^3x = (7³)^x = 343^x. Поэтому данное уравнение можно переписать в виде

25^x = 343^x.

Отсюда, так же как и в, предыдущем случае, получаем: х = 0.

Билет 14. Логарифмические уравнения. Способы их решения.