Понятие обратной функции

    Если функция задана уравнением вида f (x, y) = 0, не разрешенным относительно у, то она при некоторых условиях называется неявной функцией аргумента x.    Пусть задана некоторая функция у = f(х), которая каждому элементу из множества D (f) ставится в соответствие один элемент из множества Е ( f ). Если обратное соответствие есть тоже функция, то есть, каждому значению у   E( f ) соответствует единственное значение х   D ( f ), то ее называют обратной функцией по отношению к функции f (х).    В этом случае соотношение у = f (х) определяет х как неявную функцию от у. Если это соотношение разрешимо относительно х, то получим явное выражение обратной функции: х = g (у).   Если функция g является обратной по отношению к функции f, то и функция f является обратной по отношению к функции g, т. е. эти две функции - взаимно-обратные.   Одна и та же кривая у = f (х) представляет собой график функции у = f (х) и график обратной функции х = g (у) (если она существует), но в последнем случае значения аргумента рассматриваются на оси Оу, а значения функции - на оси Ох.   Если придерживаться стандартных обозначений и независимую переменную обозначать через х, а функцию − через у, то функция, обратная по отношению к у = f (х), запишется в виде у = g (х). В этом случае график функции у = g (х) симметричен графику функции у = f (х) относительно прямой у = х − биссектрисы I и III координатных углов.   Для взаимно - обратных функций имеют место следующие соотношения

D ( f ) = E ( g ), E ( f )= D (g),

т. е. область определения данной функции совпадает с множеством значений обратной функции, и наоборот.

Основные элементарные функции

  Линейная функция подробно рассматривалась в разделе "Аналитическая геометрия".   Степенная функция определяется соотношением y = xⁿ, n ≠ 0 . При натуральных значениях n эта функция определена на всей числовой прямой, т. е.х   R. При четном показателе степени степенная функция является четной и y принимает положительные значения. Ее графиками служат параболы соответственно второго, четвертого и т.д. порядков, рис. 5.4.    При нечетном показателе функция является нечетной и принимает значения y   (− ∞, + ∞) . Ее графиками служат параболы третьего, пятого и т. д. порядков,рис. 5.5.    П о к а з а т е л ь н а я функция y = a^x, (a ≠ 1, a > 0). Область ее определения x   (- ∞, + ∞), множество значений y   ( 0, + ∞). Если a > 1, то функция монотонно возрастает, а если 0 < a < 1 - монотонно убывает. При этом для любого основания выполняется равенство a⁰ = 1. Следовательно, график любой показательной функции проходит через точку (0; 1), рис. 5.6.    Л о г а р и ф м и ч е с к а я функция. Эта функция является обратной по отношению к показательной. График логарифмической функции симметричен графику показательной функции относительно прямой у = х. При этом для любого основания а > 0 и а ≠ 1 выполняется условие log_a1 = 0, поэтому график всякой логарифмической функции проходит через точку (1; 0), рис. 5.7.    Тригонометрические функции y = sin x, y = cos x, y = tg x, y = ctg x. Функции y = sin х и у = cos х определены на всей числовой прямой и имеют множеством значений промежуток [− 1, 1], рис. 5.8.   Функция у = tg х определена при всех значениях  , монотонно возрастает в каждом интервале области определения.     Функция у = ctg х определена при всех значениях x ≠ π n, n   N, и монотонно убывает в каждом интервале области определения.    Множеством значений тангенса и котангенса служит промежуток (− ∞; + ∞).   Функции у = sin х, у = tg х и у = ctg х − нечетные, их графики симметричны относительно начала координат. Функция у = cos x - четная, ее график симметричен относительно оси Оу.   Тригонометрические функции являются периодическими.    Определение. Функция f (х) называется периодической, если существует такое число Т > 0, что для любых значений аргумента из области определения функции имеет место равенство f (x ± T) = f (x).   Основной период функций у = sin х и у = cos x равен 2·p, основной период функций у = tg x и y = ctg x равен p.   Обратные тригонометрические функции. Функция y = arcsin x , где х   [− 1; + 1], y   [− p/ 2, p/2 ], означает, что у есть угол из промежутка [− p/ 2, p/2 ], синус которого равен х, то есть х = sin у.     Функция y = arcsin x является обратной для функции y = sin x, x  [− p/ 2, p/ 2 ], у   [− 1; + 1], рис. 5.9.   Функция у = arcсos х, x   [− 1, 1], y   [0, p] обратная функции у = сos х, где х   [0, p] и y   [− 1, 1]. Её график симметричен графику у = сos х относительно прямой у = х, рис. 5.10.    Функция у = arctg x, где x   (− ∞; + ∞) и y   (− p/ 2, p/ 2 ), является обратной функции y = tg x, y   (− ∞; + ∞) и . Ее график симметричен графику функции y = tgx, x   (− p/ 2, p/ 2 ), относительно прямой у = х, рис. 5.11.   Функция у = arcctg x, x   (− ∞; + ∞), y   (0; p) обратная функции у = ctg x, x   (0; p), у   (− ∞; + ∞). Ее график симметричен графику у = ctg x, x   (0; p), относительно прямой у = х, 

Билет 7.

Степень с действительным показателем Пусть дано положительное число   и произвольное действительное число  . Число  называется степенью, число   — основанием степени, число   — показателем степени. По определению полагают: . . ,  . Если   и   — положительные числа,   и   — любые действительные числа, то справедливы следующие свойства: . . . . . .

• Билет 8. Показательная функция, её график и свойства.Функцию вида y=a^x, где а>0, a≠1, х – любое число, называют показательной функцией.

• Область определения показательной функции: D (y)=R – множество всех действительных чисел.

• Область значений показательной функции: E (y)=R₊ - множество всех положительных чисел.

• Показательная функция  y=a^x возрастает при a>1.

• Показательная функция y=a^x убывает при 0<a<1.

Справедливы все свойства степенной функции:

• а⁰=1  Любое число (кроме нуля) в нулевой степени равно единице.

•  а¹=а  Любое число в первой степени равно самому себе.

•  a^x∙a^y=a^x+y   При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.

•  a^x:a^y=a^x- y  При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

• (a^x)^y=a^xy   При возведении степени в степень основание оставляют прежним, а показатели перемножают

•  (a∙b)^x=a^x∙b^y   При возведении произведения в степень возводят в эту степень каждый из множителей.

• (a/b)^x=a^x/b^y  При возведении дроби в степень возводят в эту степень и числитель и знаменатель дроби.

•   а^-х=1/a^x

•  (a/b)^-x=(b/a)^x.

Примеры.

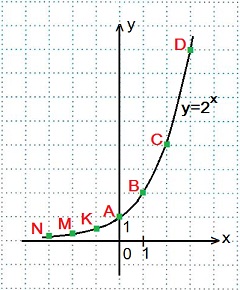
1) Построить график функции y=2^x. Найдем значения функции

при х=0, х=±1, х=±2, х=±3.

x=0, y=2⁰=1;                   Точка А.

x=1, y=2¹=2;                   Точка В.

x=2, y=2²=4;                   Точка С.

x=3, y=2³=8;                   Точка D.              

x=-1, y=2^-1=¹/₂=0,5;       Точка K.

x=-2, y=2^-2=¹/₄=0,25;     Точка M.

x=-3, y=2^-3=¹/₈=0,125;   Точка N.

Большему  значению аргумента х соответствует и большее значение функции у. Функция y=2^x возрастает на всей области определения D (y)=R, так как основание функции 2>1.

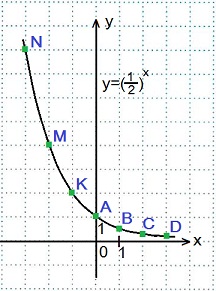
2) Построить график функции y=(¹/₂)^x. Найдем значения функции

при х=0, х=±1, х=±2, х=±3.

x=0, y=(½)⁰=1;                  Точка A.

x=1, y=(½)¹=½=0,5;          Точка B.

x=2, y=(½)²=¼=0,25;        Точка C.

x=3, y=(½)³=1/8=0,125;    Точка D.

x=-1, y=(½)^-1=2¹=2;          Точка K.

x=-2, y=(½)^-2=2²=4;          Точка M.

x=-3, y=(½)^-3=2³=8;          Точка N.

 Большему значению аргумента х соответствует меньшее значение функции y. Функция y=(¹/₂)^x убывает на всей своей области определения: D (y)=R, так как основание функции  0<(¹/₂)<1.