
- •Билет 2. Метод Крамера.
- •Билет 3. Решение слау 3-его порядка методом Крамера,
- •Условие
- •Решение системы линейных алгебраических уравнений методом Крамера
- •Билет 6. Функция
- •Способы задания функции
- •Понятие обратной функции
- •Основные элементарные функции
- •3) В одной координатной плоскости построить графики функций:
- •4) В одной координатной плоскости построить графики функций:
- •Логарифмические уравнения
- •I. Использование определения логарифма
- •II. Использование свойств логарифма
- •III. Метод подстановки
- •IV. Уравнения, содержащие выражения вида
- •V. Некоторые специальные методы
- •Показательные и логарифмические неравенства
- •Радианная и градусная мера угла Переход от радианной меры к градусной
- •Границы координатных четвертей
- •Нестандартные углы и периодичность
- •Основное тригонометрическое тождество. Тригонометрический круг
- •Значения тригонометрических функций 30, 45 и 60 градусов
- •Формулы сложения
- •Формулы сложения тригонометрических функций
Формулы сложения
Тригонометрические функции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости сторон этих треугольников от острых углов при гипотенузе (или, что эквивалентно, зависимость хорд и высот от центрального угла в круге). Эти функции нашли широчайшее применение в самых разных областях науки. Впоследствии определение тригонометрических функций было расширено, их аргументом теперь может быть произвольное вещественное или даже комплексное число. Наука, изучающая свойства тригонометрических функций, называетсятригонометрией. К тригонометрическим функциям относятся, во-первых, прямые тригонометрические функции: синус (sin x), косинус (cos x); во-вторых, противоположные им тригонометрические функции: секанс (sec x) косеканс (cosec x); и, в-третьих, производные тригонометрические функции: тангенс (tg x), котангенс (ctg x).
Формулы сложения тригонометрических функций
sin (α + β) = sin α · cos β + sin β · cos α
sin (α - β) = sin α · cos β - sin β · cos α
cos (α + β) = cos α · cos β - sin α · sin β
cos (α - β) = cos α · cos β + sin α · sin β
tg (α + β) = (tg α + tg β) ÷ (1 - tg α · tg β)
tg (α - β) = (tg α - tg β) ÷ (1 + tg α · tg β)
ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β - ctg α)
ctg (α - β) = (ctg α · ctg β - 1) ÷ (ctg β + ctg α)
Билет 24. Формулы приведения.
Теорема. Для любого угла φ sin (90° — φ) = cosφ. (1) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Доказательство. Если угол φ оканчивается в 1-й четверти, то угол 90° + φ должен оканчиваться во 2-й четверти. Используя единичный круг, получаем: sin (90° + φ) = BD, cos φ = ОС. Но треугольники ОАС и BOD равны; поэтому BD = ОС. Отсюда и вытекает равенство (1). |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если угол φ оканчивается во 2-й четверти, то угол 90° +φ должен оканчиваться в 3-й четверти. Используя единичный круг, получаем: sin (90°+φ) = — BD, cos φ = —ОС. Треугольники ОАС и BOD равны; поэтому BD = ОС. Следовательно, —BD = —ОС, или sin (90° +φ) = cos φ. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Аналогично можно рассмотреть случаи, когда угол φ оканчивается в 3-й или в 4-й четверти. Тождество (1) легко проверить и в случае, когда конечная сторона углаφ лежит на какой-нибудь оси координат. Предлагаем учащимся самостоятельно убедиться в этом. Из доказанного тождества (1) вытекает ряд других важных тождеств. Заменив в (1) φ на — φ, получаем: sin (90° — φ) = cos (—φ) = cos φ. (2) Чтобы получить аналогичную формулу для cos (90° — φ), заменим в (2) φ на 90° — φ. В результате получаем: или sin [90° — (90° — φ)] = cos (90° — φ), Итак, sin φ = cos (90° — φ). cos (90° — φ) = sin φ. (3) Из (2) и (3) вытекает:
tg (90° — φ) = ctg φ. . (4) Аналогично,
Формулы sin (90° — φ) = cos φ, tg (90° — φ) == ctg φ, cos (90° — φ) = sin φ, ctg (90° — φ) = tg φ. иногда называют формулами дополнительного угла. Это связано с тем, что углы 90° —φ и φ дополняют друг друга до прямого угла. Эти формулы очень просто запомнить: одна функция заменяется на другую, сходную с ней (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс). Например, sin 40° = cos 50°; tg 70° = ctg 20° и т. д. Теперь получим формулы для угла 90° + φ. Одну из таких формул мы уже доказали выше: sin (90° + φ) = cos φ. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Остальные формулы легко получаются из формул дополнительного угла и свойства четности (нечетности) тригонометрических функций. Имеем: cos (90° + φ) = cos [90° — (— φ)] = sin (— φ) = —sin φ; tg (90° + φ) = tg [90°— (— φ)] = ctg(— φ) = —ctg φ; ctg (90° + φ) = ctg [90° — (— φ)] = tg (— φ) = — tg φ. Исходя из этих формул, можно получить формулы для углов 180° ± φ. Например, sin (180° + φ) = sin [90° + (90°+ φ)] = cos (90° + φ) = —sin φ; sin (180° — φ) = sin [90° + (90° — φ)] = cos (90° — φ) = sin φ. Аналогично доказываются формулы cos (180° + φ) = — cos φ; cos (180° — φ) = — cos φ. Чтобы получить соответствующие формулы для тангенса и котангенса, можно воспользоваться выведенными соотношениями для синуса и косинуса, учитывая, что tg φ = sin φ/cos φ, ctg φ = cos φ/sin φ. Однако в данном случае лучше всего исходить из того, что угол 180° является периодом функций tg φ и ctg φ. Отсюда сразу же получаем: tg (180° + φ) = tg φ, tg (180° — φ) == tg (—φ) = — tg φ, ctg (180° + φ) = ctg φ, ctg (180° — φ) = ctg (— φ) = — ctg φ. Из формул для углов 180° ± φ можно получить аналогичные формулы для углов 270° ±φ. Формулы для углов 360° ± φ легко получаются, если учесть, что угол 360° является общим периодом тригонометрических функций. Подробно останавливаться на этом мы не будем. В таблице приведены нужные нам формулы. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Заучивать эти формулы нет нужды. Достаточно помнить следующее: 1) если в формуле содержатся углы 180° и 360° (π и 2π), то наименование функции не изменяется; если же в формуле содержатся углы 90° и 270° (π/2 и 3π/2), то наименование функции меняется на сходное (синус на косинус, тангенс на котангенс и т. д.); 2) чтобы определить знак в правой части формулы (+ или—), достаточно, считая угол φ острым, определить знак выражения, стоящего в левой части формулы. Пусть, например, нужно определить tg (90° + φ). Прежде всего мы замечаем, что в формуле содержится угол 90°. Поэтому в правой части искомой формулы должен стоять ctg φ. Чтобы определить знак перед ctg φ, предположим, что угол φ острый. Тогда угол 90° +φ должен оканчиваться во 2-й четверти. Но тангенс угла, оканчивающегося во 2-й четверти, отрицателен. Поэтому перед ctg φ нужно взять знак —. Итак, tg (90° + φ) = — ctg φ. Аналогично устанавливается формула cos (180° — φ) = — cos φ. Поскольку в формуле содержится угол в 180°, наименование функции не изменяется. Если угол φ острый, то угол 180°—φ должен оканчиваться во 2-й четверти. Но косинус угла, оканчивающегося во 2-й четверти, отрицателен. Поэтому в правой части формулы должен стоять знак —. Полученные выше формулы носят название формул приведения. Причины такого названия будут выяснены далее. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Билет 25. Тригонометрические функции двойного аргумента.
Тригонометрические функции двойного и тройного аргумента
![]()
![]()
![]()
![]()
![]()
Билет 26. Тригонометрические функции половинного аргумента.
Тригонометрические функции половинного аргумента
(выбор
знака зависит от того, в какой четверти
находится угол ![]() )
)
![]()
![]()
Выражение тригонометрической функции через тангенс половинного аргумента
![]()
![]()
![]()
![]()
Билет 27. Преобразование суммы и разности тригонометрических функций в произведение.



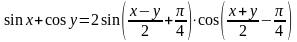


Билет 28. Преобразование произведения тригонометрических функций в сумму.







