Значения тригонометрических функций 30, 45 и 60 градусов
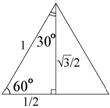Рассмотрим
равносторонний треугольник со стороной,
равной 1. Высота этого треугольника
равна 
и делит сторону пополам.
Из
левого прямоугольного треугольника
найдём:
.
Т.к. 
,
а 
,
то
.
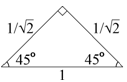
Из
прямоугольного равнобедренного
треугольника с гипотенузой, равной 1 и
острыми углами по 450 найдём:
.
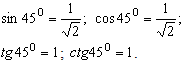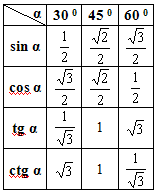
Сведём
все полученные результаты в
таблицу:
Билет 20. Четность и нечетность тригонометрических функций.
Функция y = f(x) называется четной, если для любого x из области определения функции выполняется равенство f(-x) = f(x).
четные функции: y = /x/, y = x2, y = cos x
График четной функции симметричен относительно оси OY.
Функция y = f(x) называется нечетной, если для любого x из области определения функции выполняется равенство f(-x) = - f(x).
нечетные функции: y = 1/x, y = x3, y = sin x, y = tg x, y = ctg x, y = arcsin x, y = arctg x
График нечетной функции симметричен относительно начала координат O.
Из определения четной и нечетной функции следует, что область определения X как четной, так и нечетной функции должна обладать следующим свойством: если x принадлежит X, то и -x принадлежит X, т.е. X - симметричное относительно начала координат O множество.
Функция F(x) называется ни четной, ни нечетной во всех остальных случаях. sin α, tg &alpha, ctg &alpha и cosec &alpha - функции нечетные. sin(- α) = - sin α tg(- α) = - tg α; ctg(- α) = - ctg α; cosec(- α) = - cosec α. cos α и sec α - функции четные. cos(- α) = cos α; sec(- α) = sec α.
Билет 21. Периодичность тригонометрических функций.
Периодичность функций sin φ и cos φ
|
|
Предположим, что вектор ОА = (х, у) единичной длины образует с осью абсцисс угол φ. Если сделать полный оборот вектора ОА вокруг точки О против часовой стрелки, то получится уголφ + 360°. Но вектор ОА при этом займет первоначальное положение, а потому координаты его х и у не изменятся. |
|
Следовательно, у = sin φ = sin(φ + 360°), x = cos φ = cos (φ+ 360°). Эти соотношения показывают, что значения функций sin φ и cos φ не изменяются, если их аргумент, увеличить на 360°. Пусть f(х) есть некоторое выражение, зависящее от переменной величины х. (Например, f(х) = x2, f(х) = sin x и т. д.) Тогда равенство y = f(х) Определяет у как функцию аргумента х. |
|
Если при любых допустимых значениях аргумента х f(x+T) = f (х), где Т — некоторое отличное от нуля число, то функция f (x) называется периодической, а число Т — ее периодом. Согласно этому определению функции sin x и cos х являются периодическими с периодом Т = 360°. При n полных оборотах вектора ОА против часовой стрелки образуется угол φ + 360°n, а по часовой стрелке — угол φ — 360°n. В каждом из этих случаев координаты х и у вектора не изменяются, а потому не изменяются sin φ и cos φ. Таким образом, cos φ = cos (φ + 360°n), sin φ = sin (φ + 360°n), (1) где n — любое целое число (положительное, отрицательное или нуль). Формулы (1) показывают, что каждый из углов 360°; 720°; 1080°; ... (n = 1, 2, 3, . . .), — 360°; —720°; —1080°; ... (n = — 1, —2, —3, . . .) является периодом функции sin φ и cos φ. Таким образом, эти периодические функции имеют бесконечное множество периодов. Можно доказать, что любая периодическая функция (а не только sin φ и cos φ) имеет бесконечное множество периодов. Говоря о периоде функции, удобно из бесконечного множества всех ее периодов иметь в виду какой-нибудь один вполне определенный период. Обычно выделяют наименьший положительный период функции. Из всех рассмотренных выше периодов функции sin φ наименьшим положительным периодом является угол в 360°. Но, может быть, существует еще меньший угол, который мы просто упустили из виду, но который, Также является периодом функции sin φ? Чтобы решить этот вопрос, предположим, что наименьший положительный период функции sin φ равен Т. Тогда при любом φ sin (φ + Т) = sin φ. В частности, при φ = 0 получаем: sinТ = sin 0° = 0. Но нулю равны синусы лишь тех положительных углов, которые кратны углу в 180° , то есть углов в 180°, 360°, 540° и т. д. Поэтому единственным «конкурентом» для угла » 360° является угол в 180°. Составляет ли он период функции sin φ? Если бы это было так, то равенство sin (φ + 180°) = sin φ должно было бы выполняться при всех значениях φ. В частности, при φ = 90° мы получили бы sin 270° = sin 90°. Ho sin 270° = —1, a sin 90° = 1 . Поэтому угол в 180° не является периодом функции sin φ. Остается признать, что периодом (то есть наименьшим положительным периодом) функции sin φ является угол в 360°. Аналогично можно доказать, что периодом функции cos φ также является угол в 360° |
|
Билет 23. Формулы сложения