
- •Билет 2. Метод Крамера.
- •Билет 3. Решение слау 3-его порядка методом Крамера,
- •Условие
- •Решение системы линейных алгебраических уравнений методом Крамера
- •Билет 6. Функция
- •Способы задания функции
- •Понятие обратной функции
- •Основные элементарные функции
- •3) В одной координатной плоскости построить графики функций:
- •4) В одной координатной плоскости построить графики функций:
- •Логарифмические уравнения
- •I. Использование определения логарифма
- •II. Использование свойств логарифма
- •III. Метод подстановки
- •IV. Уравнения, содержащие выражения вида
- •V. Некоторые специальные методы
- •Показательные и логарифмические неравенства
- •Радианная и градусная мера угла Переход от радианной меры к градусной
- •Границы координатных четвертей
- •Нестандартные углы и периодичность
- •Основное тригонометрическое тождество. Тригонометрический круг
- •Значения тригонометрических функций 30, 45 и 60 градусов
- •Формулы сложения
- •Формулы сложения тригонометрических функций
Билет 1. Линейные дифференциальные уравнения второго порядка |
|||||||||||||||||||||||||
Дифференциальное
уравнение второго порядка имеет вид Определение. Общим
решением уравнения второго порядка
называется такая функция Определение. Линейным
однородным уравнением второго порядка
называется уравнение Уравнение Определение. Уравнение Известно,
что квадратное уравнение
имеет
решение, зависящее от дискриминанта Пример
4. Решить
уравнение Решение. Дискриминант
этого квадратного уравнения Покажем, как по виду корней характеристического уравнения найти общее решение однородного линейного уравнения второго порядка. Если Если
корни характеристического уравнения
одинаковы, т.е. Если
же характеристическое уравнение имеет
комплексные корни
,
то Пример
5. Найти
общее решение уравнения Решение. Составим
характеристическое уравнение для
данного дифференциального уравнения: Пример
6. Решить
уравнение Решение. Характеристическое
уравнение Пример
7. Решить
уравнение Решение. Характеристическое
уравнение
данного
однородного линейного уравнения мы
уже решили выше в примере 4. Корни этого
уравнения Общее
решение линейного неоднородного
уравнения второго порядка с постоянными
коэффициентами, т.е. уравнения вида
,
записывается в виде Укажем способ, позволяющий найти частное решение неоднородного уравнения по виду правой части. Заметим, что это возможно лишь в случаях, когда правая часть уравнения является функцией определенного вида. 1. Пусть
2.
Если
при
при
,
частное
решение
ищут
в виде
при
находим
по
формуле 2. Пусть
теперь Таким образом, имеем:
если
,
,
то
если
если
,
то
Пример
8. Решить
уравнение
Решение. Составим
характеристическое уравнение
соответствующего данному уравнению
однородного уравнения Складывая
общее решение однородного уравнения
и найденное частное решение неоднородного
уравнения, получим
:
Пример
9. Решить
уравнение Решение. Составим
характеристическое уравнение
соответствующего однородного
уравнения Его
корни
Правая
часть уравнения Найдем
неизвестный коэффициент
,
подставляя
в
уравнение. Для этого найдем
и
Пример
10. Решить
уравнение
Решение. Характеристическое
уравнение Правая
часть неоднородного уравнения
представляет собой произведение
многочлена первой степени
Подставим
далее
,
и
в
неоднородное уравнение. Имеем
Сократим
обе части уравнения на
Преобразуем
левую часть полученного тождества:
В заключение приведем таблицу, облегчающую решение линейных уравнений с правой частью .
Таблица
Окончание табл.
|
Билет 2. Метод Крамера.
Метод
Крамера применяется для решения систем
линейных алгебраических уравнений
(СЛАУ), в которых число неизвестных
переменных равно числу уравнений и
определитель основной матрицы отличен
от нуля. В этой статье мы разберем как
по методу Крамера находятся неизвестные
переменные и получим формулы. После
этого перейдем к примерам и подробно
опишем решение систем линейных
алгебраических уравнений методом
Крамера.
Пусть нам требуется
решить систему линейных уравнений
вида
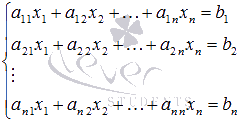 где x1,
x2,
…, xn –
неизвестные переменные, ai
j , i
= 1, 2, …, n, j = 1, 2, …, n –
числовые коэффициенты, b1,
b2,
…, bn -
свободные члены. Решением СЛАУ называется
такой набор значений x1,
x2,
…, xn при
которых все уравнения системы обращаются
в тождества.
В матричном виде эта
система может быть записана как A
⋅
X = B,
где
где x1,
x2,
…, xn –
неизвестные переменные, ai
j , i
= 1, 2, …, n, j = 1, 2, …, n –
числовые коэффициенты, b1,
b2,
…, bn -
свободные члены. Решением СЛАУ называется
такой набор значений x1,
x2,
…, xn при
которых все уравнения системы обращаются
в тождества.
В матричном виде эта
система может быть записана как A
⋅
X = B,
где 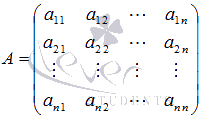 -
основная матрица системы, ее элементами
являются коэффициенты при неизвестных
переменных,
-
основная матрица системы, ее элементами
являются коэффициенты при неизвестных
переменных, ![]() -
матрица – столбец свободных членов,
а
-
матрица – столбец свободных членов,
а ![]() -
матрица – столбец неизвестных переменных.
После нахождения неизвестных переменных x1,
x2,
…, xn,
матрица
становится
решением системы уравнений и равенство A
⋅
X = B обращается
в тождество
-
матрица – столбец неизвестных переменных.
После нахождения неизвестных переменных x1,
x2,
…, xn,
матрица
становится
решением системы уравнений и равенство A
⋅
X = B обращается
в тождество ![]() .
Будем
считать, что матрица А –
невырожденная, то есть, ее определитель
отличен от нуля. В этом случае система
линейных алгебраических уравнений
имеет единственное решение, которое
может быть найдено методом Крамера.
(Методы решения систем при
.
Будем
считать, что матрица А –
невырожденная, то есть, ее определитель
отличен от нуля. В этом случае система
линейных алгебраических уравнений
имеет единственное решение, которое
может быть найдено методом Крамера.
(Методы решения систем при ![]() разобраны
в разделе решение
систем линейных алгебраических
уравнений).
Метод
Крамера основывается на двух свойствах
определителя матрицы:
разобраны
в разделе решение
систем линейных алгебраических
уравнений).
Метод
Крамера основывается на двух свойствах
определителя матрицы:
Определитель квадратной матрицы
 равен
сумме произведений элементов какой-либо
строки (столбца) на их алгебраические
дополнения:
равен
сумме произведений элементов какой-либо
строки (столбца) на их алгебраические
дополнения:

Сумма произведений элементов какой-либо строки (столбца) квадратной матрицы на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю:

Итак,
приступим к нахождению неизвестной
переменной x1.
Для этого умножим обе части первого
уравнения системы на А1
1 ,
обе части второго уравнения – на А2
1 ,
и так далее, обе части n-ого уравнения
– на Аn
1 (то
есть, уравнения системы умножаем на
соответствующие алгебраические
дополнения первого столбца
матрицы А):
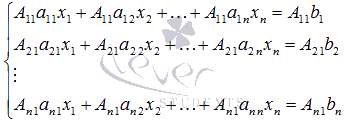 Сложим
все левые части уравнения системы,
сгруппировав слагаемые при неизвестных
переменных x1,
x2,
…, xn,
и приравняем эту сумму к сумме всех
правых частей уравнений:
Сложим
все левые части уравнения системы,
сгруппировав слагаемые при неизвестных
переменных x1,
x2,
…, xn,
и приравняем эту сумму к сумме всех
правых частей уравнений:
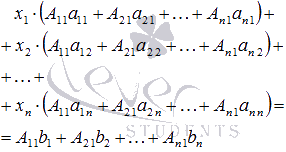 Если
обратиться к озвученным ранее свойствам
определителя, то имеем
Если
обратиться к озвученным ранее свойствам
определителя, то имеем
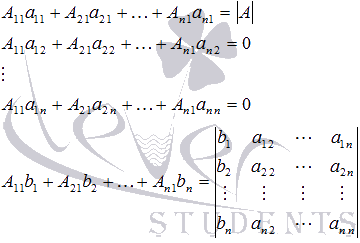 и
предыдущее равенство примет
вид
и
предыдущее равенство примет
вид
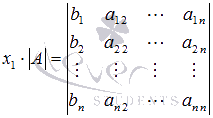 откуда
откуда
 Аналогично
находим x2.
Для этого умножаем обе части уравнений
системы на алгебраические дополнения
второго столбца матрицы А:
Аналогично
находим x2.
Для этого умножаем обе части уравнений
системы на алгебраические дополнения
второго столбца матрицы А:
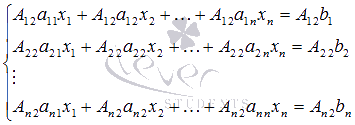 Складываем
все уравнения системы, группируем
слагаемые при неизвестных переменных x1,
x2,
…, xn и
применяем свойства
определителя:
Складываем
все уравнения системы, группируем
слагаемые при неизвестных переменных x1,
x2,
…, xn и
применяем свойства
определителя:
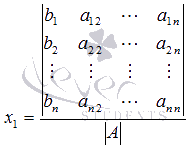
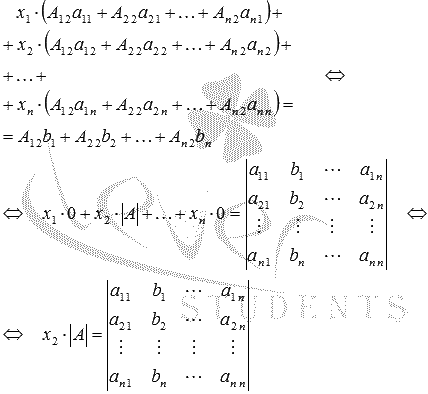 Откуда
Откуда
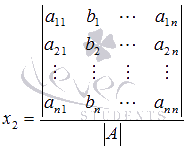 .
Аналогично
находятся оставшиеся неизвестные
переменные.
Если обозначить
.
Аналогично
находятся оставшиеся неизвестные
переменные.
Если обозначить
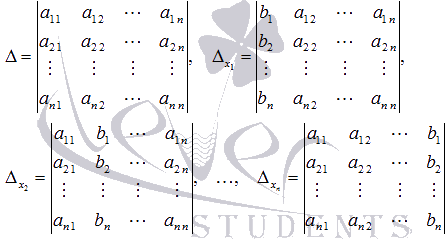 то
получаем формулы
для нахождения неизвестных переменных
по методу Крамера
то
получаем формулы
для нахождения неизвестных переменных
по методу Крамера ![]() .
Замечание.
Если
система линейных алгебраических
уравнений однородная, то есть
.
Замечание.
Если
система линейных алгебраических
уравнений однородная, то есть ![]() ,
то она имеет лишь тривиальное
решение
,
то она имеет лишь тривиальное
решение ![]() (при
(при ![]() ).
Действительно, при нулевых свободных
членах все определители
).
Действительно, при нулевых свободных
членах все определители ![]() будут
равны нулю, так как будут содержать
столбец нулевых элементов. Следовательно,
формулы
дадут
.
Запишем алгоритм
решения систем линейных алгебраических
уравнений методом Крамера.
будут
равны нулю, так как будут содержать
столбец нулевых элементов. Следовательно,
формулы
дадут
.
Запишем алгоритм
решения систем линейных алгебраических
уравнений методом Крамера.
Вычисляем определитель основной матрицы системы
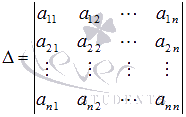 и
убеждаемся, что он отличен от нуля.
и
убеждаемся, что он отличен от нуля.
Находим определители
 которые
являются определителями матриц,
полученных из матрицы А заменой k-ого столбца
(k
= 1, 2, …, n)
на столбец свободных членов.
которые
являются определителями матриц,
полученных из матрицы А заменой k-ого столбца
(k
= 1, 2, …, n)
на столбец свободных членов.
Вычисляем искомые неизвестные переменные x1, x2, …, xn по формулам .
Выполняем проверку результатов, подставляя x1, x2, …, xn в исходную СЛАУ. Все уравнения системы должны обратиться в тождества. Можно также вычислить произведение матриц A ⋅ X, если в результате получилась матрица, равная B, то решение системы найдено верно. В противном случае в ходе решения была допущена ошибка.
Разберем
решения нескольких примеров.
Пример.
Найдите
решение неоднородной системы линейных
алгебраических уравнений методом
Крамера  .
Решение.
Основная
матрица системы имеет вид
.
Решение.
Основная
матрица системы имеет вид ![]() .
Вычислим ее определитель по
формуле
.
Вычислим ее определитель по
формуле ![]() :
:
![]() Так
как определитель основной матрицы
системы отличен от нуля, то СЛАУ имеет
единственное решение, и оно может быть
найдено методом Крамера. Запишем
определители
Так
как определитель основной матрицы
системы отличен от нуля, то СЛАУ имеет
единственное решение, и оно может быть
найдено методом Крамера. Запишем
определители ![]() и
и ![]() .
Заменяем первый столбец основной матрицы
системы на столбец свободных членов, и
получаем определитель
.
Заменяем первый столбец основной матрицы
системы на столбец свободных членов, и
получаем определитель 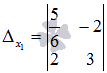 .
Аналогично заменяем второй столбец
основной матрицы на столбец свободных
членов, и получаем
.
Аналогично заменяем второй столбец
основной матрицы на столбец свободных
членов, и получаем 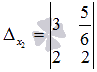 .
Вычисляем
эти определители:
.
Вычисляем
эти определители:
 Находим
неизвестные переменные x1 и x2 по
формулам
Находим
неизвестные переменные x1 и x2 по
формулам ![]() :
:
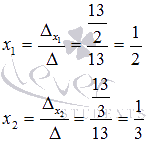 Выполним
проверку. Подставим полученные
значения x1 и x2 в
исходную систему уравнений:
Выполним
проверку. Подставим полученные
значения x1 и x2 в
исходную систему уравнений:
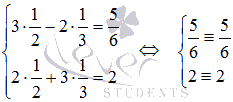 Оба
уравнения системы обращаются в тождества,
следовательно, решение найдено
верно.
Ответ:
Оба
уравнения системы обращаются в тождества,
следовательно, решение найдено
верно.
Ответ: ![]() .
Некоторые
элементы основной матрицы СЛАУ могут
быть равны нулю. В этом случае в уравнениях
системы будут отсутствовать соответствующие
неизвестные переменные. Разберем
пример.
Пример.
Найдите
решение системы линейных уравнений
методом Крамера
.
Некоторые
элементы основной матрицы СЛАУ могут
быть равны нулю. В этом случае в уравнениях
системы будут отсутствовать соответствующие
неизвестные переменные. Разберем
пример.
Пример.
Найдите
решение системы линейных уравнений
методом Крамера 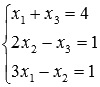 .
Решение.
Перепишем
систему в виде
.
Решение.
Перепишем
систему в виде 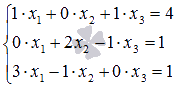 ,
чтобы стало видно основную матрицу
системы
,
чтобы стало видно основную матрицу
системы 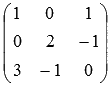 .
Найдем ее определитель по
формуле
.
Найдем ее определитель по
формуле
 Имеем
Имеем
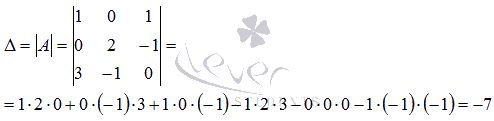 Определитель
основной матрицы отличен от нуля,
следовательно, система линейных уравнений
имеет единственное решение. Найдем его
методом Крамера. Вычислим
определители
Определитель
основной матрицы отличен от нуля,
следовательно, система линейных уравнений
имеет единственное решение. Найдем его
методом Крамера. Вычислим
определители ![]() :
:
 Таким
образом,
Таким
образом,
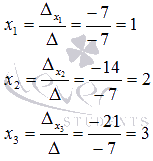 Ответ:
Ответ: ![]() .
Обозначения
неизвестных переменных в уравнениях
системы могут отличаться от x1,
x2,
…, xn.
Это не влияет на процесс решения. А вот
порядок следования неизвестных переменных
в уравнениях системы очень важен при
составлении основной матрицы и необходимых
определителей метода Крамера. Поясним
этот момент на примере.
Пример.
Используя
метод Крамера, найдите решение системы
трех линейных алгебраических уравнений
с тремя неизвестными
.
Обозначения
неизвестных переменных в уравнениях
системы могут отличаться от x1,
x2,
…, xn.
Это не влияет на процесс решения. А вот
порядок следования неизвестных переменных
в уравнениях системы очень важен при
составлении основной матрицы и необходимых
определителей метода Крамера. Поясним
этот момент на примере.
Пример.
Используя
метод Крамера, найдите решение системы
трех линейных алгебраических уравнений
с тремя неизвестными 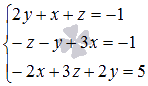 .
Решение.
В
данном примере неизвестные переменные
имеют другое обозначение
(x, y и z вместо x1, x2 и x3).
Это не влияет на ход решения, но будьте
внимательны с обозначениями переменных.
В качестве основной матрицы системы
НЕЛЬЗЯ брать
.
Решение.
В
данном примере неизвестные переменные
имеют другое обозначение
(x, y и z вместо x1, x2 и x3).
Это не влияет на ход решения, но будьте
внимательны с обозначениями переменных.
В качестве основной матрицы системы
НЕЛЬЗЯ брать 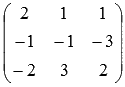 .
Необходимо сначала упорядочить
неизвестные переменные во всех уравнениях
системы. Для этого перепишем систему
уравнений как
.
Необходимо сначала упорядочить
неизвестные переменные во всех уравнениях
системы. Для этого перепишем систему
уравнений как 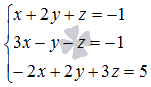 .
Теперь основную матрицу системы хорошо
видно
.
Теперь основную матрицу системы хорошо
видно ![]() .
Вычислим ее определитель:
.
Вычислим ее определитель:
 Определитель
основной матрицы отличен от нуля,
следовательно, система уравнений имеет
единственное решение. Найдем его методом
Крамера. Запишем определители
Определитель
основной матрицы отличен от нуля,
следовательно, система уравнений имеет
единственное решение. Найдем его методом
Крамера. Запишем определители ![]() (обратите
внимание на обозначения) и вычислим
их:
(обратите
внимание на обозначения) и вычислим
их:
 Осталось
найти неизвестные переменные по
формулам
Осталось
найти неизвестные переменные по
формулам ![]() :
:
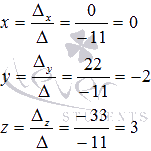 Выполним
проверку. Для этого умножим основную
матрицу на полученное решение
Выполним
проверку. Для этого умножим основную
матрицу на полученное решение ![]() (при
необходимости смотрите раздел операции
над матрицами):
(при
необходимости смотрите раздел операции
над матрицами):
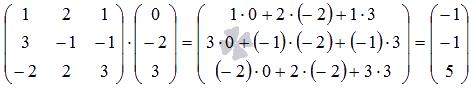 В
результате получили столбец свободных
членов исходной системы уравнений,
поэтому решение найдено верно.
Ответ: x
= 0, y = -2, z = 3.
Пример.
Решите
методом Крамера систему линейных
уравнений
В
результате получили столбец свободных
членов исходной системы уравнений,
поэтому решение найдено верно.
Ответ: x
= 0, y = -2, z = 3.
Пример.
Решите
методом Крамера систему линейных
уравнений 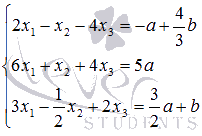 ,
где a и b –
некоторые действительные
числа.
Решение.
Вычислим
определитель основной матрицы
системы:
,
где a и b –
некоторые действительные
числа.
Решение.
Вычислим
определитель основной матрицы
системы:
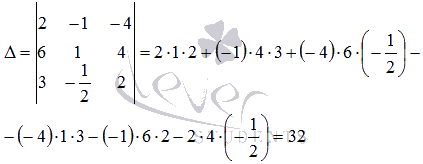 Определитель
отличен от нуля, следовательно, можно
применить метод Крамера.
Определитель
отличен от нуля, следовательно, можно
применить метод Крамера.
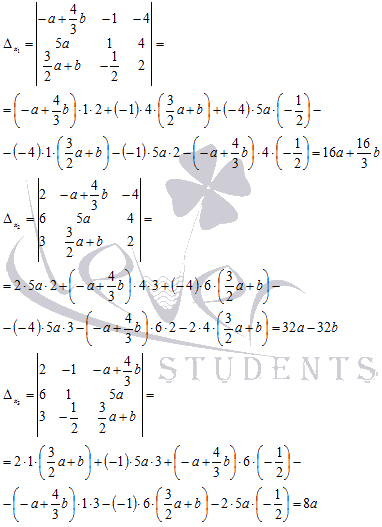 Находим
неизвестные переменные
Находим
неизвестные переменные
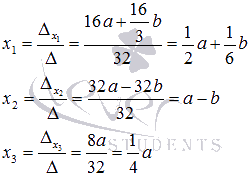 Рекомендуем
проверить полученные
результаты.
Ответ:
Рекомендуем
проверить полученные
результаты.
Ответ: ![]() .
Пример.
Найдите
решение системы уравнений
.
Пример.
Найдите
решение системы уравнений ![]() методом
Крамера,
методом
Крамера, ![]() -
некоторое действительное
число.
Решение.
Вычислим
определитель основной матрицы
системы:
-
некоторое действительное
число.
Решение.
Вычислим
определитель основной матрицы
системы: ![]() .Область
значений выражения
.Область
значений выражения ![]() есть
интервал
есть
интервал ![]() ,
поэтому
,
поэтому ![]() при
любых действительных значениях
.
Следовательно, система уравнений имеет
единственное решение, которое может
быть найдено методом Крамера.
Вычисляем
и
:
при
любых действительных значениях
.
Следовательно, система уравнений имеет
единственное решение, которое может
быть найдено методом Крамера.
Вычисляем
и
:
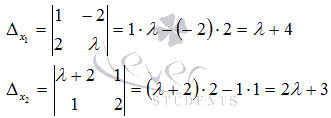 Таким
образом,
Таким
образом, ![]() .
Выполним
проверку:
.
Выполним
проверку:
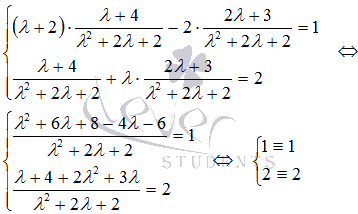 Уравнения
системы обращаются в тождества,
следовательно, решение найдено
верно.
Ответ:
Уравнения
системы обращаются в тождества,
следовательно, решение найдено
верно.
Ответ: ![]() .
Пример.
Решите
систему линейных алгебраических
уравнений методом Крамера
.
Пример.
Решите
систему линейных алгебраических
уравнений методом Крамера 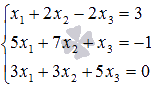 .
Решение.
Вычислим
определитель основной матрицы системы
уравнений:
.
Решение.
Вычислим
определитель основной матрицы системы
уравнений:
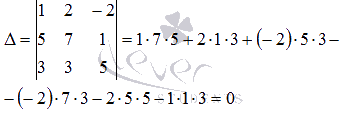 Определитель
основной матрицы равен нулю, следовательно,
метод Крамера не подходит для решения
такой системы уравнений.
Пример.
Методом
Крамера найдите решение СЛАУ
Определитель
основной матрицы равен нулю, следовательно,
метод Крамера не подходит для решения
такой системы уравнений.
Пример.
Методом
Крамера найдите решение СЛАУ ![]() .
Решение.
Эта
система однородная, так как все свободные
члены равны нулю. Определитель основной
матрицы отличен от нуля
.
Решение.
Эта
система однородная, так как все свободные
члены равны нулю. Определитель основной
матрицы отличен от нуля ![]() ,
поэтому ее единственным решением
является x1 =
0, x2 =
0.
О таких СЛАУ мы уже упоминали выше в
замечании.
Ответ: x1 =
0, x2 =
0.
Пример.
Найдите
решение системы четырех линейных
алгебраических уравнений
,
поэтому ее единственным решением
является x1 =
0, x2 =
0.
О таких СЛАУ мы уже упоминали выше в
замечании.
Ответ: x1 =
0, x2 =
0.
Пример.
Найдите
решение системы четырех линейных
алгебраических уравнений 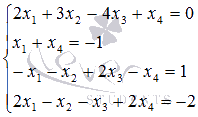 содержащую
четыре неизвестных переменных.
Решение.
Сразу
скажем, что не будем подробно описывать
вычисление определителей матриц, так
как это выходит за рамки данной
статьи.
Вычислим определитель
основной матрицы системы, разложив его
по элементам второй строки:
содержащую
четыре неизвестных переменных.
Решение.
Сразу
скажем, что не будем подробно описывать
вычисление определителей матриц, так
как это выходит за рамки данной
статьи.
Вычислим определитель
основной матрицы системы, разложив его
по элементам второй строки:
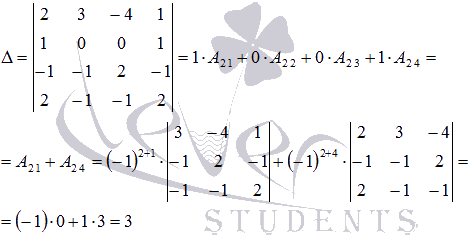 Определитель
основной матрицы системы отличен от
нуля, поэтому можно воспользоваться
методом Крамера для решения
системы.
Найдем
Определитель
основной матрицы системы отличен от
нуля, поэтому можно воспользоваться
методом Крамера для решения
системы.
Найдем ![]() :
:
 аналогично
вычисляются
аналогично
вычисляются
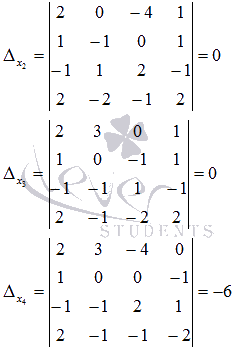 Таким
образом,
Таким
образом,
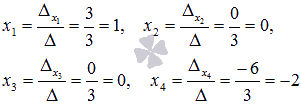 Ответ:
Ответ: ![]() .
Подведем
итог.
Метод
Крамера позволяет находить решение
систем линейных алгебраических уравнений,
если определитель основной матрицы
отличен от нуля. По сути метод сводится
к вычислению определителей матриц
порядка n на
n и
применению соответствующих формул для
нахождения неизвестных переменных.
.
Подведем
итог.
Метод
Крамера позволяет находить решение
систем линейных алгебраических уравнений,
если определитель основной матрицы
отличен от нуля. По сути метод сводится
к вычислению определителей матриц
порядка n на
n и
применению соответствующих формул для
нахождения неизвестных переменных.
