2. Решение задач на полуограниченной прямой методом продолжений.

Решим следующие задачи:

1. Решить уравнение

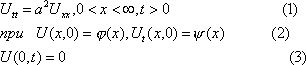
Р ассмотрим функции ( x) и (x), являющиеся нечетным продолжением функций (2):

(4)

Ф ункция

будет являться решением задачи (1) – (3), т.к. U(x, t) у довлетворяет уравнению (1) как суперпозиция прямой и обратных волн и U(0, t)=0 в силу Леммы 1. Кроме того U(x, t) у довлетворяет начальному условию при x>0 и t>0:

Т аким образом, рассматривая U(x, t) т олько для x>=0 и t>0, мы получим функцию, удовлетворяющую всем условиям поставленной задачи. Возвращаясь к прежним функциям, получаем:

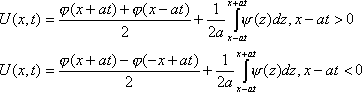(6)

т.е. до момента времени t=x/a в лияние границ не сказывается и решение совпадает с решением для бесконечной прямой.

2. В случае свободного конца задача решается аналогично. Здесь U_x(0, t)=0, поэтому берем четное продолжение (x) и (x) н а отрицательную полуось:

и получаем

- решение задачи.

Возвращаясь к прежним функциям, получаем:

( 7)

Таким образом, получаем следующие правила:

1) Для решения задачи на полуограниченной прямой с граничным условием U(0, t) начальные функции нужно продолжать (на всю прямую) нечетным образом на отрицательную часть прямой.

2) Для решения задачи на полуограниченной прямой с граничным условием U_x(0, t) начальные данные нужно продолжить (на всю прямую) четным образом на отрицательную часть прямой.

Для ограниченной с обеих сторон струны (U(x, 0)=U(x, l)=0 – концы закреплены, U_х(x, 0)=U_х(x, l)=0 – концы свободны); м ожно воспользоваться методом Даламбера, для чего надо продолжить функции (x) и (x) н ечетно или четно на отрезок (-l, 0), а затем периодически на всю ось.

Пример. Концы струны длины l з акреплены на концах x=0, x=l. Начальное отклонение

. Начальные скорости равны нулю. Найти смещение U(x, t).

Математическая постановка задачи:

Решение: Продолжим  (x) и (x) н ечетно на (-l, 0), а затем периодически на всю ось, тогда получим:

.

По формуле Даламбера

#7,8

1. Р ешение задачи Коши для двухмерного волнового уравнения. Формула Пуассона.

Рассмотрим вспомогательную функциюU(r, t) - усреднение искомого решения на S^r_M сфере с центром в точке M и радиусом r. (3)

Если обозначить через  э лемент телесного угла под которым виден из точки M э лемент площади , то  =r² . Поэтому (4)

Из (3) при r –>0, получаемU(0, t)=U(M, t) . (5)

Т.о., для нахождения функции U(M, t) достаточно найти функциюU(r, t).

Лемма. Справедливо соотношениеU = _r(U ) =  (U ) (6)

(ЛапласианU берется по координатам точки M, а _r(U ) - по переменной r; ниже будем опускать значок r у оператора )

П усть D^r_M - обстать, ограниченная сферической поверхностью S^r_M . По формуле Остроградского имеем

. (7)

Применяя к последнему интегралу формулу (4), получаем

. (8)

С другой стороны,

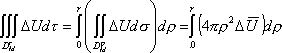. (9)

Из (8) и (9) следует, что

(10)

Продифференцируем (10) по :

. (11)

Что и требовалось доказать. Лемма доказана.

Предположим теперь, что решение задачи (1) – (2)существует. Тогда, применяя операцию усреднения по сфере S^r_M к тождеству a²UU_tt и используя Лемму получаем

или

или (12)

Обозначим rU через V.

Т огда и выражение (12) примет вид

(13)

т.е. функция V(r, t) удовлетворяет одномерному волновому уравнению.

Применяя операцию усреднения к начальным условиям (2), найдем:

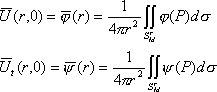(14)

П усть

Т.о., для V(r, t) и меем следующую задачу на полубесконечной прямой: (*)

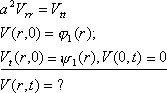Для ее решения начальные функции ₁(r) , ₁(r) н адо продолжить нечетным образом на полупрямую (-, 0) и для продолженных функций  ₂(r) , ₂(r) н аписать формулу Даламбера.

П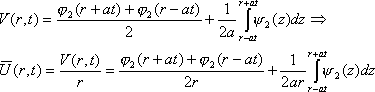 ри этом функции(r) ,(r) будут продолжены четным образом. Для продолженных функций оставим прежние обозначения(r) ,(r). Для функции V(r, t) имеем:

П ри r=0 =>U(0, t) = 0/0. По правилу Лопиталя находим:

( учитывая )

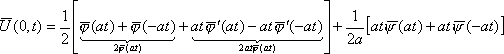. Т.к. (z) и(z) - четные, а’(z) - нечетная, то

. (15)

Теперь можно записать решение задачи, используя (5), (14) при r = at:

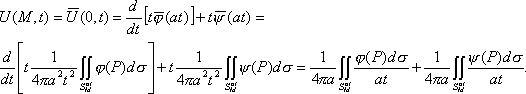( 16)

Продолжение части 1.

Из формулы Кирхгофа можно получить решение задачи Коши для однородного волнового уравнения в двумерном пространстве:

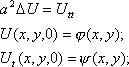( 17)

Если в (16) функции (P) и (P) н е зависят от переменной z, то интегралы по поверхности S^at_M м ожно свести к интегралам по большому кругу этой сферы ^at_M , лежащему в плоскости (x, y).

Интеграл по верхней половине сферы S^at_M р авен

, (18)

где  - угол между нормалями к плоскости (x, y) и к сфере S^at_M в точке P. Имеем

,

г де - координаты точки P₁, x, y - координаты точки наблюдения M. Поэтому (19)

А налогично, (20)

Применяя аналогичное преобразование во втором интеграле формулы Пуассона, получим решение задачи Коши .

3 . Теорема Коши-Ковалевской.

Пусть - целочисленный вектор с неотрицательными компонентами a_j. Через D^af(x) о бозначим производную функции f(x) п орядка |a|=a₁+a₂+...a_n:

, .

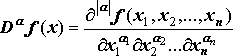. Введём следующие сокращённые обозначения:

О пределение 1. Система N дифференциальных уравнений с N неизвестными функциями

( *)

называется нормальной относительно переменной t, если правые части Ф_i н е содержат производных порядка выше k_i и производных по t порядка выше k_{i -1}, то есть

Например, волновое уравнение, уравнение Лапласа и уравнение теплопроводности нормальны относительно каждой переменной x; волновое уравнение нормально и относительно t.

Определение 2. Функция f(x), x=(x₁,x₂,…,x_n,) называется аналитической в точке х₀, если в некоторой окрестности точки х₀ она представлена в виде равномерно сходящегося степенного ряда:

Д ля нормальной относительно t системы уравнений (*) поставим задачу Коши: найти решение э той системы, удовлетворяющее начальным условиям при t=t₀. (**)

г де _ik(x) - заданные функции в некоторой области G  Rⁿ.

Теорема Ковалевской.

Если все функции _ik(x) аналитичны в некоторой окрестности точки х₀ и все функции Ф_i(x, t,...,U_ja₀a₁...) аналитичны в некоторой окрестности точки (x₀, t₀,...D^a_ij(x₀),...), то задача Коши (*)-(**) имеет аналитическое решение в некоторой окрестности точки (x₀, t₀) и притом единственное в классе аналитических функций.

Д ля доказательства теоремы решение в окрестности точки (x₀, t₀) ищется в виде степенных рядов (***)

И з начальных условий (**) и уравнения (*) последовательно определяются все производные D^a0_t D^a_x U_i в точке (x₀, t₀).

Равномерная сходимость последних рядов в некоторой окрестности точки (x₀, t₀) доказывается методом мажорант. Единственность построенного решения в классе аналитических функций следует из теоремы единственности для аналитических функций.

Заметим, что теорема Ковалевской, несмотря на её общий характер, полностью не решает вопроса о корректности постановки задачи Коши для нормальной системы дифференциальных уравнений.

#9

1 Метод Фурье решения краевых задач гиперболического типа.

Будем искать решение уравнения

( 1) при начальных условиях

( 2) и граничным условиям

, . (3)

Уравнение (1) линейно и однородно, поэтому сумма частных решений также является решением этого уравнения. Суммируя большое число частных решений, можно найти искомое решение.

Представим решение (1) в виде произведения двух функций

( 4)

каждое из которых зависит только от одной переменной.

Дифференцируя дважды уравнение (4), получим из (1):

Или, деля обе части равенства на a²XT, получим:

. (5)

Чтобы функция U(x, t)=X(x)T(t)б ыла решением уравнения (1), равенство (5) должно соблюдаться при всех значениях x и t.

( 6)

Отсюда получаем

Рассмотрим решение уравнения (7).

Из граничных условий находим

Отсюда следует, что функция X(x) д олжна удовлетворять дополнительным условиям

, (9)

т.к. в противном случае T(t)0 и U(x, t)0, в то время как задача состоит в нахождении не тривиального решения.

Таким образом, приходим к следующей задаче, называемой задачей Штурма – Лиувилля:

Н айти те значения параметра , при которых существуют нетривиальные решения задачи (10)

а также найти эти решения. Такие значения параметра  называют собственными значениями, а соответствующие им решения – собственными функциями задачи (10).

П олагая X(x)=e^rx, составим для уравнения (10) характеристическое уравнение

и рассмотрим различные случаи.

1)При >0 задача не имеет не тривиальных решений. Корни характеристического уравнения r =. Общее решение уравнения (10) имеет вид

Г раничные условия дают

О тсюда,

н о

Поэтому .

2)Пусть =0. Тогда оба корня характеристического уравнения равны нулю и

. Из граничных условий X(0)=X(l)=0 находим

. Уравнение (10) не имеет не тривиальных решений.

3)Пусть <0 . Корни характеристического уравнения r=i.

. При x=0, X(0)=C1=0 ;

При x=l, X(l)=C2 sin l=0.

Если X(x)0, то C20 и поэтому

ц елое.

Следовательно, не тривиальные решения возможны только при .

Этим собственным значениям соответствуют собственные функции

.

С истема функций называется ортогональной в интервале [a, b], если интеграл от произведения двух различных функций при nm.

,

т.е. найденные собственные функции ортогональны на интервале [0, l].

Н айдем функцию T(t). Значения удовлетворяют уравнению (8). Его общее решение имеет вид:

, т.к. .

Возвращаясь к задаче (1) – (3), находим

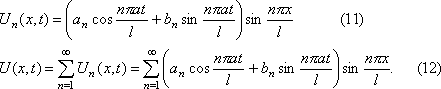
Если ряд (12) расходится или функция, определенная этим рядом не является дифференцируемой, то он не может представлять решение уравнения (1).

Будем подбирать a_n и b_n так, чтобы функция (12) удовлетворяла начальным условиям. Подставляя значение t=0, получим (13)

Продифференцируем ряд (12) по t:

т огда

Ф ункции (13) и (14) показывают, что a_n и nx b_n /l являются коэффициентами разложения функций (x) и (x) в ряд Фурье по синусам в интервале (0,l). Вспоминая формулы для коэффициентов этого разложения, найдем a_n :(15)

. Так как

, то

. (16)

Подставляя выражения для коэффициентов a_n и b_n в ряд (12), мы окончательно найдем решение задачи.

Формула (12) показывает, что в моменты времени t=2l/a, 4l/a,.. струна возвращается в первоначальное состояние, т.е. колебания струны незатухающие, периодические, с периодом T=2l/a.

Решение Фурье тождественно решению методом Даламбера, т.к. применение формулы Даламбера требует, чтобы функции (x) и (x), заданные на (0, l) были продолжены на промежуток (-l, 0) по закону нечетности, а затем с периодом 2l. Но такой способ продолжения равносилен разложению этих функций в ряд Фурье по синусам. (Смирнов, Т.2, стр. 533)

2. Решение неоднородного уравнения колебания струны с неоднородными граничными условиями.

(1)

(2) ( 3)

Ищем решение в виде двух функций

,

где W(x, t) - известная функция, которую подберем так, чтобы для нее выполнялись граничные условия

.

Уравнение (1) запишется в виде

; (4)

Так как W(x, t)- известная функция, то для п олучим такое уравнение

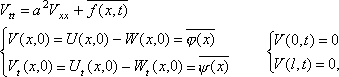
а эту задачу мы решали выше.

3. Решение общей краевой задачи для неоднородного уравнения.

(1) ( 2) (3)

Ищем решение в виде двух функций

, где W(x, t)- известная функция, которую подберем так, чтобы для нее выполнялись граничные условия

. Тогда для V н адо решить уравнение

с начальными и граничными условиями

Эта задача нами уже решена.

Таким образом, если уравнение имеет однородные граничные условия, то его решение ищется в виде суммы двух функций U(x, t) = V(x, t) + W(x, t), где функция W(x, t) п одбирается таким образом, чтобы для нее выполнялись неоднородные граничные условия, а функция V(x, t) б удет решением нового уравнения с однородными граничными условиями.

Подобрать функция для второй краевой задачи (самостоятельно).