1. Полуограниченная прямая. Метод продолжений.

Рассмотрим задачу о распространении волн на полупрямой x>=0. Задача ставится так: найти решение U(x, t)

уравнения U_tt=a²U_xx (1) при начальных условиях U(x, 0)=(x), U_t(x,0)=(x) (2) и граничным условиям U(0,t)=₁(t) [или U_x(0,t)=₂(t)]. (3)

Рассмотрим случай однородного граничного условия.

1) U(0,t)=₁(t) [или U_x(0,t)=₂(t)]

1.Струна с закрепленным концом. 2.Конец струны свободен. (T=0)

Лемма 1. если начальные условия для неограниченной прямой есть нечетные функции относительно точки x=0, т.е. (-x)=-(x) и (-x)=-(x), то соответствующее решение в этой точке равно нулю: U(0,t)=0.

П о формулам Даламбера при x=0 и t>0

так как первое слагаемое равно нулю в силу нечетности (x) , а второе – поскольку интеграл от нечетной функциях в пределах, симметричной относительно начала координат.

Лемма 2. если начальные условия для неограниченной прямой есть четные функции относительно точки x=0, то производная по x соответствующего решения в этой точке равна нулю.

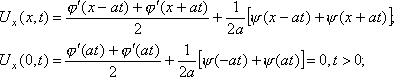
т.к. (-x)=-(x), ’(x)=-’(-x) (производная от функции четной является функцией нечетной).

Опираясь на выше доказанные леммы, решим следующие задачи:

1 . Решить уравнение U_tt=a²U_xx, 0<x<, t>0 (1) при начальных условиях U(x, 0)=(x), U_t(x,0)=(x), (2) U(0,t)=0. (3)

Р ассматриваемые функции (x) и (x), являющиеся нечетным продолжением функции (2): (4)

Функция (5)

б удет решением задачи (1) – (3), так как U(x, t) удовлетворяет уравнению (1) как суперпозиция прямой и обратной волн U(0, t)=0 и в силу Леммы 1. кроме того U(x, t) удовлетворяет начальному условию при x>0 и t>0:

Т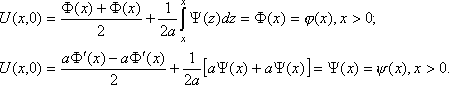 аким образом, рассматривая U(x, t)только для x>=0, t>0, мы получим функцию, удовлетворяющую всем условиям поставленной задачи. Возвращаясь к прежним функциям, получаем:

, если x+at >0,

(6)

, если x+at <0.

Т.е. до момента времени t = x/a влияние границ не сказывается и решение совпадает с решением для бесконечной прямой.

2 .В случае свободного конца задача решается аналогично. Здесь U_x(0,t)=0 , поэтому берем четное продолжение (x) и (x) на отрицательную полуось:

и получаем

- решение задачи. Возвращаясь к прежним функциям, получаем:

, если x-at>0, (7)

Т аким образом, получаем следующие правила:

1) Для решения задачи на полуограниченной прямой с граничным условием U(0,t)=0 начальные функции нужно продолжить (на всю прямую) нечетным образом на отрицательную часть прямой.

2) Для решения задачи на полуограниченной прямой с граничным условием U_x(0,t)=0 начальные данные можно продолжить (на всю прямую) четным образом на отрицательную часть прямой.

Д ля ограниченной с обеих сторон струны (U(x,0)=U(x,l)=0 - концы закреплены; U_x(x,0)=U_x(x,l)=0 - концы свободны) можно воспользоваться методом Даламбера, для чего надо продолжить функции (x) и (x) нечетно или четно на отрезок (-l, 0), а затем периодически на всю ось. Пример. Концы струны длинны l закреплены в точках x=0 и x=l. Начальное отклонение

Начальные скорости равны нулю. Найти смещение U(x, t).

Математическая постановка задачи:

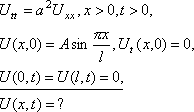
Решение. Продолжением (x) и (x) нечетно на (-l, 0), а затем периодически на всю ось, тогда получим:

П о формуле Даламбера.