3. Рассмотрим систему линейных уравнений

( 9)

Она называется гиперболической, если пара операторов h₁ и h₂ гиперболична, т.е. если ₁  ₂ - действительные.

Система (9) называется эллиптической, если пара операторов h₁ и h₂ - эллиптична. Аналогично определяется параболическая система.

Характеристиками системы (9) называются характеристики пары операторов h₁[U,V] и h₂[U,V].

Систему (9) можно заменить эквивалентной ей системой, называемой характеристической формой системы (9):

( 10)

2. Уравнения характеристик.

Е сли в уравнении второго порядка (11)

п оложить , , то оно сведется к эквивалентной системе (12)

У равнение для нахождения характеристических значений системы (12) имеет вид

или . .

Отсюда следует, что если направление (11) гиперболического (эллиптического, параболического) в некоторой области D, то система (12) будет гиперболической (эллиптической, параболической) в D.

Согласно (12) дифференциальные уравнения характеристик системы (12) имеют вид

и совпадают с уравнениями характеристик, полученных нами ранее.

5. Гиперболические системы с постоянными коэффициентами.

Пусть F₁=F₂=0, а A₁=A₂=B₁=B₂=C₁=C₂=D₁=D₂ - const. Тогда очевидно _1,2 - const. Дифференциальные уравнения характеристик в этом случае имеют вид

, где a₁, a₂ - const.

Следовательно, характеристики есть прямые x – a₁y = d₁; x – a₂y = d₂.

6. Решение задачи Коши для неоднородного волнового уравнения.

Рассмотрим задачу

, (1)

где k, q, p - известные функции точки M.

( 2)

З адачу (1) – (2) разбиваем на две задачи:

1)

2 )

Очевидно, что U = W + V.

Предположим, что мы знаем как решать задачу (3) – (4). Тогда решение задачи Коши (5) – (6) строим следующим образом.

Найдем такую функцию Ф(М, t, ), которая удовлетворяет однородному уравнению (3) для t >  и начальным условиям:

. (7)

по предположению мы умеем решать эту задачу. Тогда искомое решение задачи Коши 2) будет иметь вид

. (8)

В самом деле, по правилу дифференцирования интеграла с переменным верхним пределом по параметру, получаем:

. Используя первое условие из (7), находим

( 9)

Из формул (8), (9) следует, что W(M, t) удовлетворяет начальным условиям (7). Дифференцируя соотношение (9) еще раз по t и используя второе из условий (7), получаем

. Следовательно,

. (10)

Вычислим div(kW) - qW. При этом операцию div(k) можно выполнить под знаком интеграла, тогда

. (11)

Так как функция Ф(М, t, ) является решением уравнения (3), то из формул (10), (11) следует, что функция W(M, t), определяемая формулой (8) является решением уравнения (5), и, следовательно, решением задачи Коши 2).

Замечание. Рассмотренный способ решения задачи (1) – (2) применим и для решения краевой задачи для неоднородного уравнения с однородными условиями. В этом случае вспомогательная функция должна быть решением соответствующей однородной краевой задачи.

Пример. Решить задачу Коши:

.

1 )

2)

Функцию V(x,t) найдем по формуле Даламбера

.

Согласно предыдущему

,

где Ф(x, t, ) - является решением задачи Коши

которое может быть записано по формуле Даламбера в виде

.

П 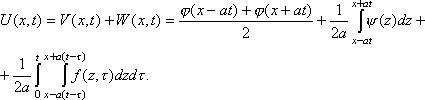оэтому

#6