1. Характеристическое направление и характеристики оператора h[f].

Одним из эффективных методов построения решений и использования свойств решений уравнений в частных производных и систем таких уравнений является метод характеристик.

Как известно, производная функции f(x,y) в фиксированной точке (x,y) по направлению единичного вектора l с компонентами cosa, cosb равна

( 1)

В ыражение , где , можно рассматривать как производную функции f(x,y) в точке (x,y) по направлению единичного вектора с компонентами /

Р ассмотрим оператор , где . Оператор H[f] в любой окрестности точки (x,y) можно рассматривать как производную от f(x,y) по направлению вектора , умноженную на , то есть

Направление называется характеристическим направлением оператора H[f] в фиксированной точке (x,y).

Кривая, в каждой точке которой её касательная имеет характеристическое направление оператора H[f], называется характеристикой оператора H[f].

С огласно определению, в каждой точке характеристики выполняется соотношение: (2)

Оно является дифференциальным уравнением характеристик оператора H и эквивалентно системе(3)

Х арактеристиками уравнения H[f]=0 будем называть характеристики оператора H[f].

Теорема 1. Если функция f(x,y) удовлетворяет уравнению H[f]=0, то есть H[f]º0, то на каждой характеристике оператора H f(x,y)=const.

Вдоль каждой характеристики имеем:

П ринимая во внимание уравнение характеристик (3), получим:

О тсюда и следует, что на каждой характеристике f(x,y)=const.

Ф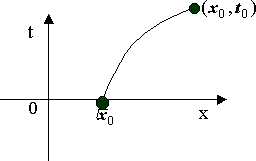 изическая интерпретация. Если y- время (y=t), то теорема 1 означает, что начальное состояние f(x,0) распространяется по характеристикам. Чтобы найти f(x₀,t₀) в произвольной фиксированной точке (x₀,t₀), надо через точку (x₀,t₀) провести характеристику, найти её точку пересечения с осью t=0.

П усть это будет точка . Тогда .

2 . Характеристическая форма оператора.

В ведём понятие характеристик для системы уравнений. Для простоты выкладок ограничимся системой двух уравнений. Для этого рассмотрим сначала оператор над двумя функциями , где , , A, B, C, D- заданные функции от x и у. Операторы над функциями u, v можно рассматривать как умноженные соответственно на - производные по направлениям и , то есть , .Направления дифференцирования и совпадают только в случае, если BC-AD=0, то есть и совпадают только в случае, когда (4)

В этом случае из B/A=D/C следует, что C/A=D/B=k, откуда C=kA, D=kB, k=k(x,y). Следовательно

( 5)

З десь - дифференцирование вдоль кривой , то есть .

Правую часть формулы (5) будем называть характеристической формой оператора .

Х арактеристическая форма пары операторов и .

1) Рассмотрим два оператора

В каждом из этих операторов, согласно предыдущему, дифференцирование производится по двум направлениям. Из операторов h₁ u h₂ можно составить ещё один оператор

, где - некоторая функция.

Р ассмотрим задачу:

Н айти такие значения , чтобы в операторе дифференцирование каждой из функций производилось только в одном направлении.

В операторе дифференцирование функции производится в направлении , а дифференци-рование функции в направлении ,где .

Чтобы эти направления совпадали, необходимо и достаточно, согласно (4), чтобы выполнялось условие (6)

И з (6) находим .

2 ) Для определения  имеем квадратное уравнение. Из него находим два различных значения ₁ и ₂. Эти значения называются характеристическими значениями операторов (h₁, h₂). Каждое из этих значений определяет направление, к дифференцированию вдоль которого сводится оператор . Для каждого из полученных значений  получим свой оператор :

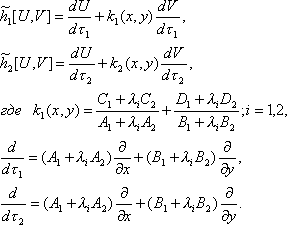( 7)

Т аким образом, для двух исходных операторов h₁ и h₂ м ожно получить два различных оператора и , в каждом из которых дифференцирование функций U и V п роизводится лишь в одном направлении. Эти направления называются характеристическими направлениями пары операндов h₁ и h₂. Будем называть их первым (для ₁) и вторым (для ₂) характеристическими направлениями.

а) если ₁ и ₂ действительны и различны, пара операторов называется гиперболической.

б) если ₁ и ₂ комплексные, пара операторов называется эллиптической.

3) если ₁ = ₂, пара операторов называется параболической.

Кривая, в каждой точке которой ее касательная имеет первое характеристическое направление пары операторов h₁ и h₂, называется характеристикой первого семейства пары операторов h₁ и h₂. Кривая, в каждой точке которой, ее касательная имеет второе характеристическое направление пары операторов h₁ и h₂, называется характеристикой второго семейства пары операторов h₁ и h₂.

В гиперболическом случае имеется два семейства характеристик, дифференциальные уравнения которых имеют вид:

. (8)

В параболическом случае имеется одно семейство характеристик, в эллиптическом – два линейных семейства.

Заметим, что операторы h₁ и h₂ здесь – линейные и их характеристики не зависят от функций U и V.