1. Задача Коши. Метод распространения волн. Формула Даламбера.

Р ассмотрим задачу о колебаниях бесконечной струны (-¥<´<¥), не учитывая влияния отражённых волн.. Рассматривая свободные колебания, мы должны решить однородное уравнение:

(1)при начальных условиях (2)

Н икакие краевые условия на искомую функцию U(x,t) не накладываются. Такая задача называется задачей с начальными условиями или задачей Коши. Метод её решения, который мы сейчас рассмотрим, называется методом Даламбера или методом бегущих волн. Покажем, что общее решение уравнения (1) имеет вид:(3)

где функции f₁ и f₂ предполагаются дважды дифференцируемыми. Последовательно дифференцируя, найдём:

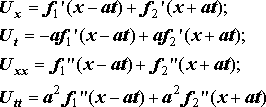
Отсюда следует, что равенство (1) выполняется, то есть функция U(x,t) является общим интегралом уравнения (1).

Задача состоит в том, чтобы, пользуясь начальными условиями (2), определить неизвестные функции f₁ и f₂.

П олагая в (3) t=0, найдём

( 4)

(5)

И нтегрируя второе равенство, получим:

,где х₀ и С- постоянные.

И з равенств

и

н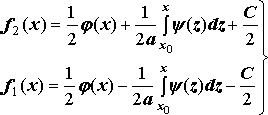 аходим:

(6)

З аменяя в формулах (6) аргумент х соответственно на x-at и x+at и подставляя полученное выражение в формулу (3), получим:

Таким образом, предположив существование решения задачи Коши, мы пришли к заключению, что оно должно представляться формулой (7). Следовательно, оно единственно (при заданных начальных условиях). Если j(х) обладает производными первого и второго порядка, а функция y(х)- производной первого порядка, то (7) даёт искомое решение задачи Коши (1)-(2). В этом можно убедиться непосредственной подстановкой правой части (7) в (1) и (2). Построив решение задачи Коши, мы, тем самым, доказали его существование.

Докажем устойчивость задачи Коши к малым изменениям начальных данных.

2. Теорема о непрерывной зависимости задачи Коши от начальных значений.

Теорема. Пусть U₁(x,t) и U₂(x,t) есть решения задачи Коши (1)-(2) с начальными условиями

Тогда каковы бы ни были e>0 и t₁>0, существует такое d>0, зависящее от e и t₁, что из неравенств

следует неравенство

,

то есть малым изменениям начальных условий соответствуют малые изменения решения задачи Коши.

Доказательство.

Используя формулу Даламбера, получим:

Следовательно

Е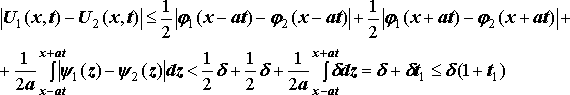 сли взять d=e/(t₁+1), то неравенство

, что и требовалось доказать.

Корректность задачи Коши для волнового уравнения.

Формулу Даламбера мы получили, предполагая существование решения поставленной задачи. Эта формула доказывает единственность решения. В самом деле, если существовало бы второе решение задачи Коши, то оно представлялось бы формулой:

и совпадало бы с первым решением.

Нетрудно проверить, что эта формула удовлетворяет (в предположении двукратной дифференцируемости функции j и однократной дифференцируемости функции y) уравнению и начальным условиям. Таким образом, изложенный метод доказывает как существование, так и единственность решения задачи Коши.

Выше было показано, что решение задачи Коши непрерывно зависит от исходных данных (устойчиво). Следовательно, задача Коши, рассмотренная нами, является корректно поставленной.

К некорректно поставленным задачам часто приводят обратные задачи математической физики: по некоторой информации о решении прямой задачи восстановить неизвестные физические величины, определяющие эту задачу ( источники, коэффициенты уравнения, краевые условия и так далее).

2. Обобщённое решение задачи Коши для непрерывных начальных данных.

Обратимся к задаче (1)-(2). Будем полагать, что начальные функции j(х) и y(х) ¹0 лишь на конечных отрезках, непрерывны всюду, а функция j(х) имеет производную первого порядка. Эти функции можно аппроксимировать дифференцируемыми функциями j_n(х) и y_n(х) так, что

, причём y_n(х) имеет первую производную, а j_n(х)- первую и вторую производные. Если в качестве начальных функций в задаче Коши взять функции j_n(х) и y_n(х), то они определяют единственное решение задачи U_n(x,t).

Оценим разность решений U_n+к(x,t)- U_n(x,t). В силу равномерной сходимости последовательностей {j_n(х)} и для {y_n(х)} для произвольных e>0 и t₁>0 найдётся такое N, что для любых n>N и любых целых положительных k будут выполняться неравенства:

д ля всех -¥<х<¥. Тогда по доказанной теореме для всех t³t₁ и -¥<х<¥ будут также выполняться неравенства:

Д ля любых n>N и любых целых положительных k. Но это означает, что последовательность решений {U_n(х,t)} равномерно сходится в указанной области к некоторой функции U(x,t). Эта функция называется обобщённым решением задачи Коши (1)-(2). При этом

или

Э та функция и её производная U_t(x,t) принимает заданные значения j(х) и y(х). Таким образом, в рассматриваемом случае формула Даламбера даёт обобщённое решение задачи Коши. Рассмотренную задачу можно решить иначе, если воспользоваться обобщёнными функциями и их свёртками.

2. Физическая интерпретация решения.

Решение (1)-(2) состоит из двух частей. Одна часть зависит от начального отклонения, вторая от начального импульса (скорости). Если

т о U=U₁+U₂.

Для выяснения физического смысла полученного решения рассмотрим сначала в отдельности функции, входящие в выражение: (3)

Н ачнём с функции f₁(x-at) и построим график этой функции при возрастающих значениях t: t=t₀, t=t₁, t=t₂ и т. д.

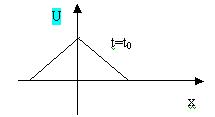
Второй график будет сдвинут на величину at₁ относительно первого, третий- на величину at₂ и так далее (мультфильм). При этом, если мысленно перемещаться вправо вдоль струны с постоянной скоростью а, то отклонение струны будет казаться всё время постоянным.

Процесс передвижения отклонения по струне называется волной.

Второе слагаемое- функция f₂(x+at) представляет собой волну, бегущую со скоростью а влево. Пусть движение происходит без начальной скорости, тогда

- полусумма прямой и обратной волн. Так как функция j(х)- известна, то мы можем вычислить значение U(x,t) для любых х и t. Прямые x-at=const и x+at=const являются характеристиками уравнения (1). Наглядное изображение описанного процесса можно получить, введя фазовую плоскость XOT. Рассмотрим плоскость (x,t) [плоскость состояний или фазовая плоскость]. Функция U=f(x-at) вдоль характеристики x-at=const сохраняет постоянное значение. Функция U=f(x+at) постоянна вдоль характеристики x-at=const. Рассмотрим распространение начального отклонения, заданного в виде равнобедренного треугольника на отрезке [a,b]. Построим на фазовой плоскости прямые x-at=a,b; x+at=a,b.

Эти прямые разобьют полуплоскость на 6 частей (зон). Колебание происходит только в тех точках и в те моменты времени, которые соответствуют зонам I, II, III. Точкам построенных прямых соответствуют положения переднего и заднего фронтов обеих волн.

#5