1. Уравнение гиперболического типа.

Уравнения с частными производными второго порядка гиперболического типа наиболее часто встречаются в физических задачах, связанных с процессами колебаний. Простейшее уравнение гиперболического типа

U_xx-U_yy=0

Обычно называют уравнением колебаний струны. Многие задачи механики ( колебания струн, стержней, мембран и трёхмерных объёмов) и физики (электромагнитные колебания) описываются уравнением:

где U(x,t)- неизвестная функция зависит от трёх пространственных координат х₁, х₂, х₃ и времени t; коэффициенты r, p и q определяются свойствами среды, где происходит колебательный процесс; свободный член F(x,t) выражает интенсивность внешнего возмущения. В последнем уравнении

П родемонстрируем вывод этого уравнения на примере малых поперечных колебаний струны.

2. Уравнение малых поперечных колебаний струны.

Пусть конечные точки струны закреплены, а струна туго натянута. Выведем струну из равновесия, и она начнёт колебаться. Будем предполагать, что все точки струны движутся перпендикулярно её положения равновесия (поперечные колебания), причём в каждый момент времени струна лежит в одной и той же плоскости.

- отк
лонение струны от положения равновесия; з
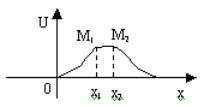
ависит от абсциссы точки струны х и от времени t. Нам требуется найти зависимость от х и t, то есть функцию U(x,t). При каждом фиксированном t график функции U(x,t) представляет форму колеблющейся струны в момент времени t (рис. 1), частная производная U_x(x,t) даёт при этом угловой коэффициент касательной в точке с абсциссой х. При изменении t форма струны меняется. При постоянном значении х функция U(x,t) даёт закон движения точки с абсциссой х вдоль прямой, параллельной оси OU, производная U_t(x,t)- скорость этого движения, U_t(x,t)- ускорение.

Задача состоит в том, чтобы составить уравнение, которому должна удовлетворять функция U(x,t). Будем предполагать, что:

1) струна абсолютно гибкая, то есть несопртивляющаяся изгибу (это значит, что если удалить часть струны, лежащую по одну сторону от какой-либо её точки, то сила натяжения Т, заменяющая действие удалённой части, будет всегда направлена по касательной к струне);

2) струна предполагается упругой и подчиняющейся закону Гука (изменение величины силы натяжения при этом пропорционально изменению длины струны);

3) струна однородна с линейной плотностью r.

Предположим, что на струну в плоскости колебания действуют силы, параллельные оси OU, которые могут меняться со временем и вдоль струны. Плотность распределения этих сил вдоль струны является функцией от x и t; обозначим её через g(x,t). В частности, если такая сила- вес струны, то g(x,t)=-rg (r- плотность, g- ускорение). Силами сопротивления среды, в которой происходят колебания, пока пренебрегаем.

У словие малости колебаний заключается в том, что величиной a²(x,t) можно пренебречь: a²»0,

(1)Так как

( 2) Далее (3)( 4)

Так как dU/dx=U_x=tga, то (U_x)²=0 (5)

Отсюда следует, что в процессе колебания мы можем пренебречь изменением длины любого участка струны, так как

( 6)

Покажем, что при сделанных предположениях, величину силы натяжения Т можно считать постоянной, не зависящей ни от точки её приложения, ни от времени t. Возьмём для этого участок струны M₁M₂ (рис. 3) в момент времени t и заменим действие отброшенных участков силами Т₁ и Т₂. Так как по условию все точки струны движутся параллельно оси OU и внешние силы также параллельны этой оси, то сумма проекций сил натяжения на ось OX должна равняться нулю:

, так как (7)

Отсюда в силу (3), Т₁=Т₂. В силу произвольности выбора точек М₁ и М₂ следует, что силы натяжения во всех точках равны между собой, то есть в пределах выбранной точности (в силу закона Гука) Т есть величина постоянная:

Т=Т₀ (8)

Вычислим сумму проекций сил Т₁ иТ₂ на ось OU. Выделим бесконечно малый участок струны с проекцией [x,x+dx] на ось абсцисс (рис. 4).

;

в силу (4)

, следовательно

( 9)

(здесь частное приращение производной ¶U/¶x заменено её частным дифференциалом (¶²U/¶x²)dx). Равнодействующую внешних сил, приложенных к участку М₁М₂ в момент времени t, обозначим через F. Согласно определению функции g(x,t)

( 10)

М асса участка М₁М₂ равна

Используя (9) и (10), получим (по второму закону Ньютона: произведение массы на ускорение равно сумме всех действующих сил):

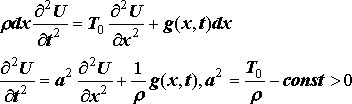( 11)

Уравнение (11) называется волновым уравнением (однородным) или уравнением колебаний струны. Это уравнение гиперболического типа.

Если g(x,t)=0, то уравнение однородное, оно описывает свободные колебания струны.

Если колебания происходят на плоскости, то

( 12)

Это уравнение описывает колебания мембраны. Если колебания происходят в пространстве, то

( 13)

Это уравнение описывает распространение звука в однородной среде.

Если силами сопротивления движению струны пренебречь нельзя, то в волновом уравнении необходимо учитывать член, пропорциональный скорости ¶U/¶t:

где r(x)- сила трения, которая пропорциональна скорости движения ¶U.

3. Уравнение Гельмгольца.

Рассмотрим волновое уравнение:

( 14)

Его решение будем искать в виде:

( 15)

Тогда

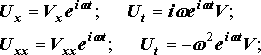( 16)

П осле подстановки получаем:

1 7)

,

(18)

(18)- уравнение Гельмгольца- одно из основных уравнений математической физики.

4. Начальные и граничные условия. Математическая постановка краевой задачи.

При решении задач физики или других областей науки математическими методами надо прежде всего дать математическую постановку задачи (математическую модель), а именно:

а) написать уравнение (или систему уравнений), которому удовлетворяет искомая функция (или система функций), описывающая исследуемое явление;

б) написать дополнительные условия, которым должна удовлетворять искомая функция на границах области её определения.

При этом следует убедиться:

1) в том, что дополнительные условия достаточны для выделения однозначного решения: это достигается доказательством теоремы единственности;

2) в том, что дополнительные условия не переопределяют задачу; это достигается доказательством теоремы существования; доказательство существования решения связано с методом нахождения решения;

3) в том, что малыми изменениями «исходных данных» задачи отвечают малые изменения решения; это свойство решения называется устойчивостью решения к малым изменениям «исходных данных».

В этом случае говорят, что математическая задача поставлена корректно.

Дифференциальные уравнения в частных производных второго порядка имеют бесчисленное множество решений, зависящих от двух произвольных функций.

Чтобы определить эти произвольные функции (выделить частное решение) нужно на искомую функцию, например, U(x,t) наложить дополнительное условие.

С аналогичным явлением мы встречались при решении дифференциальных уравнений, когда выделение частного решения из общего заключалось в процессе отсекания произвольных постоянных по заданным начальным условиям.

Если искомая функция описывает нестационарный процесс, то целесообразно за дополнительные условия взять величины, характеризующие эту функцию в какой- либо определённый момент времени. Этот момент обычно называют начальным. Кроме того, для характеристики искомой функции на границе области нужно знать граничные условия.

Для характеристики стационарных задач, где искомая функция не зависит от t, достаточно задать условия на границе. Граничные и начальные условия вместе называются краевыми условиями, а задача с такими условиями- краевой задачей.

5. Краевые задачи для уравнения колебаний струны.

Рассмотрим уравнение гиперболического типа (неоднородное):( 1)

Удобнее всего считать, что струна начала колебаться в момент времени t=0. Начальное положение точек струны (форма струны) задаётся условием:(2)

и начальная скорость:(3)

З апись означает, что функция U(x,t) взята при произвольном значении х и при t=0.

1) Иной характер имеют граничные условия. Они показывают, что происходит на концах струны во всё время колебания. В простейшем случае, когда концы струны жёстко закреплены (начало- в начале координат, а конец- в точке (l,0), функция U(x,t) будет подчиняться условиям:

( однородные граничные условия) (4)

Сформулируем задачу, к которой приводит изучение свободных колебаний струны, закреплённой на обеих концах.

Требуется решить неоднородное линейное дифференциальное уравнение с частными производными второго порядка с постоянными коэффициентами (1) при начальных условиях:

и краевых условиях:

Э то первая краевая задача с однородными граничными условиями.

Функции j(х) и y(х) определены на интервале [0,l] и j(0)=y(0)=0.

Если концы струны движутся по заданному закону, то граничные условия примут вид:

- первая краевая задача

m₁(t) m₂(t)- заданные функции времени t.

2) Если задаётся сила натяжения на концах, то мы имеем вторую краевую задачу. Так как Т(х)=kU_x, то на концах задаётся U_x:

Е сли натяжение отсутствует, то

- вторая краевая задача с однородными граничными условиями.

3) Характерным является условие упругого закрепления, например, для х=0

Е сли точка, (система) относительно которой имеет место упругое закрепление, перемещается и её отклонение от начального положения даётся функцией q(t), то граничные условия принимают вид:

или

Добавив сюда начальные условия:

, получим третью краевую задачу. Если q(t) или m₁(t)=m₂(t)=0, то имеем краевую задачу с однородными граничными условиями.

4) Если граничные условия при х=0 и х=l имеют различные типы, то такие краевые задачи называются смешанными.

5) Если нас интересует процесс в течение малого промежутка времени, когда влияние границ несущественно, то вместо полной задачи можно рассматривать предельную задачу с начальными условиями для неограниченной области.

Найти решение уравнения:

с начальными условиями

Э та задача называется задачей Коши.

#4